Das HKN-Projekt
Markus Lepper, 1978-2016

Inhalt
1          Einführung
2          Eigenschaften der vier dodekaphonen Modi und ihrer Reihungen
2.1          Die vier dodekaphonen Operationen und ihre Gruppenstruktur
2.2          Geeignete Ausgangsreihen und Symmetrieen
2.3          Zwölftonreihen aus Teilreihen
2.4          Folgen zweier Modi, Modi-Paare
2.5          Folgen aller Modi, All-Modi-Reihen
3          Exkurs: Die zwölftönigen All-Modi-Reihen
3.1          Mögliche Formen der Teilmengen
3.2          Konstruktion von Reihenabläufen
3.3          Beispiele in Noten für alle Zerlegungsformen
4          Minimale voll-modale musikalische Ausgangsgebilde, Haken
4.1          Konstruktion eines minimalen voll-modalen Materials
4.2          Doppelhaken
4.3          Hakenreihen
4.4          Optimierung der Anschlussintervalle in Hakenreihen
4.4.1          Maximierung der Anschlussintervalle
4.4.2          Minimierung der Anschlussintervalle
5          Historische Verwendung der aufgewiesenen Techniken und Materialien
6          Konstruktive Verwendung von Haken im voll-seriellen Kontext
6.1          Parameter-Polyphonie. Mögliche Kompositionsverfahren
6.2          Partiturbasierte Komposition von Hakenverläufen
6.3          Notation und Realisierung von Hakenverläufen mit tscore
6.4          Rein-Relative Abfolge der K-Ereignisse
6.5          Parameter-Interne Polyphonie. Mehr als drei V-Parameter-Stufen
6.6          Explizite Pausen und Gliederung
6.7          Doppelhaken
6.8          Mögliche Erweiterungen
7          Eine erste Studiensammlung "HKN_v00"
7.1          Konzept und Grundlegendes
7.2          Version "Vox" für Stimme Solo
7.3          Version "Vla" für Viola Solo
7.4          Version "Sig" für signalerzeugenden Synthesizer
7.5          Version "Svg" für bewegte Graphik
7.6          Generische Vorstudien
7.7          Erfahrungsbericht
7.8          Nice-to-haves, fehlende Implementierungsdetails
8          Historisches
         Bibliographie

(ausblenden)

^{^Inh} 1 Einführung

Das HKN-Projekt beschäftigt sich auf praktische und theoretische Weise mit zwei grundlegenden und eng zusammenhängenden Fragen der musikalischen Kompositionslehre im Zusammenhang mit den "vier Modi" der klassischen Zwölftontechnik (auch "Dodekaphonie" genannt).

Diese "vier Modi" einer gegebenen Zwölftonreihe (so der Sprachgebrauch der historisch etablierten Kompositionslehre) sind die Ausgangsreihe, ihr Inverses (auch "Umkehrung" genannt, ihr Retrograd (auch "Krebs" genannt) und ihr Retrograd-Inverses (auch "Krebsumkehrung"), im folgenden abgekürzt mit A, I, R und IR und weiter unten genauer spezifiziert.

Die Operationen, welche die gegebene Ausgangsgestalt A in diese anderen Modi transformieren, bezeichnen wir auch als A, I, R und IR und nennen sie "dodekaphone Operationen", oder im folgenden kurz "Operationen". Sie haben nämlich mit Schönbergs Formulierung der Dodekaphonie zum ersten Mal die Rolle einer fundamentalen, erstrangigen und tragenden materialgenerierenden Maßnahme erlangt. Allerdings waren sie in den Jahrhunderten davor durchaus bekannt; in Renaissance und Barock, die ja in einigen Unterepochen sehr wissenschaftsaffin und bastelfreudig waren, wurden sie manchmal gar exzessiv zu kompositorischen Virtuosenstücken herangezogen.

Wir bezeichnen als im engeren Sinne "voll-serielle Technik" die sich der Dodekaphonie methodisch und historisch anschließende Kompositionsweise, in der diese Behandlungsweise von Tonhöhen auf andere musikalische Parameter, ja letztlich auf beliebige Bestimmungsachsen übertragen wurde (bis hin zu Zeitungstexten und Farbabstufungen, siehe z.B. [lhuf not found]), -- oft auch auf Wertebereiche mit viel weniger als zwölf verschiedenen Stufen. Auch da spielen die dodekaphonen Operationen weiterhin eine fundamentale Rolle.

Der folgende Text wird für alle drei Epochen Beispiele bringen, um die praktische Relevanz unserer zunächst rein abstrakten Untersuchung zu demonstrieren. Diese beschäftigt sich mit der Frage, welche Eigenschaften ein "musikalisches Material", gesehen als "Folge von Werten in der Zeit", haben muss, damit alle vier Modi unterscheidbar sind. Diese Frage wird angewandt (a) auf Ausgangsreihen, die in sich bereits die Abfolge aller vier Modi einer zugrundeliegenden kürzeren Reihe ("Teilreihe") sind, und (b) zur Suche nach einem minimalen abstrakten Universal-Material.

Beide Fragen hängen eng zusammen, begründen gemeinsam die theoretischen und praktischen Aspekte des HKN-Projektes und können nachgewiesen werden als durchaus relevant in Werken von Bach über Webern bis in die Gegenwart. Die ursprüngliche Motivation zu dieser Untersuchung war eine Studienaufgabe seitens Prof. Hufschmidt im Wintersemester 1978/79 ausgehend vom Konzert op. 24 von Anton Webern, wie im folgenden genauer ausgeführt (siehe Kapitel 5, Abbildung 11 und Kapitel 8).

^{^Inh} 2 Eigenschaften der vier dodekaphonen Modi und ihrer Reihungen

^{^Inh} 2.1 Die vier dodekaphonen Operationen und ihre Gruppenstruktur

Eine genauere Definition der dodekaphonen Operationen ist wie folgt: Sei gegeben eine Ausgangsstruktur A. Diese ist eine geordnete endliche Liste von Werten aus einem gegebenen Wertebereich. Dieser ist endlich und diskret. Jedes Element einer solchen Liste, oder auch nur jede Indexposition im Zusammenhang einer bestimmten festgehaltenen Liste, heiße auch "Ereignis".

(Wir bezeichnen im folgenden die eigentlichen Operationen und das Ergebnis ihrer Anwendung auf ein gegebenes Material mit denselben Buchstaben, da eine Verwechslung im Kontext nicht möglich ist.)

Die Bildung des Retrograden R kann allgemein definiert werden durch die Umkehrung der Listen-Reihenfolge: es wird eine zweite Liste gebildet, und das erste Ereignis hier wird zum letzten Ereignis dort, das zweite Ereignis hier zum vorletzten Ereignis dort, etc.

Die Bildungs des Inversen I ist hingegen spezifisch für den Wertebereich: Es muss auf diesem (a) eine Ordnung definiert werden, und dann (b) eine injektive und totale Abbildung, die das laut dieser Ordnung höchstwertige Element auf das niederwertigste abbildet, das zweit-höchste auf das zweit-niedrigste, etc.
Man beachte weiterhin:
(c) Mit der Abbildung für I muss keinesfalls auch ein "Maß" definiert sein, d.h. diese Abbildungen können den Wertebereich beliebig "verzerren". So geschieht I bei Schönberg bezogen auf das äquidistant gegliederte chromatische Total, bei Bach hingegen auf eine diatonische Untermenge mit ungleichen Abständen ("Tonleiter").
(d) Die Abbildung für I stellt sich in den meisten Fällen am einfachsten dar als Spiegelung an einem ausgewählten Wert des Wertebereiches, resp. einer Lücke zwischen zwei benachbarten Werten.
(e) Jedwede injektive und totale Abbildung auf dem Wertebereich (also jede beliebige Permutation der Werte) kann eine ähnlich wirkende Operation auf der Ausgangsreihe A begründen. In der Tat wird dies im neueren Voll-Serialismus (in o.e. Bedeutung, siehe Kapitel 1) auch angewandt. Ja sogar nicht-injektive Abbildungen können musikalisch sinnvolle Transformationen ergeben. Jedoch gibt nur obige engere Regel die spezifische Situation der ursprünglichen historischen Entwicklung wieder, die hier Gegenstand der Untersuchung sein soll.

Bezeichne A auch die "Identische Operation", die also die Ausgangsgestalt A unverändert läßt. Laut (a) und (b) vertauscht die Abbildung für I jeweils zwei Elemente des Wertebereiches paarweise, und bildet ein eventuelles "mittleres Element" auf sich selbst ab. Die zweimalige Ausführung von I liefert also wieder die Ausgangsgestalt. Es gilt (mit der Hintereinanderschreibung als Hintereinanderausführung):
[invI] II=A
Daraus folgt unmittelbar
I(II) = IA = I = AI = (II)I
A und I bilden also eine zwei-elementige kommutative Gruppe mit A als neutralem Element und I als seinem eigenen Inversen.

All dies gilt auch für R, denn weil auch hier paarweise vertauscht wird, gilt auch hier
[invR] RR=A

Erlaubt man die kombinierte Anwendung von I und R auf ein Ausgangsmaterial, so ergibt sich eine mindestens vier-elementige Menge von Operationen, beginnend mit A, I, R, IR und RI. Diese nennen wir "G".

Es folgt zunächst aus den obigen Definitionen, dass dabei die Reihenfolge der Anwendung von I und R keine Auswirkungen haben kann: Die Reihenfolge in der Reihe (verändert von R) ist unabhängig von den Werten, und die Abbildung eines Wertes auf einen anderen (benutzt von I) ist unabhängig von der Position des Ereignisses in der Reihe. Also gilt
[kommIR] IR = RI

Gleichungen [invI], [invR] und [kommIR], sind die einzigen, die auf die Definition der Operationen und auf die Eigenschaften der enstehenden Gestalten bezugnehmen müssen. Die weiteren Gleichungen folgen daraus abstrakterweise, nämlich:
(IR)(IR) = I(RI)R = I(IR)R = (II)(RR) = AA = A
(IR)I = (RI)I = R(II) = R = (II)R = I(IR)
(IR)R = I(RR) = I = (RR)I = R(RI) = R(IR)

Jede beliebige Verkettung von Operationen aus G geht also nie über G hinaus, und G ist tatsächlich eine vier-elementige zusammengesetzte kommutative Gruppe mit folgender Tafel:

{A,I} und {A,R} und {A, IR} sind drei Untergruppen von G. Jeweils zwei davon determinieren die Gesamtgruppe vollständig. Üblicherweise wird bei der Konstruktion von G von I und R ausgegangen, da dies in der Definition der leztlichen Anwendung die grundlegenden Operationen sind, aber auch I und IR oder R und IR determinieren eindeutig G.
(Man vergleiche mit der "Gatter-Logik", wo zwar "Und" und "Nicht" die Grundoperationen sind, die technische Realisierung aber oft mit einem "Nand-Gatter" geschieht!-)

Die Operationen A, I, R und IR bilden aber nur dann eine derartige vier-elementige Gruppe, wenn das Material X, auf das die Operationen angewandt werden, auch für unterschiedliche Operationen auch tatsächlich unterscheidbare Ergebnisse liefert, wenn also gilt X != IX != RX != IRX. Ansonsten kollabiert die Gruppenstruktur. Dies wird im folgenden untersucht.

^{^Inh} 2.2 Geeignete Ausgangsreihen und Symmetrieen

Alle vier Operationen sind für kompositorisch-musikalische Zwecke offensichtlich nur dann sinnvoll, wenn die Ergebnisse ihrer Anwendung auf ein Ausgangsmaterial X jeweils unterscheidbar sind.

Die Unterscheidbarkeit zwischen dem Ausgangsmaterial X und dem Ergebnis der Anwendung einer Operation kann auch als Fehlen der entsprechenden Symmetrie beschrieben werden. Wir definieren:

Ein Ausgangsmaterial X ist I-(R-/IR-)symmetrisch, wenn die Anwendung der Operation I(R/IR) ein Ergebnis bringt, dass mit X identisch oder zumindest deckungsgleich ist. IR-Symmetrie heiße auch Punktsymmetrie. Wir schreiben diese Anwendung durch Voranstellen der Operation.

Umgekehrt: Ein Ausgangsmaterial X ist I-(R-/IR-)fähig, wenn es nicht I-(R-/IR-)symmetrisch ist.

So wie oben definiert konstituieren alle Operationen auf dem Ausgangsmaterial X allemal injektive Abbildungen, bilden also Gleiches auf Gleiches und Verschiedenes auf Verschiedenes ab. Es gilt also für jede Operation D und Materialien X und Y
[transEq] X=Y => DX=DY
[transNonEq] X!=Y => DX!=DY

Deshalb sind Symmetrieen und Unsymmetrieen nicht von einander unabhängig, sondern vererben sich auf alle Modi des Ausgangsmateriales. (Z.B. wenn eine Tonfolge X R-symmetrisch ist, sind auch all ihre Modi RX, IX und IRX ebenfalls R-symmetrisch.)

Ein Ausgangsmaterial X heiße voll-modal, wenn es weder I- noch R- noch IR-symmetrisch ist.

Es gilt also
[vollModal] AX != IRX und AX != RX und AX != IX

Seien B und C zwei beliebige aber verschiedene Operationen. Zunächst gilt ganz allgemein gruppentheoretisch, also bereits im Sinne des vorangehenden Abschnittes,
[x1] CB != A,
denn sonst folgte widersprüchlicherweise
CB=A ==> CCB=CA ==> B=C.

Bei voll-modalem X folgt, dass die durch B und C enstehenden Modi stets unterschiedlich sind, also
BX!=CX
denn sonst folgte der Widerspruch
BX = CX ==> BBX = CBX ==> AX = CBX
denn CB muss nach [x1] eines von I, R oder IR sein, und die letzte Gleichung widerspricht damit [vollModal].

Seien B und C zwei untereinander und von A verschiedener Operationen. Hat ein Material X eine einzige Symmetrie bezgl. B, dann braucht es deshalb keine weiteren zu haben, also
BX=X und CX!=X und BCX!=X
ist widerspruchsfrei. (Die Tonhöhenfolge c-d-c ist R-symmetrisch, aber nicht I- und IR-symmetrisch.)

Gelten aber zwei verschiedene Symmetrieen bezgl. B und C , so gilt auch die dritte bezgl. CB:
[nonZwei] (BX=X und CX=X) ==> (CBX=CX und CX=X) ==> CBX=X

Liegt ein System von Gleichheits- und Ungleichheitsaussagen über die Modi eines Ausgangsmaterials vor, so kann dieses wegen [transEq] und [transNonEq] normiert werden, bis auf der linken Seite nur X erscheint. (Wir verwenden die Terme "A", "X" und "AX" austauschbar, sie meinen stets die identische Abbildung und/oder das unveränderte Ausgangsmaterial.) Diesem Zustand kann dann Eindeutigkeit und Widersprüchlichkeit sofort abgelesen werden.

Z.B.:
{ RI=I und A!=I und R=I und R!=RI }
==>
{ RIRI=IRI und A!=I und RR=IR und RR!=RIR }
==>
{ A=IIR und A!=I und A=IR und A!=RRI }
==>
{ A=R und A!=I und A=IR und A!=I }
Diese Forderungssystem ist unerfüllbar, denn genau zwei Symmetrieen sind nach [nonZwei] nicht möglich.

{ RI=R und R!=I }
==>
{ RIRI=RRI und RR!=IR }
==>
{ A=I und A!=IR }
Diese Forderungssystem ist erfüllbar und eindeutig, denn es gilt zusätzlich A!=R, wiederum wegen [nonZwei].

In der historischen Praxis gibt es nun interessante Unsymmetrieen, was diese Symmetrieen betrifft. Es gilt:
Eine einstimmige Folge von Tonhöhen (oder anderen Werten), die mindestens einen Schritt macht, ist niemals I-symmetrisch, kann aber R-symmetrisch sein.

Wenn nämlich zwischen zwei benachbarten Ereignissen in A ein Schritt aufwärts geschieht, geschieht in I ein Schritt abwärts.

Bei komplexeren Abbildungen im Wertebereich W, z.B. modulo Oktave, oder nicht-surjektiven, kann das Ergebnis aber anders sein. Dies sind aber Ausnahmefälle, die nicht dem hier untersuchten historischen Normalfall entsprechen. ((FIXME Genaueres fehlt!!))

Dies ändert sich erst bei mehr-stimmigen Verläufen, wo nämlich die eine Stimme deckungsgleich auf die andere abgebildet werden kann. Ein wichtiges Beispiel ist die tonale Kadenz. Folgender Verlauf ist I-, R- und IR-symmetrisch, und jede zweistellige Unterfolge daraus ist I-symmetrisch:

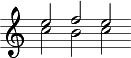
Abbildung 2: Die Oberstimmen einer Kadenz und ihre Symmetrieeigenschaften

Die Ober- und Unterstimme aus voranstehendem Beispiel sind jeweils R-symmetrisch. R-symmetrische Tonhöhenfolgen sind möglich, falls Tonhöhen wiederholt auftreten dürfen. Nur dann ist es nämlich möglich, dass durch die Umkehrung der Reihenfolge identische Tonhöhen aufeinanderfallen.

Das Wiederholungsverbot bei Schönberg hat also die für seine Zwecke nützliche Konsequenz, das R-Symmetrieen ausgeschlossen werden, dass die Reihen immer R-fähig sind.

Oben angeführte I-Symmetrie beruht ja auch auf einer Wiederholung: ein zweistimmiger Verlauf ist ja nur möglich, wenn in seiner Darstellung als "Relation Listenposition zu Tonhöhe" eine Listenposition mehr als einmal verwendet wird, also "wiederholt" wird.

^{^Inh} 2.3 Zwölftonreihen aus Teilreihen

In der historischen Entwicklung der Dodekaphonie stellte es sich bald heraus, dass in bestimmten Satz- und Verwendungszusammenhängen eine Zwölftonreihe als Ganze schlecht zu rezipieren ist, also wenig Wiedererkennbarkeit und formale Bildungskraft hat. Ein Mittel dagegen ist, eine Zwölftonreihe aus gut erkennbaren Unterabschnitten aufzubauen. Diese nennen wir Teilreihen.

Teilreihen können durchaus verschiedenartige Struktur und Funktion haben, wie z.B.

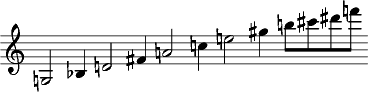
Abbildung 3: Struktur der Reihe aus Bergs Violinkonzert

die Reihe aus Alban Bergs Violinkonzert, ein besonders prägnantes Beispiel.

Hier sind die Teilreihen sogar in einander verschränkt und haben durchaus unterschiedlichen Aufbau, Semantik, Funktion und historisches Herkommen:

1. Die leeren Saiten des Solo-Instrumentes (dargestellt als Halbe Noten).
2. Vier Dreiklänge auf diesen Seiten, abwechselnd moll und Dur (Halbe plus Viertel).
3. Die Ganztonleiter des Choral-Beginnes "Es ist genung" (Achtelnoten).

(Der Choral, der mit der Ganztonleiter beginnt, wird am Ende bekanntlich zitiert und ausgiebig durchgeführt. In diesem Kontext muss der letzte Ton als "eis" geschrieben werden, eine Notationsweise, die in der orthodoxen Dodekaphonie völlig tabu ist, und mit der der Komponist den Lehrer vielleicht gar provozieren wollte ?-)

Vorliegende Untersuchung beschäftigt sich aber mit genau dem gegenteiligen Fall, dass nämlich die Teilreihen möglichst ähnlich sind, weil sie ihrerseits schon durch die dodekaphonen Operationen aus einander hervorgehen.

^{^Inh} 2.4 Folgen zweier Modi, Modi-Paare

Im Zentrum dieser Untersuchung steht zum einen die Frage, wie sich eine Reihe verhält, insbesondere eine Zwölftonreihe, die aus einer Abfolge von Teilreihen besteht, die verschiedene Modi desselben Ausgangsmaterials sind. Anders gefragt: Wie sich die internen Modi-Operationen zwischen solchen Teilreihen auf die Operationen auf der Gesamtreihe auswirken.
Für diese Frage gibt es historische Beispiele, später im Text ausführlich vorgestellt, die ihre kompositionsgeschichtliche Relevanz nicht zuletzt aus den Mechanismen beziehen, die bei der konkreten Wahrnehmung derartiger Gestalten wirksam werden.

Gehen wir also zunächst davon aus, dass wir eine kurze Wertefolge "A" gefunden hätten, die voll-modal ist. (Die Frage nach einer minimalen solchen Folge ist die zweite Teilfrage dieser Untersuchung, siehe Kapitel 4.) Konstruieren wir nun die Reihen, die Folgen von Modi von Teilreihen sind, "bottom-up", beginnen also mit Paaren aus zwei verschiedenen Modi der Ausgangsgestalt A. Diese nennen wir ein Modi-Paar.

Zunächst fragen wir, welche Symmetrieen durch diese Paarbildung neu entstehen können. Dabei notieren wir die zeitliche Aufeinanderfolge mit einem Semikolon als "_;_". Setzen wir A als erstes Segment, gefolgt von einem zweiten, von A verschiedenen Modus, so entspricht diese Frage der Auflösung nach "x" in den folgenden Gleichungen:
[Symm2I] I(A;x) = A;x
[Symm2R] R(A;x) = A;x
[Symm2IR] IR(A;x) = A;x

Im ersten Fall gilt, dass die I Operation über das Semikolon distributiert, da sie ja nur auf Werten definiert ist und die Position in der Reihe keine Rolle spielt. [Symm2I] geht also über in
(I(A;x) = IA;Ix = A;x) ==> (IA=A und Ix=x)

Da aber A voll-modal sein soll, ist schon die erste Teilbedingung der abschließenden Disjunktion unerfüllbar. Eine Hintereinandersetzung zweier beliebiger Modi einer nicht-I-symmetrischen Folge ist also niemals I-symmetrisch.

Ist dieses Ergebnis noch trivial, so wird es nun interessanter. Bezeichen "P(_;_)" die "Permutation" der durch das Semikolon verbundenen Terme. Die Operation R distributiert nämlich nicht über das Semikolon, sondern bewirkt zusätzlich diese Permutation. Es gilt also
R(b;c) = P(Rb; Rc) = Rc;Rb
und entsprechend
IR(b;c) = I(P(Rb; Rc)) = I(Rc;Rb) = IRc;IRb

[Symm2R] geht damit über in
(R(A;x) = P(RA;Rx) = Rx;RA = A;x) ==> (Rx=A und RA=x)
Die beiden Gleichungen der Disjunktion sind gleichbedeutend, und eingesetzt ergibt sich die Symmetriegleichung
[Symm2R'] R(A;R) = A;R

Die Folge von Ausgangsform und Retrograd ist also retrograd-symmetrisch.

[Symm2IR] geht über in
(IR(A;x) = P(IRA;IRx) = IRx;IRA = A;x) ==> (IRx=A und IRA=x)
Die beiden Gleichungen der Disjunktion sind wieder gleichbedeutend, es folgt
[Symm2IR'] IR(A;IR) = A;IR

Die Folge von Ausgangsform und IR ist also punktsymmetrisch.

^{^Inh} 2.5 Folgen aller Modi, All-Modi-Reihen

Zusammengefasst als Tabelle [T4symm] ;

^{^Inh} 3 Exkurs: Die zwölftönigen All-Modi-Reihen

^{^Inh} 3.1 Mögliche Formen der Teilmengen

Welche Möglichkeiten bestehen nun für All-Modi-Reihen im Kontext der "klassischen Dodekaphonie", wenn also alle vier(4) Modi der Teilreihe zusammen eine Zwölftonreihe ergeben sollen? Denn immerhin war ja genau dieser Befund in Anton Weberns Konzert op.24 ja die Motivation zu dieser Untersuchung, siehe Kapitel 5.
Selbstverständlich enthält jede der Teilreihen genau drei(3) Tonklassen, weil 12/4=3. (Wir reden im Rest des Abschnittes auch einfach von "Tonhöhen" oder "Tönen".) Die vier Modi werden in derartigen Setzungen gegebenenfalls zusätzlich noch transponiert, eine Maßnahme, die im Rest des Artikels überhaupt nicht besprochen wird, da dieser ja nur von "abstrakten" Haken handelt, nur von der Kontur. Auch im folgenden soll solch eine Transposition nur als "notwendiges Übel" aufgefasst werden und beliebig realisierbar sein. In der Tat setzt ja die Konstruktion des Inversen (Operation I) immer schon die Festlegung der Spiegelachse im Wertebereich voraus. Sie beinhaltet also zwangsläufigerweise eine Transposition, ist ohne eine solche garnicht definierbar. Nur bei reinem "R" könnten die Tonhöhen beibehalten werden und müssen nun, da die All-Modi-Reihe in sich ja wieder eine Zwölftonreihe sein soll, also dem Wiederholungsverbot unterliegt, zusätzlich und nach Notwendigkeit transponiert werden.

Konstruieren wir zunächst die Intervallstrukturen der bloßen Tonklassenmengen für alle vier Modi, also unter Abstraktion von der Reihenfolge der Anordnung drei Töne in den einzelnen Modi. Dann ist klar dass die Tonklassenmengen von A und R deckungsgleich sein müssen, also identisch modulo Transposition. Ebenso die von I und IR. Die Tonklassenmengen von A und R sind deckungsgleich mit den Umkehrungen der Tonklassenmengen von I und IR.

Seien im folgenden a, b, c und d diese vier Tonklassenmengen, mit a für die Ausgangsgestalt, b für I (oder IR), c für R und d für IR (oder I).
(Darüberhinaus können die Tonklassenmengen in sich symmetrisch sein, sodass alle vier Mengen deckungsgleich sind und die Modi A, I, R und IR beliebig auf sie verteilt werden können. Nur der einfacheren sprachlichen Benennung wegen gehen wir zunächst davon aus, dass das nicht der Fall ist, also die Zuordnungen c=R und b/d = I/IR zwingend sind.)

[alleDisj] alle Paare aus {a,b,c,d} sind disjunkt.

Es bestehen also vier Symmetrieachsen s1, s2, s3 und s4 und folgende Gleichungen, wobei "x.s1" für die Anwendung der Spiegelung an der Achse s1 (resp. der dadurch definierten Abbildung) auf ein x stehe:

[defb] a.s1 = b
[defc] b.s2 = c = a.s1.s2
[defd] c.s3 = d = a.s1.s2.s3
[defCirc] d.s4 = a = a.s1.s2.s3.s4

Über die gegenseitige Lage der Spiegelachsen wissen wir zunächst nichts. Nur, dass wegen [alleDisj] gilt:
[SpiegelNonEq] s1!=s2 und s2!=s3 und s3!=s4 und s4!=s1

Versuchen wir nun, eine dodekaphone All-Modi-Reihe zu konstruieren. Bestimmen wir dazu als erstes vier Tonklassen, die durch die sukzessive Anwendung der Spiegelungen auseinander hervorgehen sollen, also a1 aus der Menge a, b1=a1.s1 aus b, c1=a1.s1.s2 aus c und d1=a1.s1.s2.s3 aus d. Eine solche Abfolge nennen wir auch Viererzyklus und schreiben
V1 = <a1, b1, c1, d1>,
und so auch für V2 und V3.
Die Menge der vier Töne eines Zyklus, also ohne Ansehung der Reihenfolge, heiße Vierermenge, als W1, W2, W3 entsprechend.

Diese vier Tonklassen können zunächst völlig beliebig gesetzt werden und bestimmen damit implizit die vier Spiegelachsen. Gibt es für diese Setzung zwingend notwendige Einschränkungen?

Wenn wir danach nämlich den zweiten Ton "a2" aus a setzen wollen, so darf weder er selber noch einer seiner Spiegelungen mit einem bereits gesetzten Ton zusammenfallen, V1 und V2 müssen disjunkt sein, -- wir wollen ja eine "Zwölftonreihe mit Wiederholungsverbot" bauen. Rein schematisch ergeben sich 16 Ungleichungen, die aber nicht alle neues beitragen. Sie lauten:

[neq00] a2 != a1
[neq01] a2 != a1.s1 = b1
[neq02] a2 != a1.s1.s2 = c1
[neq03] a2 != a1.s1.s2.s3 = d1
[----] a2.s1 != a1 <==> a2 != a1.s1 [=neq1]
[----] a2.s1 != a1.s1 <==> a2 != a1 [=neq0]
[neq12] a2.s1 != a1.s1.s2 <==> a2 != a1.s1.s2.s1
[neq13] a2.s1 != a1.s1.s2.s3 <==> a2 != a1.s1.s2.s3.s1
[neq20] a2.s1.s2 != a1 <==> a2 != a1.s2.s1
[----] a2.s1.s2 != a1.s1 <==> a2 != a1.s1.s2.s1 [=neq12]
[----] a2.s1.s2 != a1.s1.s2 <==> a2 != a1 [=neq00]
[neq23] a2.s1.s2 != a1.s1.s2.s3 <==> a2 != a1.s1.s2.s3.s2.s1
[neq30] a2.s1.s2.s3 != a1 <==> a2 != a1.s3.s2.s1
[neq31] a2.s1.s2.s3 != a1.s1 <==> a2 != a1.s1.s3.s2.s1
[----] a2.s1.s2.s3 != a1.s1.s2 <==> a2.s1.s2 != a1.s1.s2.s3 [=neq23]
[----] a2.s1.s2.s3 != a1.s1.s2.s3 <==> a2=a1 [neq00]

Die Umformungen basieren auf den Rechenregeln
x.s.s = x
(=Jede Spiegelung ist ihre eigene Umkehrung.)
x = y <=> x.s = y.s
x != y <=> x.s != y.s
(=Spiegelungen sind bijektiv und bilden gleiches auf gleiches und verschiedenes auf verschiedenes ab.)

Es gibt also zehn(10) Terme, die a2 nicht annehmen darf. Ist a2 einmal gesetzt, dann bestehen für a3 also zwanzig(20) derartiger Verbote. Diese können diese offensichtlich nicht alle verschieden sein, da es ja insgesamt nur 12 Tonhöhen gibt. Nur diese Beschränkung der Grundmenge ermöglicht überhaupt weitere Folgerungen über die Lage der Symmetrieachsen.

Die rechten Seiten von [neq00] bis [neq03] sind laut Voraussetzung [alleDisj] alle verschieden.

Wir können also diese und die rechten Seiten von [neq12] bis [neq31] gleichsetzen, und deren Kombinatinen untereinander. Dabei benutzen wir als zusätzliche Rechenregel
x.sy = x.sz <==> sy = sz
Diese folgt aus der besonderen Konstellation, dass die Spiegelachsen sich ja nur im Mittelpunkt des Kreises schneiden, die Töne aber nie dort, sondern nur auf dem Umfang liegen.

[neq12=00] a1.s1.s2.s1 = a1 <==> a1.s1.s2 = a1.s1 <==> c1=b1 ist unerfüllbar.
[neq12=01] a1.s1.s2.s1 = a1.s1 <==> a1.s1.s2 = a1 <==> c1=a1 ist unerfüllbar.
[neq12=02] a1.s1.s2.s1 = a1.s1.s2 <==> a1.s1.s2 in s1, scheint erstmal erfüllbar.
[neq12=01] a1.s1.s2.s1 = a1.s1.s2.s3 <==> s1=s3, erstmal erfüllbar.

[neq13=00] a1.s1.s2.s3.s1 = a1 <==> a1.s1.s2.s3 = a1.s1 <==> d1=b1 ist unerfüllbar.
[neq13=01] a1.s1.s2.s3.s1 = a1.s1 <==> a1.s1.s2.s3 = a1 <==> d1=a1 ist unerfüllbar.
[neq13=02] a1.s1.s2.s3.s1 = a1.s1.s2 <==> d1.s1 = c1, scheint erstmal erfüllbar.
[neq13=01] a1.s1.s2.s3.s1 = a1.s1.s2.s3 <==> d1 in s1 erstmal erfüllbar.

[neq20=00] a1.s2.s1 = a1 <==> a1.s2 = a1.s1 <==> s2=s1 nicht erfüllbar wegen [SpiegelNonEq].
[neq20=01] a1.s2.s1 = a1.s1 <==> a1.s2 = a1 nicht erfüllbar wegen [alleDisj].
[neq20=02] a1.s2.s1 = a1.s1.s2 <==> a1 = a1.s1.s2.s1.s2 <==> (s1.s2) ist Drehung um ganzen Kreis oder null <==> s1 orthogonal zu s2
[neq20=01] a1.s2.s1 = a1.s1.s2.s3 <==> a1 in s3 (scheint erstmal erfüllbar)

[neq23=00] a1.s1.s2.s3.s2.s1 = a1 <==> a1.s1.s2.s3 = a1.s1.s2 <==> d1=c1 falsch wegen [alleDisj]
[neq23=01] a1.s1.s2.s3.s2.s1 = a1.s1 <==> a1.s1.s2.s3 = a1.s2 <==> d1=b1 falsch wegen [alleDisj]
[neq23=02] a1.s1.s2.s3.s2.s1 = a1.s1.s2 (scheint erstmal erfüllbar)
[neq23=03] a1.s1.s2.s3.s2.s1 = a1.s1.s2.s3 (scheint erstmal erfüllbar) a

XXX FIXME GENAUER / alle ausprobieren !?!?
Um die restliche Seiten zu vereinheitlichen ist es am einfachsten, zwei Spiegelachsen gleichzusetzen. Von den in den obigen Schreibweisen auftretenden können laut [SpiegelNonEq] dies nur s1 und s3 sein:
[equ13] s3=s1.

Daraus ergeben sich sofort wichtige Folgerungen:
Die Konstruktionsregeln [defb] bis [defd] geben an, welche Mengen an welchen Achsen gespiegelt werden. Mit [equ13] bedeuten sie nun, dass in jedem Viererzyklus jeder Ton auf genau einer Seite an der Achse s1 auf seinen Nachbarton gespiegelt wird. (Die jeweils andere Seite bleibt s2 oder s4, wie oben festgelegt.)

[defCirc] geht über in:
a = a.s1.s2.s1.s4 = a.(s1.s2).(s1.s4)

Die Verknüpfung zweier Spiegelungen an sich schneidenden Achsen ist bekanntlich eine Drehung um das Doppelte des von ihnen eingeschlossenen Winkels. (s1.s2) und (s1.s4) sind also Drehungen, die sich aufheben. Folglich gilt:

[SpiegelSymm24] s2 und s4 liegen auf verschiedenen Seiten von s1 im Abstand desselben Winkels, also symmetrisch zu s1.

Dies wird auch ausgedrückt als
[Umk24] x.s4 = x.s1.s2.s1

Weiterhin folgt:
[S1Virtuell] Die Spiegelachse s1 (bildet a auf b ab, und c auf d) ist "virtuell" (sie liegt zwischen zwei Tönen) und nicht "materiell" (liegt auf einem Ton).
Begründung: Eine materielle Spiegelachse bildet den Ton, durch den sie geht, auf diesen selbst ab. Da s1 aber im Rahmen der Konstruktion nun sämtliche Töne auf einen Nachbarn aus einer disjunkten Menge abbildet [alleDisj], kann s1 nicht materiell sein.

Nennen wir "Achsenton" den Ton, durch den eine materielle Spiegelachse geht. Dann gilt;
[S24Mat] Die Spiegelachse s2 (bildet Menge b auf c ab) kann materiell sein, mit Achsentönen aus a und/oder d. Genau dann ist wg. [SpiegelSymm24] auch s4 (bildet d auf a ab) auch materiell, mit Achsentönen aus b und/oder c.

Im Gegensatz zur ursprünglichen Annahme können also die ersten Töne nicht beliebig gesetzt werden, sondern müssen, wenn wir [equ13] als notwendig annehmen FIXME NACHWEIS, die Regeln [equ13], [SpiegelSymm24] und [S1Virtuell] beachten, um zu einer vollständigen Zerlegung zu kommen, die [defb] bis [defd] erfüllt.

Wenn [equ13] in obige Ungleichungen eingesetzt wird, kollabieren die rechten Seiten von [neq12] bis [neq31], also die für a2 "verbotenen" Töne jenseits von V1, zu:

[neq12] a2 != a1.s1.s2.s1 = a1.s1.s2.s3 = d1 [=neq03]
[neq13] a2 != a1.s1.s2.s1.s1 = a1.s1.s2 = c1 [=neq02]
[neq20] a2 != a1.s2.s1
[neq23] a2 != a1.s1.s2.s1.s2.s1 (= a1.s4.s2.s1)

[neq30] a2 != a1.s3.s2.s1 = a1.s1.s2.s3 = d1 [=neq03]
[neq31] a2 != a1.s1.s1.s2.s1 = a1.s2.s1 [=neq20]

Alle für a2 verbotenen Positionen zeigt folgende Graphik:

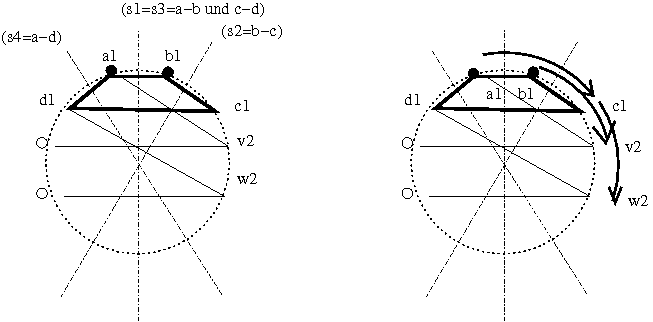
[neq00] bis [neq03] sagen trivialerweise ja nur, dass a2 nicht direkt auf einen Ton aus V1 gesetzt werden kann. Ergiebiger für die weitere Konstruktion können [neq20] und [neq23] sein, weil sie evtl. über diese Menge hinausgehen.
Eine mögliche anschauliche Interpretation ergibt sich durch folgende Umformung:
a2 != a1.s2.s1 <==> a2.s1=b2 != a1.s2=v2 [aus neq20]
a2 != a1.s1.s2.s1.s2.s1 <==> a2.s1=b2 != d1.s2=w2 [aus neq23]

b2 darf also weder auf v2 noch auf w2 fallen.
(
Für c2 gilt dasselbe:
a2 != c1 <==> a2.s1.s2 != c1.s1.s2 <==> c2 != d1.s2=w2 [aus neq02]
a2 != b1 <==> a2.s1.s2 != b1.s1.s2 <==> c2 != a1.s2=v2 [aus neq01]
)

Die Töne/Positionen b und c werden ja in jeder Vierermenge an der Achse s2 gepiegelt. w2 und v2 aber würden an s2 gespiegelt einen Ton aus W1 wiederholen. Sie können also nur mit ihren Spiegelbildern an der Achse s4 in W2/W3 enthalten sein, also auf den Positionen a und d.

Zunächst aber ist zu untersuchen, ob v2 und w2 überhaupt über W1 hinausgehen. Dazu sind acht Ungleichungen zu lösen:
[SMat-a] v2 = a1.s2 ?= a1 [scheint erfüllbar]
v2 = a1.s2 != b1 = a1.s1 <== [SpiegelNonEq]
und ausserdem liegt kein Ton auf zwei Spiegelachse zugleich.
v2 = a1.s2 != c1 = a1.s1.s2 <==> a1 != a1.s1 <== [alleDisj]
[equ24p] v2 = a1.s2 ?= d1 = a1.s1.s2.s1 <==> a1.s2.s1 ?= a1.s1.s2 [scheint erfüllbar]

[equ24p] w2 = d1.s2 = a1.s4.s2 != a1 <==> a1.s4 != a1.s2 <==> a1.s1.s2.s1 != a1.s2 <==> a1.s1.s2 != a1.s2.s1
w2 = d1.s2 != b1 <==> d1 != b1.s2 = c1 <== [alleDisj]
w2 = d1.s2 != c1 = d1.s1 <== [SpiegelNonEq]
[SMat-d] w2 = d1.s2 ?= d1 [scheint erfüllbar]

Nur [SMat-a], [SMat-d] und [eq24p] scheinen als Gleichungen erfüllbar, die andere sind als Ungleichungen ableitbar. Dies zeigt gleich zwei wichtige Grenzfälle:

Erster Sonderfall:
[equ24] a1.s2.s1 = a1.s1.s2 <==> a1.s2.s1.s2.s1 = a1 <==> a1.(s2.s1).(s2.s1) = a1

Die Spiegelung an zwei sich schneidenden Achsen ist bekanntlich eine Rotation um das Doppelte ihres Winkels. Die durch (s2.s1) erzeugte Rotation ist also die um einen Halbkreis, und der Winkel zwischen s2 und s1 ist folglich ein Viertelkreis. Also stehen s1 und s2 orthogonal zu einander, und wegen [SpiegelSymm24] fallen s2 und s4 zusammen. Für den charakteristischen Winkel s2-s1 gilt
alpha = 3
FIXME einführen alpha und bogenmaß !!
Ausserdem
[equ24] s2 = s4

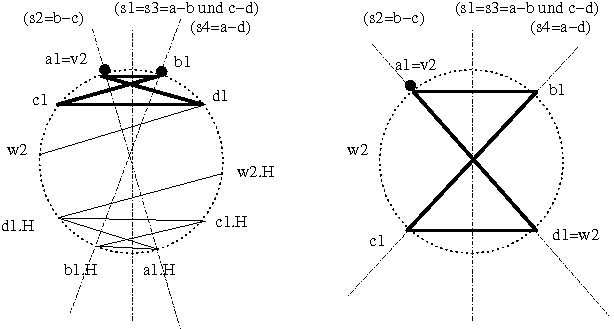
In diesem Falle können die Rollen a bis d beliebig allen vier Positionen zugeordnet werden, da ja die Achsen s2 und s4 zusammenfallen. Dies zeigt folgende Abbildung:

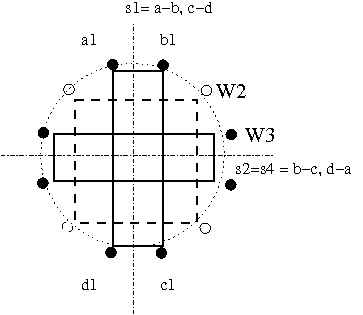
Wir setzen a1 beliebig auf "elf Uhr". Für W2 und W3 gibt es dann je vier mögliche Viererzyklen, entsprechend den vier Möglichkeiten für a2 und a3.

FIXME ROTATIONSSYMMETRISCHE rausnehmen !?!?

Hingegen [SMat-a] bedeutet, dass s2 eine materielle Spiegelachse ist, die durch den Ton a1 geht. Nur dann gilt a1.s2=v2=a1. Wegen [SpiegelSymm24] ist dann s4 ebenfalls materiell und geht durch b1.
[SMat-d] bedeutet, dass s2 durch den Ton d1 geht und s4 durch c1.

Da die reine Benennung der Mengen als "a, b, c, d" nichts zur Struktur beiträgt, können wir in V1 diese beliebig vornehmen und uns also auf den Fall [SMat-a] beschränken.

In diesem Fall gilt [equ24] selbstverständlich nicht, denn s4 darf nicht durch a1 gehen, wegen [alleDisj]. (Überhaupt ist im Falle [equ24] die Achse s2=s4 als eine zu s1 orthogonale ebenfalls virtuell und nicht materiell.)

Wenn nun ausserdem noch [SMat-d] gilt, heisst das, dass s2 durch a1 und d1 zugleich geht. (Und damit s4 durch b1 und c1.)
Dann liegen a1 und d1=a1.s4=a1.s2.s4 also einen halben Kreisumfang entfernt, der Winkel zwischen s2 und s4 ist ein Viertelkreis, und wegen [SpiegelSymm24] der zwischen s1 und s2 (oder s4) ein Achtelkreis =1.5 im Bogenmaß. FIXME EINFÜHREN (Siehe unten, rechte Abbildung.)
Damit bleiben v2 und w2 in W1, und für die nächste Menge ergibt sich aus diesen keine Einschränkung.

FIXME WEITERKONSTRUIEREN

XXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXx

Bezeichne
x.H
die um einen Halbkreis gedrehte Position x.

Ist der Winkel alpha != 1.5 und gilt [SMat-a], dann gilt also [SMat-d] nicht, und w2=d1.s2 liegt nicht in W1, bildet also weiterhin ein Ausschlusskriterium für die weitere Konstruktion.
Darüberhinaus liegen bei a1.H in s2 und b1.H in s4 ebenfalls Achsentöne, die nicht in W1 liegen. Diese müssen an der jeweils anderen Achse gespiegelt werden. Damit ist eine zweite Vierermenge eindeutig festgelegt:
W2 = {a1.H, a1.H.s1=b1.H, a1.H.s1.s2=c1.H, a1.H.s1.s2.s1=d1.H}
Da a1.H nur an s4 gespiegelt werden kann, gilt das auch für a1.H.s4, und diese müssen auf Positionen a und d stehen. Es gibt also zwei Viererzyklen, die zwei Durchlaufsinne durch die Menge darstellen:
V2a = < a1.H, a1.H.s1=b1.H, a1.H.s1.s2=c1.H, a1.H.s1.s2.s1=d1.H=a1.H.s4 >
V2b = < a1.H.s4, a1.H.s1.s2, a1.H.s1, a1.H >

w2.H ist deshalb ebenfalls ein potentielles weiteres Ausschlusskriterium, wie w2. Das aber nur wenn gilt (w2 !in W2), gleichbedeutend mit (w2.H !in W1), siehe folgende Abbildung.

Ersteres ist äquivalent mit folgenden vier Ungleichungen:
w2=d1.s2 != a1.H
Gilt, denn a1 in s2 ==> a1.H in s2, aber d1 !in s2 ==> d1.s2 !in s2.
w2=d1.s2 != a1.s1.H=b1.H
Gilt, denn b1 in s4 ==> b1.H in s4, aber ????
w2=d1.s2 != a1.s1.s2.H=c1.H

d1.s2 != d1.H

FIXME w2 !in W2 ?? w2.H !in W1 ?????
Deshalb bleiben vier Töne übrig, die nur auf zwei verschiedene Weise den Mengen a bis d zugeordnet werden, also zwei weitere Zyklen V3a und V3b, die allerdings mit V2a und V2b frei kombinierbar sind.
Der Sonderfall [SMat-a] führt also zu vier verschiedenen Zerlegungen.

XXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXx
In diesem liegt auf den anderen Enden der Achsen ebenfalls je ein Achsenton. Diese induzieren sofort eindeutig eine zweite Menge W2. Jeder Achsenton kann eine der beiden Rollen einnehmen, die nicht an dieser Achse gespiegelt werden: auf s2 kann also a2 oder d2 liegen, nicht aber b2 oder c2. Dies ergibt zwei weitere Viererzyklen V2a und V2b.

Es bleiben vier Töne übrig, für die es (da ja v2, s2, v3 und w3 in den Mengen V2 und W3 bleiben FIXME STIMMT DAS ??) keine weiteren Einschränkungen, also eine Vierermenge W3 und vier verschiedene Zyklen V3a bis V3d.

XXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXX

Die Töne a1 und d1 sind mit ihren Spiegelbildern an der Achse s4 in V1 enthalten.

Falls ihre Spiegelbilder an der Achse s2 (a1.s2=v2 und d1.s2=w2) in einem anderen Viererzyklus != V1 enthalten sind, dann zusammen mit ihren Spiegelbildern an s4 (denn die an s2 würde ja verbotenerweise einen Ton aus V1 wiederholen.) Also liegen sie dann ebenfalls in den Mengen (/auf den Zykluspositionen) a oder d.

für die sie enthaltenden Vierermengen gilt
v2 in Wv = { v2, v2.s4, v2.s1, v2,s1.s2 }
w2 in Ww = { w2, w2.s4, w2.s1, w2,s1.s2 }

1. Das ist gleichbedeutend damit, dass b2 und c2 (die lt. Konstruktionsprinzip ja an s2 auf einander gespiegelt werden) nicht auf v2 und w2 fallen dürfen. Genau das sagen vier der sechs Ungleichungen:
   a2 != c1 <==> a2.s1.s2 != c1.s1.s2 <==> c2 != d1.s2=w2 [neq02]
   a2 != (a1.s1.s2.s1).s2.s1 = d1.s2.s1 <==> a2.s1=b2 != d1.s2=w2 [neq23]
   a2 != a1.s2.s1 <==> a2.s1=b2 != a1.s2=v2 [neq20]
   a2 != b1 <==> a2.s1.s2 != b1.s1.s2 <==> c2 != a1.s2=v2 [neq01]
2. (
   NB: Für b1 und c1 und ihre Spiegelbilder gelten naturgemäßerweise dieselben Bedingungen, mit ausgetauschten Spiegelachsen. Diese Bedingungen fügen aber nichts neues hinzu, da sie bereits im Ungleichungssystem enthalten sind:
   c1.s4 != d2 = a2.s4 <==> c1 != a2 [neq2]
   c1.s4 != a2 <==> d1 != a2 [neq3]
   b1.s4 != a2 <==> a1.s1.s1.s2.s1 != a2 <==> a1.s2.s1 != a2 [neq20]
   c1.s4 != a2 <==> a1.s1.s2.s1.s2.s1 != a2 [neq23]
   )

Der erste Viererzyklus wurde definiert zu
V1 = < a1, b1=a1.s1, c1=a1.s1.s2, d1=a1.s1.s2.s1 >

Sei der Winkel von s1 zu s2 gleich "alpha", dann ist x.s1.s2 eine Rotation um den Winkel 2*alpha.
[defAlpha] s2-s1=alpha
[defT] T = 2*alpha

Schreiben wir also kurz
x.T = x.s1.s2 und x.2T = x.(s1.s2).(s1.s2), etc.
und damit
V1 = < a1, a1.s1, a1.T, a1.T.s1 >
wie in der rechten Hälfte von voranstehender Abbildung.

Allgemein: jeder Ton x bestimmt eine Vierermenge
W(x) = {x, x.s1, x.T, x.T.s1 }
Diese kann auf verschiedene Weise zum Viererzyklus angeordnet werden. Jeder solcher hat die Gestalt wie V1, also
< y, y.s1, y.T, y.T.s1 > mit y in W(x)

Bauen wir die nächsten Viererzyklen V2 und V3 um die kritischen Töne v2 und w2.

Zunächst gilt
[neqV2W2] v2 != v2 <==> a1.s2 != a1.s4.s2 <==> a1 != a1.s4 = d4 (laut [alleDisj])

Falls v2.s4=w2, dann liegen sie in derselben Vierermenge: Ww = { w2, w2.s4, w2.s1, w2,s1.s2 } = {v2.s4, v2.s4.s4, v2.s4.s1, v2.s4.s1.s2 } = {v2.s4, v2, v2.s1.s2, v2.s1 } = Wv
liegen v2 und w2 in zwei Viererzyklen V2a und V2b, die aus denselben vier Tönen bestehen, diese aber anders den Mengen a bis d zuordnen.
Ist hingegen v2.s4!=w2, dann gibt es vier verschiedene derartige Zyklen.
Es gilt:
v2.s4 = w2 <==> a1.s2.s4 = a1.s4.s2 <=> a1.s2.s1.s2.s1 = a1.s1.s2.s1.s2 <==> a1.s1.s2.s1.s2.s2.s1.s2.s1 = a1 <==> a1.4T = a1 <==> alpha = 1.5

FIXME WEITERMACHEN

Wir können also den nächsten Viererzyklus auf zwei Weisen bestimmen:
V2a = {a2a=a1.s2=v2, b2a=a2a.s1=a1.s2.s1, c2a=a2a.s1.s2=a1.s2.s1.s2, d2a=a2a.s1.s2.s1=a1.s2.s1.s2.s1}
= {a1.s1.T, a1.s1.T.s1, a1.s1.2T, a1.s1.2T.s1 }
und
V2b = {a2b=a1.s4.s2=a1.s1.s2.s1.s2=w2, b2b=a2b.s1=a1.s1.s2.s1.s2.s1 c2b=a2b.s1.s2=a1.s1.s2.s1.s2.s1.s2 d2b=a2b.s1.s1.s1=a1.s1.s2.s1.s2.s1.s2.s1}
= { a1.2T, a1.2T.s1, a1.3T, a1.3T.s1}

Der letzte Viererzyklus ergibt sich ebenso, indem a2.s2 oder a2.s4.s2=d2.s2=a2.2T als Ausgangspunkt gewählt wird. Dies gibt die Lösungen
V3aa = {a1.s1.T.s2, a1.s1.T.s2.s1, a1.s1.T.s2.T, a1.s1.T.s2.T.s1}
V3ab = {a1.s1.3T, a1.s1.3T.s1, a1.s1.4T, a1.s1.4T.s1 }
V3ba = {a1.2T.s2, a1.2T.s2.s1 a1.2T.s2.T, a1.2T.s2.T.s1 }
V3bb = {a1.4T, a1.4T.s1, a1.5T, a1.5T.s1 }

(V1,V2a,V3aa), (V1,V2a,V3ab), (V1,V2b,V3ba), (V1,V2b,V3bb) sind also theoretisch vier vollständige Zerlegungen, für jeden möglichen Winkel alpha.
Diese reduzieren sich allerdings eventuell dadurch, dass bei einem bestimmten Wert von alpha bestimmte Spiegelungen/Rotationen mit bereits benutzten Tönen zusammenfallen.

Dies ist zu untersuchen für alpha = -2.5 bis alpha = 3.
FIXME WEITERMACHEN

Welche Möglichkeiten gibt es unter diesen Bedingungen? Folgende Ausgangsvoraussetzungen lassen sich o.b.d.A. festsetzen:

1. Bezeichnen wir im folgenden wie üblich die Tonklassen mit den Zahlen 0 bis 11, geschrieben als "t0" bis "t11". Für Notenbeispiele, die dem Musiker wohl anschaulicher sind, setzen wir zusätzlich "to=c" bis "t11=h".
2. Messen wir Winkel im Bogenmaß bezgl. des Kreisumfanges von 12 Halbtonschritten.
3. Ein Spiegelungsergebnis kann nun auch durch Rotation ermittelt werden: sei gamma der Winkel eines Tones zu einem gegebenen Nullpunkt, und alpha der der Spiegelachse, dann ist die Position des Spiegelbildes
   alpha - (gamma-alpha) = 2*alpha - gamma
4. Jeder Winkel alpha zwischen s1 und einer anderen Achse bestimmt die Lage aller drei Spiegelachsen.
5. Setzen wir die Achse s1 zwischen t11 und t0.
6. Es gilt 0.5 <= alpha <=3, wobei der Fall alpha=3, ein Sonderfall ist, denn dort gilt s2=s4.
7. Jeder Ton ist durch Spiegelung an s1 auf einen anderen abgebildet, und zwar die Menge a auf b und Menge c auf d. Dies zeigen die horizontalen Linien in folgender Graphik.
8. Wir suchen ja die strukturell verschiedenen möglichen Zerlegungen des zwölf Tonklassen. Bei einer jeden solchen Zerlegung gilt für jeden Ton eine zweite Spiegelachse s2 oder s4.
9. Die Mengen b und c werden an s2 aufeinander gespiegelt.
   Die Mengen a und d werden an s4 aufeinander gespiegelt.
10. Setzen wir t11=h als a1, den ersten Ton aus a, und t0=c als b1, den ersten Ton aus b.
11. sN sei die zu b1 nähere Achse, sF die fernere.

All das zeigt folgende Graphik.

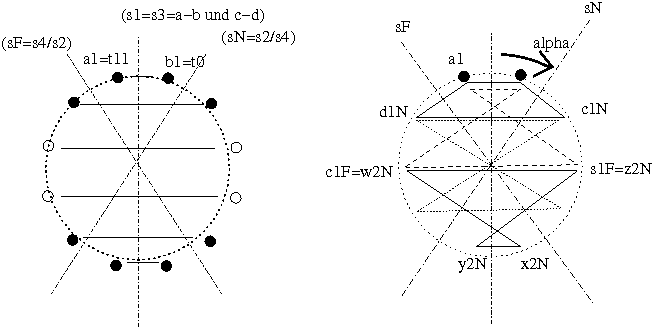
Ab hier gibt es zwei Möglichkeiten: zur Achse s2, die b1 auf c1 abbildet, kann sN oder sF gewählt werden.
Es ergeben sich zwei verschiedene erste Spiegelungsspuren V1N und V1F:
V1N = { a1, b1=a1.s1, c1N=a1.s1.sN=2*alpha-b1, d1N=a1.s1.sN.s1=a1.sF=(-2*alpha)-a1}
V1F = { a1, b1=a1.s1, c1F=a1.s1.sF=(-2*alpha)-b1, d1F=a1.s1.sF.s1=a1.sN=2*alpha-a1}
(Diese sind mit durchgezogenen und gestrichelten Linien in obigem Diagramm eingetragen.)

Die einmal getroffene Zuordnung von sN und sF zu s2 und s4 muss beibehalten werden:

Gesetzt, s2=sN sei gewählt. c1F=b1.sF ist dann nicht in V1N. (Es ist verschieden von a1, weil sF!=s0; von b1 weil sF nicht durch b1 geht FIXME EINFÜHREN, von d1N=a1.sF, weil a1!=b1; von c1N, weil sN!=sF).
Also muss c1F einer anderen Spur angehören. Heiße diese V2N. c1F heiße wegen dieser Rolle auch w2N.
Dann kann w2N.sF=c1F.sF=b1 nicht in V2N sein, da es schon in V1N ist. w2N muss also an der anderen Achse sN gespiegelt werden, und es ergibt sich
V2N = {w2N, x2N=w2N.sN, y2N=w2N.sN.s1, z2N=w2N.sN.s1.sF=w2N.s1}

Die Buchstabenwahl "w,x,y,z" für die Töne des zweiten Zyklus bedeutet, dass die Zuordnung zu den zu konstruierenden Mengen "a,b,c,d" nicht feststeht:

w2N wird (abgesehen von s1) an sN gespiegelt, also an derselben Achse wie b1 und c1N. Deswegen kann w2N zur Menge b oder zur Menge c genommen werden. Dasselbe gilt für x2N. Hingegen sind y2N und z2N durch sF verbunden, wie a1 und d1N, können also zur Menge a oder d genommen werden. Es ergeben sich also (für den Fall s2=sN) bis hierhin zwei Möglichkeiten:
a = {a1,x2N} b={b1,y2N} c={c1N,z2N} d={d1N, w2N}
oder
a = {a1,y2N} b={b1,x2N} c={c1N,w2N} d={d1N, z2N}
Dies entspricht den beiden Durchlaufmöglichkeiten der zyklischen Folge w,x,y,z,w,x,y,...

Dasselbe gilt nun wenn man x2N betrachtet: Sein Spiegelbild an sN ist in V2N enthalten, das an sF muss also im dritten Zyklus V3N enthalten sein. Auch dessen Töne sind damit eindeutig determiniert und können auf zwei Weisen auf die Mengen a,b,c,d verteilt werden.

All das gilt auch wenn zu Beginn s2=sF gesetzt wird (gestrichelte Liniein im Diagramm).

Es gibt also die initiale Entscheidung zwischen sF und sN, und dann in V2 und V3 die je zwei Zuordnungen der Töne zu den Mengen, macht insgesamt 8 strukturell unterschiedliche Mengenaufteilungen, also solche, die nicht durch Transposition oder Spiegelung in einander überführt werden können. (FIXME WARUM??? WINKEL???)

Dies gilt für die Winkel alpha=1 und alpha=2.

Für die Situationen alpha=0.5, 1.5 und 2.5 mit den "materiellen" Spiegelachsen s2 und s4 gilt die Einschränkung, dass in derjenigen Ableitungsstufe Vn, in welcher ein Ton auf einer Spiegelachse liegt, nur die jeweils andere für diesen Ton benutzt werden kann. Es herrscht also keine freie Wahl zwischen sN und sF und die Gesamtzahl der Möglichkeiten reduziert sich auf vier je Winkel.

Ein weiterer Sonderfall ist alpha=3. Dort gilt s2=s4, also eine Wahl zwischen den Achsen kann garnicht stattfinden. Dafür können aber in V2 und V3 die vier Töne auf vier verschiedene Weise (qua Rotation) den Mengen a bis d zugeordnet werden, was sechzehn Möglichkeiten ergibt.

Zusammengefasst:

FIXME WEITERMACHEN / stimmt das? Spiegelungsdoubletten/Symmetrieen ??

Damit lassen sich alle Möglichkeiten der dodekaphonen All-Modi-Reihen relativ einfach aufzählen:
Setzen wir die vier Spiegelachsen im Abstand von drei(3) Tonstufen, wie als notwendig nachgewiesen. Setzen wir einen beliebigen Ton "A2" als Mittelpunkt eines Dreiersegmentes und fordern o.b.d.A, dass dieser der Menge "a" angehöre.
Folgen wird seinen Spiegelbilder in einer bestimmten Richtung, durchschreitend die oben definierten Mengen b, c, d, so gibt es zwei Möglichkeiten: FIXME STIMMT NICHT FUER SYMMETRISCHE TONMENGEN entweder ist das erste in der Menge R, danach folgt dann I, dann IR. Oder aber die nächste Menge ist IR, dann I, dann R:

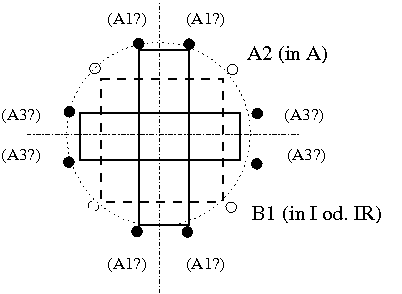
Diese Entscheidung wird aber erst in einem späteren Schritt relevant, wenn die Ton-Mengen zu Ton-Folgen angeordnet werden. Hier fragen wir zunächst nach den grundsätzlich verschiedenen Möglichkeiten der "Formen der Mengen", modulo Transposition und Umbenennung "A/I/R/IR". (Wir unterscheiden also nicht verschieden Verwendungen derselben Reihe, wo verschiedene Teilreihen als "A" oder "I" benannt werden, sondern nur strukturelle Unterschiede jenseits der Benennung/Verwendung.) Setzen wir dazu in Fall "0" die beiden Nachbartöne aus demselben Dreiersegment auch in die Menge "a" und lassen in den folgenden Fällen diese beiden Töne durch Spiegelung an den Achsen sich entfernen. Jeder der Nachbarn hat also insgesamt vier Positionen, Dieses "Sich-Entfernen" entspricht einer Bewegung über die Kanten der Rechtecke in vorangehender Graphik, resp. auf den Klammern und Bögen oben in der folgenden. In Noten umgesetzt bedeutet dies, dass der sich ändernde Ton immer abwechselnd einen Halbtonschritt vollzieht, und danach eine Quarte, je nachdem ob er einen Vierteltonschritt oder eine große Sekunde plus Vierteltonschritt von der Spiegelachse entfernt ist. (Nennen wir dies Austausch-Schritt.)

Die möglichen Austausch-Schritte ergben zunächst eine Gesamtzahl von 16 Formen für eine Dreiermenge. Aber bei alle unsymmetrischen Kombinationen darf deren Spiegelbild nicht mitgezählt werden, da dieses sich ja als Form der gespiegelten Nachbarmengen ("b" und "d") ergibt, also "modulo Umbenennung" nichts neues beiträgt.

Die Anzahl der symmetrischen Formen einer einzelnen Dreiermenge ist vier(4), FIXME FUNF 0 4 6 7 9 also gibt es insgesamt
4 + ((16-4)/2) = 4 + 6 = 10 wesentlich verschiedene Möglichkeiten zur Aufteilung der Gesamtreihe.

Folgende Auflistung zeigt nur die, wo der Abstand des rechten Nachbarn größer-oder-gleich (>=) dem des linken ist. Dabei messen wir nicht modulo, sondern lassen die Nachbarn auf ihren Start-Seiten. Im Gegensatz dazu sind die Darstellungen mit graphisch ausgefüllten Leerstellen die zyklischen Umsortierungen mit dem kürzesten Gesamtumfang:

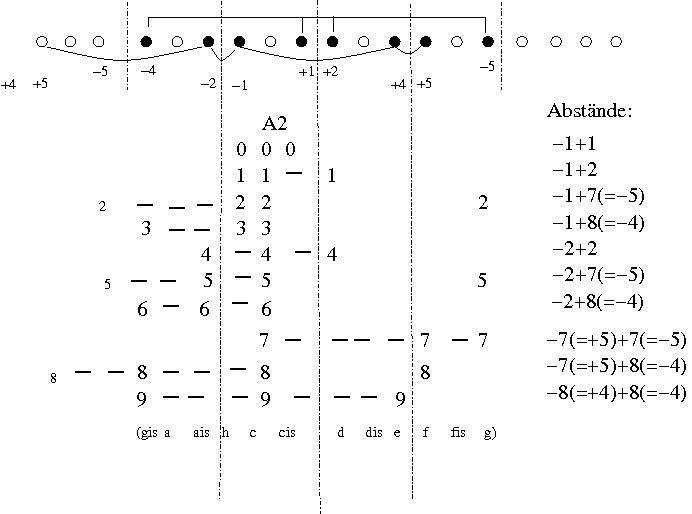
Notabene sind Fälle 4 und 6 verschieden. Die Tonabstände sind zwar identisch, aber nicht die Lage der Mengen zu den Spiegelachsen: in 6 bilden Menge a = Modus A und die an der linken Achse gespiegelte Menge d (Modus IR oder I) eine zusammenhängende Klein-Sekund-Menge, getrennt von den anderen beiden Modi; in 4 sind alle vier Modi mit einander verschränkt. Dies bewirkt in in der musikalischen Wirkung einen schwerwiegenden Unterschied!
Generell gilt: Erstreckt sich eine Menge über zwei benachbarte Dreier-Segmente, so (a) füllt sie mit einer ihrer Spiegelungen eine Halb-Oktave lückenlos aus und (b) hat ganz im Gegenteil mit ihrer anderen Spiegelung keine Überlappung. (Für diese andere und die noch fehlende vierte gilt natürlich dasselbe, entsprechend!-)

Dies gilt für Fälle 1, 3 und 6.

^{^Inh} 3.2 Konstruktion von Reihenabläufen

FIXME stimmt nicht, auch (ii) verschieden für symmetrische und unsymmetrische Mengen!

Um aus einer gegebenen Zerlegung nach einer der Mengenformen 0 bis 9 nun eine All-Modi-Reihe zu machen, muss festgelegt werden (i) die Reihenfolge der Töne aus der Menge a innerhalb von Modus A, (ii) ob in Menge b (jenseits der "rechten Spiegelachse" eineinhalb Tonschritte oberhalb von A1) der Modus I oder IR liegen soll, und (iii) in welcher Reihenfolge die Modi der Teilreihen die Reihe bilden.

Zu (i):
Bei drei nicht-symmetrisch angeordneten Tonhöhen gibt es 3!=6 Anordnungsmöglichkeiten. Alle diese sind voll-modal, also für unsere Zwecke möglich.
Bei den symmetrischen Abständen (Zerlegungen 0, 4, 6 und 9) sind die linearen Abfolgen ungeeignet, da IR-symmetrisch, bleiben also nur 4. Insgesamt gibt es also
6*6 + 4*4 = 36 + 16 = 52
verschiedene Kombinationen von Mengenzerlegungen und erster Teilreihe.

Zu (ii):
Die doppelt-gespiegelte Tonmenge (c) ist wieder deckungsgleich mit der Ausgangsmenge (a), kann also nur den Modus "R" repräsentieren
FIXME gilt nur bei unsymmetrischen !!?!
Die einfach gespiegelten müssen sich also in I und IR teilen, -- es gibt also zwei Möglichkeiten, zu welchen Modi die benachbarten, einfach gespiegelten Tonmengen (b und d) angeordnet werden sollen.

Zu (iii):
Zuletzt kann, angenommen die Menge a, Modus A, stehe als erster, die Reihe in 3!=6 Weisen durch Aneinanderreihung der anderen Modi komplettiert werden. Dabei bestimmt der letzte Modus die Symmetrie der Gesamtreihe, wie oben nachgewiesen, und der dritte die der Halb-Reihen, siehe oben Tabelle [T4symm], Abschnitt 2.5.
Wir wählen die Benennung so, dass sie diese Symmetrien in dieser Reihenfolge wiedergibt, welche der abnehmenden Wichtigkeit entspricht. Die IR-R-Anordnung ist also ausgeschrieben gleich A-R-I-IR: die Reihe ist als ganze IR-symmetrisch und die Hälften je R-symmetrisch.

^{^Inh} 3.3 Beispiele in Noten für alle Zerlegungsformen

Die folgenden Notenzeilen enthalten synthetische, ansonsten völlig beliebige Beispiele für All-Modi-Reihen konstruiert nach den obenstehenden Mengenzerlegungsformen. Sie dienen nur dazu, den eher musikalisch als mathematisch vorgebildeten Lesern eine Intution von den bisherigen Ergebnissen zu verschaffen.
Als "erster gesetzter Ton A2" in obenstehender Konstruktion ist immer die Tonklasse "c" gewählt; die Reihenfolge der Teilreihen entspricht den Mengen a, b, c, d ohne weitere Umordnung, die noch zusätzlich jedesmal möglich wäre.

Einige Anmerkungen:
Alle Beispiele für symmetrischen Mengezerlegungsformen nutzen aus, dass nur dort auch Menge b das "R" realisieren kann. (Bei den unsymmetrischen kann "R" ja nur als Menge c, "Drehung" von a, als Transposition in sechs Halbtonschritten auftreten, wie oben ausführlich hergeleitet.)
Die meisten Beispiele für die unsymmetrischen zeigen, dass dann auch die lineare "ungeknickte" Abfolge der Tonhöhen voll-modal ist, wenn auch meist nicht mit großer Signifikanz.
(Der Verfassers frühe f-moll-Sonate beruht auf Intervallen entsprechend Beispiel 2.)

Gemäß dem gewählten Aufzählungs-/Konstruktion-Prinzip gehen die meisten Zeilen aus der darüberstehenden durch Austausch nur einer Tonklasse je Teilreihe hervor; dies zeigt schön den oben definierten "Austausch-Schritt", der immer in einem Halbtonschritt oder einer Quarte besteht, siehe die langen und kurzen Kanten der Rechtecke in oben stehender Graphik.

Beispiel 1 zeigt die säuberliche Trennung der Tonbereiche der Hälften a U b und c U d, was rezeptionstechnisch durchaus wirkmächtig werden kann.
AEHNLICH FIXME ...
In Zeilen FIXME 4 zeigt sich die Herkunft des Fünf-Linien-Notationssystems aus der Diatonik: mit "ais" und "dis" notiert wie die anderen Beispiele erscheinen die gleichen Intervallverhältnisse der beiden Reihenhälfte viel weniger klar.
Man erkennt auch deutlich den Unterschied zwischen 4 und 6, wie oben erwähnt: dort alle Teilreihen mit beiden Nachbarn sich im Tonraum überschneidend, hier Trennung und kompakter Zusammenhalt der Mengen b U c und a U d,

Mit M-7 haben zum ersten Mal beide Nachbartöne sich weiter als die halbe Oktave entfernt. Die normierung auf kleinstes Außenintervall liefert ungelichmäßige Intervalle nach Zeile "7", die auch einfach monoton angeordnet noch voll-modal sind. Zeile "7b" zeigt die wahre Symmetrie, die also nur in "Hakenform" voll-modal ist (diese Oktavlagen monoton angeordnet wären IR-Symmetrisch!)

M-8 zeigt lustigerweise tonale Dreiklänge.

M-9 hat das Alleinstellungsmerkmal dass es aufgefasst als Tonklassen niemals voll-modal ist, da es eine total gleichmäßige Teilung der Oktave bedeutet. Die übrigen symmetrischen Mengen konnten immer auf ein "kleinstmögliches Außenintervall" normiert werden, und darin dann eine "Hakenform" definiert werden, also eine andere Reihenfolge als eine der beiden monotonen FIXME EINFÜHREN Anordnungen. Dies hist hier nicht möglich.
Wir haben deshalb im Notenbeispiel oben darauf verzichtet, eine solche anzudeuten, denn dies würde implizit eine Pardigmenwechsel verlangen: den Übergang von Tonhklassen zu oktav-versehenen Tonhöhen.

^{^Inh} 4 Minimale voll-modale musikalische Ausgangsgebilde, Haken

^{^Inh} 4.1 Konstruktion eines minimalen voll-modalen Materials

Wenden wir uns nun dem zweiten grundlegenden Teilthema dieser Untersuchung zu und fragen nach den minimalen voll-modalen musikalischen Gebilden.

Dabei wird sich unten (Widerlegung von V4-b) als wichtig herausstellen, dass es um Abfolgen von Ereignissen in der Zeit geht, wobei ein Ereignis nicht mehr nur, wie oben definiert, eine Wert in einer abstrakten Liste von Werten ist, sondern eine mit Sinnen wahrgenommene Informationseinheit, die eine bestimmte Zeit dauert und dabei eindeutig von den Nachbar-Ereignisses unterscheidbar ist.

Beginnen wir nun mit den einfachsten derartigen Konstellationen und überprüfen diese auf die Darstellbarkeit der vier Modi, was nach voranstehenden Ausführungen ja gleichbedeutend ist mit der Abwesenheit der entsprechenden störenden Symmetrie.

V1 Erster Versuch: Ein einziges Ereignis. Dieses kann nur einen einzigen Wert darstellen. Alle Operation führen folglich zum selben Ergebnis, kein Modus ist unterscheidbar, es gilt
A=I=R=IR.

V2 Zweiter Versuch: Zwei Ereignisse, die denselben Wert darstellen. Dies bedeutet keine Verbesserung: die I-Operation ist bei nur einem Wert zwangsläufig die Identität, und die R-Operation bei zwei verwechselbaren Ereignissen ebenfalls.

V3 Dritter Versuch: Zwei Ereignisse, die zwei verschiedene Werte darstellen. Hierbei bringt die R-Operation einen eindeutigen Unterschied, der im Austausch der beiden Werte bzgl. der Reihenfolge ihres Auftretens besteht. Dasselbe Ergebnis liefert aber auch die I-Operation. Die IR-Operation folglich wieder das Original. Wir haben eine Punktsymmetrie bezgl. eines immateriellen Zentrums zwischen beiden Ereignissen und beiden Werten vorliegen. Auch diese Konstellation ist also nicht hinreichend:
A=IR != I=R.

V4 Vierter Versuch: Drei Ereignisse, die zwei verschiedene Werte darstellen. Es gibt zwei Unterfälle:

V4-a Symmetrische Anordnung der Werte bezgl. der zweiten Position: a-b-a. In diesem Falle hat die Positions-Spiegelung R kein merkliches Resultat. Allerdings die I-Operation, die in b-a-b resultiert. Also gilt
A=R!=I=IR.

V4-b Unsymmetrische Anordnung der Werte: a-a-b. In diesem Falle sind tatsächlich alle Modi unterscheidbar: A=aab, I=bba, R=baa und IR = abb. Allerdings ist die Voraussetzung, dass die mit demselben Wert an einander grenzenden Ereignisse auf "irgendwie andere Weise" als Ereignisse überhaupt kenntlich werden! Das ist selbstverständlich im klassischen Anwendungsfall unmittelbar gegeben, wenn man z.B. diese drei Ereignisse als drei Anschläge auf dem Klavier realisiert, mit den entsprechenden Tonhöhen.
Allerdings setzt das die Existenz weiterer, paralleler Parameterschichten voraus, hier die Hüllkurve des Anschlages, o.ä., die diese drei Ereignisse überhaupt als solche konstituiert. Hat man ausschließlich den einen, hier untersuchten Wertebereich zur Verfügung, ist "a--a" von "a" nicht unterscheidbar. Anders formuliert: nur ein Wechsel eines Parameter-Wertes konstituiert überhaupt ein "Ereignis" im Sinne von Wahrnehmung und/oder Gestaltung.

Also ist dieser Fall auch noch nicht hinreichend, wenn man im Sinne der Forderung nach Minimalität eine solche notwendige zweite Parameterschicht ablehnt.

V5 Fünfter Versuch: Drei Ereignisse, die drei verschiedene Werte darstellen.
Nennen wir die Werte "O", "M" und "U", für "oben", "mitte" und "unten". Die R-Operation bildet das zweite Ereignis auf sich selbst ab, die I-Operation den Wert M auf sich selbst. Wenn also der Wert M auf das zweite Ereignis fällt, dann wird dieses von keiner einzigen Operation verändert, trägt also zur entstehenden Gestalt nichts bei. Wir haben dann dieselbe Situation wie in V3, welche ja nicht hinreichend unsymmetrisch ist. (Nur ist die dort "virtuelle" Symmetrie-Achse hier durch eine "materielle" ersetzt.)

^{^Inh} 4.2 Doppelhaken

Da die vier Grundhaken die minimalen voll-modalen Materialien sind, eignen sie sich vorzüglich als Teilreihen/Ausgangsmaterial von All-Modi-Reihen. In den folgenden beiden Abschnitten übertragen wir die oben abstrakt gewonnenen Erkenntnisse auf dieses konkrete Material. Wir beginnen wie oben wieder "bottom-up", also zunächst mit Modi-Paaren. Deren konkrete Version heiße "Doppelhaken".

Es gilt wie oben:
Jede Folge A;R ist R-symmetrisch.
Jede Folge A;IR ist IR-symmetrisch
Jede Folge A;I ist nicht symmetrisch.

Dies sind alle möglichen Folgen, und jedes dieser Modi-Paare kann auf einen der vier Haken als sein Ausgangsmaterial A angewandt werden, wodurch sich drei Mengen von je vier Doppelhaken ergeben. Dieselbe Gesamtzahl ergibt sich als die Anzahl aller Zweier-Sequenzen aus vier Elementen "vier über zwei".

Die drei Mengen werden nach ihrem Bildungsprinzip benannt, also I-, R- und IR-Menge. Sie unterscheiden sich nicht nur in den Symmetrieeigenschaften, sondern bestimmen auch die meisten anderen Eigenschaften. Zwei Haken können sich lt. [hakenProp] in MPos und VArt unterscheiden. In jedem Doppelhaken aus ...
... der R-Menge ist in beiden Haken MPos verschieden, VArt aber gleich.
... der I-Menge ist in beiden Haken MPos gleich, VArt aber verschieden.
... der IR-Menge sind in beiden Haken MPos und VArt verschieden.

Darüber hinaus wird besonders wichtig für die konkrete kompositorische Umsetzung das Anschluss-Intervall zwischen den beiden Haken.

Bei jeder Folge A;R stoßen gleiche Buchstaben aneinander, das Anschlussintervall hat also immer die Größe null(0), unabhängig von der Wahl des Ausgangsmaterials.
Auf diese Doppelhaken kann I und IR angewandt werden, welche beide dasselbe, vom Ausgangsmaterial verschiedene Resultat hervorbringen. Die Operation R hat keinen merklichen Effekt.

Bei jeder Folge A;I stößt der letzte Wert des ersten Hakens an seinen invertierten ersten Wert. Von erstem und letztem Wert ist immer genau einer gleich M. Wenn man beliebig einen dieser Werte invertiert, bleibt das so. Also ist genau einer der beiden aneinanderstoßenden Werte gleich M und die Größe des Anschlussintervalles immer gleich eins(1).
Auf diese Doppelhaken können (mit merklichem Effekt) alle Operationen I, R und IR angewandt werden, sie weisen keine Symmetrie auf.

Bei jeder Folge A;IR stößt der letzte Wert "x" des ersten Hakens an seine eigene Invertierung. Ist "x=M", so ist der Anschluss ebenfalls null, ansonsten aber zwei(2).
Auf diese Doppelhaken kann I und R angewandt werden, welche beide dasselbe vom Ausgangsmaterial verschiedene Resultat hervorbringen. Die Operation IR hat keinen merklichen Effekt.

Bei den Doppelhaken vom Typ A;R (A;IR) haben ja jeweils nur die Operationen I und IR (I und R) einen merkbaren Effekt. Es werden also nur zwei der vier Haken untereinander durch genau diese Operation verbunden. Das liegt daran, dass in beiden Haken dieser Hakenpaare das "M" an je anderer Stelle steht: ein Rückwärtslesen kann im Ergebnis keine andere Reihenfolge liefern: steht das M im letzten Haken an letzter Stelle, so steht es sowohl im ersten Haken an erster Stelle, beim Vorwärtslesen, als auch im Ergebnis des Rückwärtslesens, et vice versa.
(Die I-Operation kann ohnehin die Position des M nicht verändern.)

Also vermittelt zwischen den je zwei Untermengen, die sich durch die Position des M unterscheiden, immer nur die zusätzliche Operation P(_;_), die die beiden Haken des Doppelhakens explizit vertauscht. In folgender Tabelle entspricht sie einem Wechsel zwischen Zeile 1 und 2 (4 und 5).

Bei den Doppelhakens vom Typ A;I ist das nicht nötig: die I-Operation vertauscht ja genau die Doppelhaken, indem sie die Vokale austauscht; die R-Operation verändert die Position des M. Dadurch sind alle vier Haken dieses Typs durch die vier Operationen aus einander erzeugbar.

Folgende Tabelle fasst diese Zusammenhänge zusammen. Dabei ist die Auswahl des Hakens "OM" als Ausgangsmaterial völlig beliebig und für die Darstellung irrelevant, da (a) durch die Operationen ja ohnehin alle zwölf(12) möglichen Doppelhaken erzeugt werden, und (b) nur die strukturellen Eigenschaften der Doppelhaken ("MPos" und "VArt" wie oben definiert) für ihre internen Eigenschaften und gegenseitigen Beziehungen maßgeblich sind. (Die Buchstaben a,r,i,ir in der ersten Spalte und A,R,I,IR in der Kopfzeile meinen dieselben dodekaphonen Operationen, aber die Kleinbuchstaben sind bezogen auf das Binnenverhältnis der beiden Haken im Doppelhaken, die großen auf die Operationen auf den Doppelhaken als ganzen!)

MPos VArt A I R IR P(_;_) card(G) AnschlInt 1 a;r diff equ OMMO W UMMU M =A =I MOOM 2 0 2 r;a diff equ MOOM A MUUM V =A =I OMMO 2 0 3 a;i equ diff OMUM W+ UMOM M+ MUMO +W MOMU +M =I 4 1 4 a;ir diff diff OMMU N- UMMO N =I =A MUOM 2 0 5 ir;a diff diff MUOM e- MOUM e =I =A OMMU 2 2

Abbildung 6: Doppelhaken und ihre Modi

Wir bezeichen die Doppelhaken auch mit den Buchstaben, an deren Form ihre Kontur erinnert:
W, M, A, V sind offensichtlich.
+W bedeutet "W mit einem zusätzlichen Anstrich davor", W+,+M,M+ entsprechend.
N steht für sich, und "e" für das "kleine e der Deutschen Kurrentschrift", und N- und e- für deren Spiegelung an beliebiger (sic!, vertikaler oder horizontaler) Achse.

Dabei erweist es sich als mnemotechnisch nützlich, dass A, V, W, M intern symmetrisch sind und (zusamen mit N) das interne Anschlussintervall=0 haben; alle mit "+" haben einen Konturpunkt mehr, unter Aufgabe der internen Überlappung, haben also das Anschlussintervall=1; die "e"-Formen als die einzigen mit Kleinbuchstaben haben als einzige das interne Anschlussintervall=2.

^{^Inh} 4.3 Hakenreihen

Die konkreten Entsprechungen der All-Modi-Reihen angewandt auf die Grundhaken sind Hakenreihen, also Reihen, in denen alle vier Hakenformen MO, MU, OM und UM genau einmal auftreten. Es gibt sechs All-Modi-Reihen für die abstrakten Modi A, I, R und RI, nämlich die (wiederholungsfreien) Permutationen. Wird dies nun angewandt auf die Haken, ergeben sich vierundzwanzig Hakenreihen, da jeder der vier Haken als A gesetzt werden kann.

Während alle allgemeinen Erkenntnis bzgl. Symmetrie etc. selbstbverständlich auch in dieser konkreten Anwendung gelten, gibt es aber neue Eigenschaften, besonders bzgl. der sog. Anschlussintervalle, die erst mit der Anwendung auf das konkrete Material (=Haken) auftreten und die hier zu untersuchen sind.

Wir konstruieren die vierundzwanzig Reihen ausgehend von den Doppelhaken:
In voranstehender Tabelle gehen die jeweils übereinander stehenden Doppelhaken in den Zeilen 1 und 2 (4 und 5) durch die P-Operation aus einander hervor, die also nur die Haken gegeneinander austauscht.

Desweiteren gilt, dass die ersten beiden Modi der zu konstruierenden All-Modi-Reihen (die Haken des ersten Doppelhakens) wie oben ausgeführt (Vorüberlegung (a)) immer im selben Binnenverhältnis stehen müssen wie die letzten beiden. Auf jeden der vier Doppelhaken einer der drei o.e. Mengen kann also nur ein Haken derselben Menge folgen; die Einteilung in Mengen setzt sich also natürlich auf den Hakenreihen fort.

Zunächst in den Doppelzeilen 1 und 2 (4 und 5): Dort kann also auf jeden der eingezeichneten Doppelhaken nur ein weiterer aus eben derselben Doppelzeile folgen (nur diese haben dasselbe Binnenverhältnis), allerdings nicht der aus derselben Spalte (Verstoß gegen das Wiederholungsverbot der Einzelhaken).

In den Zeilen 1 und 2 (4 und 5) gibt es also acht Hakenreihen: ein beliebiger der vier Doppelhaken gefolgt von einem aus seiner Nachbarspalte. Diese beiden Doppelhaken stehen im Verhältnis A;I wenn sie aus derselben Zeile kommen, oder A:PI bei Zeilenwechsel.

Sei die zu konstruierende Hakenreihe zwecks Untersuchung der äußeren Symmetrie dargestellt als
(x;_;_;y).
x ist also der erste Haken des ersten Doppelhakens und y der zweite des zweiten; gemäß Abschnitt 2.5, Tabelle [T4symm] entscheidet ihr Verhältnis über die Symmetrie des Ganzen.

In der R-Menge (Zeilen 1 und 2) stehen die Haken der Doppelhaken intern im Verhältnis A:R. x und y müssen deshalb in einem der anderen Verhältnisse (I oder IR) stehen.
Wenn der zweite Doppelhaken ohne Zeilenwechsel ausgewählt wird, dann gilt
I(x;Rx) = Ry;y
weil die Doppelhaken intern das Verhältnis A;R realisieren und die Doppelhaken aus derselben Zeile das Verhältnis A:I. Damit aber auch
(I(x;Rx) = Ix;IRx = Ry;y ) ==> (IRx=y)
Zeilen 1 und 2 generieren also vier IR-symmetrische Reihen, nämlich alle Doppelhakenfolgen ohne Zeilenwechsel.

Bei Zeilenwechsel ist das Verhältnis
P(I(x;Rx)) = Ry;y
==> P(Ix;RIx) = Ry;y ==> RIx;Ix = Ry;y ==> Ix=y
und es liegt keine Symmetrie vor.

(Es herrscht aber immer R-Symmetrie für die Reihenhälften/Doppelhaken)

Die Doppelhaken in Zeile 1 haben je einen anderen Vokal an beiden Außenstellen, die aus Zeile 2 überall das "M". Für das zusätzliche Anschlussintervall i gilt:

In der IR-Menge (Zeilen 4 und 5) stehen die Haken der Doppelhaken im Verhältnis A:IR. x und y müssen deshalb in einem der anderen Verhältnisse (I oder R) stehen.
Wenn der zweite Doppelhaken ohne Zeilenwechsel ausgewählt wird, dann gilt (ähnlich wie gerade)
I(x;IRx) = IRy;y
Damit aber auch
(I(x;IRx) = Ix;IIRx = Ix;Rx = IRy;y) ==> (Rx=y)
Zeilen 1 und 2 generieren also vier R-symmetrische Reihen, nämlich alle Doppelhakenfolgen ohne Zeilenwechsel.

Bei Zeilenwechsel ist das Verhältnis
P(I(x;IRx)) = IRy;y
==> P(Ix;IIRx) = IRy;y ==> Rx;Ix = IRy;y ==> Ix=y
und es liegt keine Symmetrie vor.

(Es herrscht aber immer IR-Symmetrie für die Reihenhälften/Doppelhaken)

Die Doppelhaken in Zeile 4 haben beide je beide Vokale an den Außenstellen, genau entgegengesetzt. Die Doppelhaken aus Zeile 5 enden überall auf "M". Für das zusätzliche Anschlussintervall i gilt:

In der I-Menge (Zeile 3) stehen die Haken der Doppelhaken im Verhältnis A;I. Weil die Hakenreihe ja keine Wiederholung aufweisen darf, kann auf jeden der vier Doppelhaken sein R oder sein RI folgen. Nennen wir in Zeile 3 die Spalten "A" und "I" die AI-Hälfte und die Spalten "R" und "IR" die RIR-Hälfte. Dann kann auf jeden Doppelhaken aus der AI-Hälfte ein solcher aus der RIR-Hälfte folgen, oder umgekehrt. Die Doppelhaken in der AI-Hälfte beginnen mit einem Vokal und enden mit "M", in der RIR-Hälfte umgekehrt. Wenn also ein Doppelhaken aus der RIR-Hälfte beginnt, ist das neue Anschlussintervall i=2 oder i=0; wenn die AI-Hälfte beginnt, ist immer i=0.

Innerhalb der Doppelhaken/Reihenhälften herrscht keine Symmetrie. Wenn auf einen Doppelhaken (x;Ix) der Doppelhaken (Rx;RIx) folgt (das Charakteristikum sei der "geradzahlige Spaltenabstand"), dann herrscht nach Tabelle [T4symm] RI-Symmetrie für die Gesamtreihe. Wenn aber (RIx;Rx) folgt ("ungeradzahliger Spaltenabstand"), dann herrscht R-Symmetrie. Andere Fälle sind nicht möglich. Also sind alle Reihen mit Doppelhaken aus Zeile 3 (R- oder IR-) symmetrisch.

Folgende Tabelle fasst diese Ergebnisse zusammen und bezieht sich dabei auf voranstehende Tabelle. Unter "AnschlussInt" ist zunächst das neue, zwischen den Doppelhaken sich ergebende Intervall genannt, gefolgt in Klammern von den Werten innerhalb der Doppelhaken, übertragen aus voriger Tabelle.

^{^Inh} 4.4 Optimierung der Anschlussintervalle in Hakenreihen

Bei der Diskussion von klassischen melodischen Verläufen nennt man "totes Intervall" den tonhöhenmäßigen Abstand zwischen zwei aufeinanderfolgenden Ereignissen, der meist nicht als melodisches Intervall wahrgenommen wird, sei es, dass Pausen dazwischenliegen, sei es, dass das zweite Ereignis aus überzeugenden syntaktischen Gründen in einem anderen Kontext gehört wird als sein Vorgängerton (der folglich nur auf dem Papier überhaupt als solcher bezeichnet werden kann).

Metaphorisch gesprochen entstehen bei der Aneinanderfügung von zwei Haken zu Doppelhaken und von vier Haken zu Hakenreihen auch "tote Intervalle", nämlich beim Zusammenstroßen des letzten Wertes des einen Hakens mit dem ersten Wert des nachfolgenden Hakens, nämlich die Intervalle, die in der vorangehenden Stufe der Materialgewinnung noch garnicht auftraten und die jetzt hier, an dem Punkt des Materialaufbaus, an dem sie das erstemal entstehen, systematisch betrachtet werden sollen.

Für den Fall der Doppelhaken sind die Anschlussintervalle in obiger Tabelle aufgeführt.

Konstruieren wir nun (aus einer anderen Perspektive) Hakenreihen als Ganze, unter zwei entgegengesetzten Optimierungszielen: entweder möglichst kleine oder möglichst große Anschlussintervalle zu erzielen.

Das erste ermöglicht im Extremfall, wenn also das Anschlussintervall die Größe null(0) hat, also eine "Prime" geworden ist, sog. "Auslöschungen", d.h. Überlappungen von Motivabläufen: der Schlusston des einen dient gleichzeitig als Anfangston des zweiten. Eine übliche Satztechnik in klassischer Dodekaphonie und modernem Serialismus.

Möglichst große Anschlussintervalle hingegen unterstützen eine größtmögliche Deutlichkeit der Teilreihen als solche.

Zunächst gelten folgende Tatsachen über Haken und ihre möglichen Nachfolger:

1. Zwei(2) Haken enden auf M.
   Sie haben den Abstand eins(1) zu dem einen(1) anderen, der auch auf M endet, und den Abstand null(0) zu den beiden(2), die mit M beginnen.
2. Zwei Haken enden auf einen Extremwert X.
   Sie haben den Abstand null(0) zu dem einen(1) Haken, der mit X beginnt, den Abstand eins(1) zu dem einen Haken, der auch mit M beginnt und nicht mit X endet, und den Abstand zwei(2) zu dem Haken, der mit dem anderen Extremwert beginnt.

^{^Inh} 4.4.1 Maximierung der Anschlussintervalle

Betrachten wir zunächst die Forderung, dass alle Anschlussintervallen größer als der Einklang sein sollen, d.h. nicht verschmelzen dürfen, dass also nie ein Wert auf den gleichen Wert stoßen darf.

Um die Permutationen zu finden, die diesen Anforderungen genügen, beziehen wir uns auf die oben aufgestellten Beobachtungen in [hakenProp], dass nämlich

1. zwei(2) Haken mit M beginnen und enden,
2. aber nur je einer(1) mit O oder U.
3. und dass ein Haken der mit O oder U beginnt(endet), immer mit M endet(beginnt).

Die Ableitung einer Reihe ohne jede Auslöschungsmöglichkeit ist deshalb wie folgt:

1. Nehmen wir an, der zweite Haken ende auf M:

   ? ?

   ? M

   ? ?

   ? ?

2. Dann folgt daraus, dass der dritte mit O oder U beginnt, also auch mit M endet:

   ? ?

   ? M

   (o/u) M

   ? ?

3. Dann folgt aber daraus, dass auch der vierte mit O oder U beginnt, also auch mit M endet:

   ? ?

   ? M

   (o/u) M

   (o/u) M

   Das aber ist ein Widerspruch, da es nur zwei(2) Haken gibt, die mit M enden!
4. Also ende der zweite Haken z.B. mit O:

   ? ?

   ? O

   ? ?

   ? ?

5. Also beginnt der zweite Haken mit M:

   ? ?

   M O

   ? ?

   ? ?

6. Also endet der erste mit U, denn es gibt ja nur einen, der auf O endet, und der steht schon an Position zwei:

   ? U

   M O

   ? ?

   ? ?

7. Also beginnt auch der erste Haken mit M:

   M U

   M O

   ? ?

   ? ?

8. Also beginnt der dritte Haken mit U: denn mit O endet der davor, und Wiederholungen dürfen nicht auftreten, und die mit M beginnenden sind ja beide schon verbraten:

   M U

   M O

   U M

   ? ?

9. Und als vierter bleibt noch eine einzige Möglichkeit, die auch unsere Bedingung (keine Wiederholung als Anschlussintervall) erfüllt:

   M U

   M O

   U M

   O M

10. Selbstverständlich kann oben in Schritt vier auch U statt O gewählt werden. Dann erhalten wir durch die gleichen Schlüsse die einzige andere Lösung

    M O

    M U

    O M

    U M

Beide Lösungen bestehen aus zwei IR-symmetrischen Hakenreihen, nämlich "MUMO;UMOM = +W;M+" und "MOMU;OMUM = +M;W+"

Für beiden Lösungen gelten folgende Symmetrieeigenschaften:

1. die beiden Haken in allen vier Doppelhaken sind gegenseitig ihr I
2. die beiden Hälften jeder Hakenreihe sind gegenseitig ihr IR
3. deswegen ist jede Hakenreihe ihr eigenes IR
4. beide Lösungen sind gegenseitig ihr I (und deshalb auch ihr R)
5. beide Reihen gehen aus einander hervor durch die Permutation der Haken je Hälfte (denn I=P für die Doppelhaken der I-Menge)

Der "Hamming-Abstand", also die Summe aller Anschlussintervalle, ist bei beiden Lösungen 1+2+1. Unter der bisherigen Voraussetzung, das Intervall 0 zu verbieten, gibt es keine anderen Lösungen, ist vier(4) also die größtmögliche Intervallsumme.

Interessanterweise haben alle anderen Reihen der I-Menge bis auf diese beiden ein mittleres Anschlussintervall von null(0), also genau das Intervall, das hier ja weg-optimiert wurde!

Die Übergänge zwischen den Extremwerten U;O und O;U haben beide die Intervallgröße zwei(2) und können in der Tat auch beide zugleich in einer Haken-Reihen auftreten, nämlich durch die Kombination zweier Doppelhaken der IR-Menge:

Es gibt aber keine Reihe, die keinen Nullabstand enthält, in der diese beiden gleichzeitig vorkommen (denn die Reihen ohne Nullabstand haben wir ja gerade vollständig konstruiert, und da waren die nicht dabei !-)
Folglich gibt es derartige Reihen nur unter Inkaufnahme eines Null-Intervalles. Diese Reihen sind ...

Auch hier ist die maximale Intervallgröße also 4 (2+0+2).

Da zwei(2) die größtmögliche Intervallgröße ist, und diese nicht öfter als zweimal auftreten kann, und auch 1+2+1 von oben folglich nicht verbessert werden kann, sind diese vier Reihen damit auch sämtliche Lösungen mit maximal großen Anschlussintervallen.

Für die beiden neuen Lösungen gelten folgende Symmetrieeigenschaften:

1. alle vier Doppelhaken sind aus der IR-Menge
2. die beiden Doppelhaken je Hakenreihe sind gegenseitig ihr R und ihr I
3. deswegen ist jede Reihe ihr eigenes R
4. beide Reihen sind gegenseitig ihr I (und deshalb auch ihr IR)
5. beide Reihen gehen aus einander hervor durch die Permutation der Doppelhaken.

^{^Inh} 4.4.2 Minimierung der Anschlussintervalle

Das kleinste Anschlussintervall ist der "Einklang", das Intervall der Größe 0. Es kann nur auftreten wenn ein M oder derselbe Vokal an Ende des ersten und am Anfang des zweiten Hakens steht. Dafür gibt es vier resp. zwei Hakenkombinationen:

Sämtliche möglichen Abstände zwischen erstem und zweitem Haken sind ...

Die auf M enden haben den Abstand null(0) zu zwei(2) anderen und den Abstand eins(1) zu einem(1) anderen.

Die auf einen Extremwert enden haben die Abstände 0(null); 1(eins) und 2(zwei) zu jeweils einem anderen.

((
Anmerkung:
Wir reden hier allemal von Permutationen von Haken, mit "Wiederholungsverbot", so dass keiner "auf sich selbst" folgen kann. Wäre das aber erlaubt, so ergäbe sich in dabei für alle Hakenformen immer ein Anschlussintervall der Größe eins(1), denn eines der beiden Enden ist jeweils M, das andere dann ein Extremwert.
))

Die Konstruktion einer Permutation mit möglichst kleinen Anschlussintervallen erfolgt nun so:

1. Obige Tabelle zeigt, dass am besten das Intervall null(0) jedesmal ausgenutzt wird. Da drei der vier auftretenden Haken Nachfolger haben werden, hat entweder MO oder MU (oder beide) einen Nachfolger.
2. Setzen wir also, dass MO einen Nachfolger hat.
3. Wir testen zunächst was geschieht, wenn MO in der Kombination mit dem kleinsten Anschlussintervall, nämlich null(0), auftritt:

   ? ?

   ? ?

   M O

   O M

   ??

   ??

4. Wenn nun überhaupt etwas folgen soll, dann bietet nur MU die weiterhin minimale Summe der Anschlussintervalle:

   ? ?

   ? ?

   M O

   O M

   M U

   ??

5. Nun muß noch UM untergebracht werden. Wenn dieses an den Schluss gesetzt wird, erhalten wir eine Lösung mit "Summe der Anschlussintervalle = null(0)", was offensichtlich minimal ist:

   . . .

   . . .

   M O

   O M

   M U

   U M

6. Alternativ kann es auch davor gesetzt weren, und liefert ebenfalls eine solche Lösung:

   . . .

   U M

   M O

   O M

   M U

7. Setzen wir nun, dass MO-OM irgendwo aufträte, aber nun nichts darauf folgte:

   . . .

   . . .

   M O

   O M

8. Dann kann (wie oben) nur UM mit dem Anschlussintervall null(0) davorgesetzt werden:

   . . .

   U M

   M O

   O M

9. Das führt zur Lösung:

   M U

   U M

   M O

   O M

10. Damit sind alle Möglichkeiten für das zu Beginn gesetzte MO erschöpft. Nehmen wir alternativ MU mit dem Nachfolger UM als Ausgangspunkt, so ergeben sich die invertierten Lösungen:

    M U	U M	M O	O M
    O M	M U	U M	M O
    M O	O M	M U	U M

    
    Von diesen ist nur die zweite neu.

Insgesamt ergeben sich also die Lösungen

Es gelten die Symmetrien:

1. in allen Lösungen ist die zweite Hälfte das I der ersten.
2. 1 und 3 sind ihre gegenseitigen Is
3. 2 und 4 sind ihre gegenseitigen Is
4. 1 und 3 gehen auseinander hervor durch Vertauschung der Hälften.
5. ebenso 2 und 4.
6. 2 und 4 sind ihr eigenes R.
7. Also ist in 2 und 4 das R der ersten Hälfte gleich der zweiten.

^{^Inh} 5 Historische Verwendung der aufgewiesenen Techniken und Materialien

Ein sehr prägnantes Beispiel für Teilreihen, die gegenseitig ihre Modi sind, findet sich in der Fuge der C-Dur Violinsonate von J.S.Bach:

Abbildung 9: Interne Reihenoperation im Fugenthema der C-Dur-Violinsonate von Bach

Der Einsatz der Umkehrung des Gesamtthemas in Takt 202 beginnt die zweite Hälfte des Satzes (im goldenen Schnitt). Ein fundamental wichtiger Effekt für die motivische Entwicklung und das formale und inhaltliche Empfinden ist nun, dass Takt 4 des Gesamtthemas "T" die Umkehrung von Takt 1 ist, siehe zweite und dritte Notenzeile. Wir haben hier also unseren Grundfall vorliegen, dass zwei Teilreihen gegenseitig durch eine dodekaphone Operation (hier "I") aus einander hervorgehen. Dies alles selbstverständlich unter den Rahmenbedingungen der tonalen, diatonischen Setzweise.

Also wirkt die Bildung I(T) der Umkehrung des Gesamtthemas teilweise/unter anderem wie eine Permutation seiner Elemente P(T), symbolisch:
I(x;..;ix) = ix;..;x = P(x;..;ix)

Beim Hören von Takt 202 hat man den originalen Themeneinsatz Dutzende Male gehört, -- der Einsatz der I-Form ist ein deutlicher Einschnitt, auch vordergründig. Das vermeintliche Wiederauftreten der A-Form in Takt 205 wirkt fast wie ein Ruck, wie ein Filmschnitt, als eine fast brutale Verstörung.

Diese Wahrnehmungsweise und Wirkung wird unterstützt (a) durch den Eingriff in den Rhythmus von Takt 3, Verschiebung der Achtelbewegung bei gleicher Tonfolge, der den Auftakt von Takt 1 und 205 stärker angleicht; (b) dass Takt 205 eine Quinte höher erklingt als 1, also im traditionellen Fugenabstand, (c) das auch Takt 2 und 204 (nach erwähnter Rhythmus-Anpassung) in einem ähnlichen Verhältnis stehen, also ebenfalls als Permutation "missverstanden" werden können, siehe Notenzeilen zwei und vier.

Für diesen Satz, dessen Fugenthema beginnt wie der Choral "Komm Heiliger Geist, Herre Gott" (vgl. die Fantasia sopra... BWV 651, siehe unterste Notenzeile) sind diese Satz- und Wahrnehmungsverhältnisse wohl auch inhaltlich konstitutiv.

Wie erwähnt eignen sich unsere Grundhaken, als die minimalen voll-modalen Materialien, vorzüglich als Ausgangsmaterial von All-Modi-Reihen. Diese Kombination kann man in voranstehendem Beispiel schon erkennen, z.B. Takt 1 ohne Auftakt als Haken OM=O-U-M.

Noch deutlicher findet sie sich in Kunst der Fuge, Cp X (nach der Gräserschen Zählung). Dieser ist eine der Fugen mit Kontrasubjekt im doppelten Kontrapunkt, hier der Dezime. Das Hauptthema taucht nur in der Umkehrung auf. Das Kontrasubjekt wird hingegen im Expositionsteil, noch ohne Hauptthema, dreimal exzeptionell in der Umkehrung gebracht, -- vielleicht, um psychologisch das Einsetzen des umgekehrten Hauptthemas vorzubereiten.

Die ersten sechs Noten des Kontrasubjektes sind genau unsere Haken MU (=M-O-U) und MO (=M-U-O), die gegenseitig ihr I sind. Ab Takt 14 treffen Original und Umkehrung des Kontrasubjektes (A und I) in Alt und Tenor in Engführung aufeinander, und der Sopran als freier Kp vermittelt zusätzlich durch einen freien Haken:

Abbildung 10: Haken-Motive in der Kunst der Fuge

Das deutlichste und dieses Projekt seinerzeit motivierende Beispiel ist aber das Konzert op. 24 von Anton Webern (1934):

Abbildung 11: All-Modi-Reihe in Webern, Konzert op.24

Selbstverständlich haben "Zwölftonreihen" als Reihen von Tonhöhen-Klassen im engeren Sinne überhaupt keine eindeutige eigene Kontur, da jedes Intervall ja modulo Oktave nach oben oder unten versetzt gelesen werden kann.

In besagtem Beispiel jedoch bilden zunächst die Schreibweisen mit minimalem Ambitus eindeutig eine Hakenreihe, siehe zweite Notenzeile.

Aber auch die Satzweise, die Webern konkret anwendet, zeigt, jedenfalls am Satzbeginn, siehe erste Notenzeile, eine (andere) Hakenreihe. Diese ist wegen der immer gleichartigen Oktavversetzung eindeutig als solche gemeint!

Die Reihe OMMU;MOUM=N-;e ist aus der IR-Menge, jeder Doppelhaken/jede Halbreihe also mit IR-Symmetrie. Allerdings herrscht Zeilensprung, sodass die Gesamtreihe keine Symmetrie aufweist. R und IR angewendet auf die Gesamtreihe erscheinen deshalb teilweise wie Permutationen "P".

Fast wie ein duales Gegenbeispiel wirkt das Streichquartett op. 28 desselben Komponisten (1939) mit folgender (transponierten) Reihe:

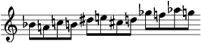
Abbildung 12: Punktsymmetrische Reihe in Webern, Streichquartett op.28

Hier hat die Teilreihe vier(4) Anschläge, passt also nur dreimal in die Gesamtreihe. Sie hat aber auch nur zwei(2) verschiedene Modi, da sie IR-symmtrisch (punktsymmetrisch) ist. Also kann eine ihrer Instanzen in die Mitte gestellt werden, und zwei identische nach vorne und hinten, sodass die Gesamtreihe IR-symmetrisch wird. In der Mitte steht selbstverständlich der andere, im Vergleich zum äußeren I-gespiegelte (R-gespiegelte) Modus. Die Teilreihe ist die berühmte Signarur-Sequenz "B-A-C-H".

---

Abbildung 13: Hakenmotive in Hufschmidts Sämann

In Wolfgang Hufschmidts Motette Der Sämann aus den Vier Gleichnissen (1962) besteht die Reihe aus zwei verschobenen Ganztonleitern. Von einer "Reihe" im Sinne der reinen Lehre der Dodekaphonie kann nicht die Rede sein. Interessant ist die Hakenstruktur: die Reihe ist meist "in Phase" mit dem Ablauf in Dreiergruppen abgeteilt, die in ihrer normalen, engsten Anordnung OM-Haken bilden. Um zwei Positionen verschoben (siehe Text "Da er DAS SAGTE") ergibt sich der Haken MU. Durch Oktavversetzung kann OM in MU ("zu säen") verwandelt werden, und MU in OM ("Da er das", dritte Notenzeile).

Diese Operationen werden im Werk zwar nicht systematisch durchgeführt, sind jedoch allemal für die Ableitung des melodischen Materials fundamental.

---

In des Verfassers Faust-Opern taucht ab der "Hexenküche" diese Zwölftonreihe auf: FIXME MENGENBILDUNGSNUMMER (DIESELBE WIE OBEN) = 3 (gis h c)

Abbildung 14: All-Modi-Reihe in Faust-eins-eins / Hexenküche

Sie ist bewusst nicht all-modal. Das zweite System zeigt die naheliegende Korrektur in eine IR-symmetrische Hakenreihe.

Die ersten zwei Dreiergruppen werden allerdings am Beginn deutlich exprimiert, was sich in der Rezeption auf die zweite Hälfte der Reihe überträgt, und den tatsächlich erklingenden trivialen Echos von Klein-Sekund-Seufzern (d-cis, dann g-fis, dann b-a) durch hemiolische Anmutung interessanter macht. Konstruktiv ausgebeutet wird nämlich im Kontext dieses Werkes die tonale/funktional-harmonische Struktur dieser Tonfolge (z.B. der Schluss als dominantisch zum Anfang), die also eher als "zwölftönige Melodie" zu verstehen ist und dadurch nur eine gewisse Aura von "wissenschaftlichem Hexenwerk" transportieren soll. Dennoch werden alle dodekaphonen Operationen durchaus konstitutiv eingesetzt.

^{^Inh} 6 Konstruktive Verwendung von Haken im voll-seriellen Kontext

^{^Inh} 6.1 Parameter-Polyphonie. Mögliche Kompositionsverfahren

Nach obigen rein abstrakten Herleitungen der grundlegenden Eigenschaften des Materials (Modi und Anschlussintervalle von Haken, Doppelhaken, Hakenreihen) sollen nun die konkreten Wirkungen auf Rezipienten untersucht werden, wenn dieses auf verschiedenste Art in verschiedenartigsten Medien dann tatsächlich umgesetzt wird. Diese Untersuchung soll durch praktische Erprobung geschehen. Dazu dient ein erstes Studien-Projekt HKN_v00, welches in Kapitel 7 vorgestellt wird. Dieses Kapitel bringt zunächst grundlegenden Überlegungen.

Voranstehende Beispiele zeigten solche Umsetzungen im barocken und dodekaphonen Kontexten. Wesentlich weitergehende Möglichkeiten zur praktischen Erprobung bietet allerdings die voll-serielle Kompositionsweise (wie oben definiert, siehe Kapitel 1). Dort ist es nämlich grundlegend, einen (im Vordergrund "einfachen") einstimmigen klingenden Verlauf in sich schon als Polyphonie seiner Parameter aufzufassen. Eine Folge von Haken kann somit bei z.B. einem Viola-Solo die Tonhöhen bestimmen, eine andere die Lautstärke, eine dritte die Artikulation, etc.

Dabei ist notwendig, wie ganz zu Beginn für unsere Haken im allgemeinen gefordert, dass für all diese Parameter Ordnungen definiert sind, die "unten, mitte, oben" nicht nur theoretisch festlegen, sondern auch vom Rezipienten einfach und eindeutig wahrnehmbar machen.

Grundsätzlich kann mit dem bisher abgeleiteten Haken-Material auf dieselben Weisen "komponiert" werden wie mit herkömmlichem, also Tonhöhenverläufen, etc. Verschiedene Möglichkeiten dazu sind (a) ein algorithmischer Ansatz, wo die Hakenfolgen bereits als solche das Ergebnis der Auswertung einer Rechenvorschrift sind, angewandt auf Eingabedaten in einem dritten, noch weiter abstrahierten Format.

^{^Inh} 6.2 Partiturbasierte Komposition von Hakenverläufen

Da es uns ja zunächst um eine systematische Erforschung der Eigenschaften und des Verhaltens des Materials als solchem geht, wählen wir die Möglichkeit (b), schreiben also "polyphone Sätze von Hakenfolgen" ausdrücklich hin.

Ein und dieselbe Hakenfolge soll dann in verschiedenartigste Vordergrund-Formate übersetzt werden, also in konkrete Instrumentalbesetzungen oder andere realisierende Ausführende. Für die Übersetzung der abstrakten Hakenfolge in deren Notenmaterial sollen verschiedenartige Regeln und Verfahren ausprobiert werden.

Den für die Realisierung ("im Vordergrund") sich letztlich ergebende Notentext und seine klanglichen Umsetzung nennen wir Vordergrund-Stimme oder V-Stimme; deren Ereignisse Vordergrund-Ereignisse oder V-Ereignisse.
Die verschiedenen Haken-Verläufe, betrachtet als komponierte musikalische Stimmen, nennen wird Konstruktions-Stimme oder K-Stimme und die in ihnen notierten Ereignisse Konstruktions-Ereignisse oder K-Ereignisse.
Ebenso dann K- und V-Partitur, K- und V-Zeitpunkt, K-Pause und V-Pause, etc.
Die Erzeugung von V-Stimmen aus K-Stimmen heiße "Übersetzung".
Diejenigen Parameter einer V-Stimme, die tatsächlich aus Haken einer K-Stimme abgeleitet werden, heißen "Hakenparameter".

Die drei Wertestufen, die eine Haken ausmachen, weiterhin mit "O", "M" und "U" bezeichnet, nennen wir "RelWert", für "relativen Wert". Ein und derselbe RelWert wird in verschiedenen Parametern je anders umgesetzt.

^{^Inh} 6.3 Notation und Realisierung von Hakenverläufen mit tscore

Grundlage unserer weiteren Untersuchungen ist eine auf der BandM-Partitursprache "tscore" basierende Implementierung, weil die Voraussetzungen und Konsequenzen der einzelnen Entscheidungen am einfachsten durch praktische Experimente gefunden und vermittelt werden. Diese werden durch automatische Übersetzung und automatische Generierung der V-Partiturdaten durchaus beschleunigt. (Dies macht einen erheblichen Unterschied zum "ersten Anlauf" vor fast vierzig Jahren, der vielleicht deswegen scheitern musste, siehe Kapitel 8.)

tscore ist ein generisches Textformat (und seine Implementierung) zur Eingabe von beliebigen zeitbasierten Werteverläufen in einem vom Benutzer frei zu definierenden Partiturformat, ausführlich beschrieben in [tscore], das ist die tscore Benutzer-Dokumentation.

Die Syntax der Eingabe ist allemal dieselbe, egal wie die Umsetzung der Hakenverläufe aussehen soll. Diese Syntax und die ersten Verarbeitungsschritte der Partiturdaten sind definiert in der Java-Klasse Score_hkn.java, siehe deren API-Dokumentation und deren Quelltext.

Diese Syntax ist recht einfach und orientiert sich an der Akkoladen-Struktur der herkömmlichen Partituren der "Common Western Notation", also der traditionellen eurozentrischen Notation, und ist weitgehend intuitiv verständlich. Deshalb wird sie im folgenden auch verwendet, um die ersten noch rein theoretischen Überlegungen zu illustrieren.

tscore erlaubt das "Einstöpseln" der unterschiedlichsten Zeitmodelle und Parsierungsregeln für die Notation zeitlicher Abhängigkeiten. Zur Zeit verfolgen wir im HKN-Projekt nur einen einzigen Ansatz, gennannt rein-relative Abfolge, im folgenden genauer erklärt.

Ist eine in tscore geschriebenen K-Partitur einmal von der Infrastruktur übersetzt, kann aus der resultierenden Datenstruktur je nach aufgerufenem Code eine Partitur für das gewünschte Vordergrund-Format gewonnen werden.
Diese unterschiedlichen "Semantiken" werden z.Zt. durch "hart-codierten" Java-Text bestimmt und realisiert, -- Ziel der Untersuchung ist es u.a. auch, eine passende abstrahierende Sprache dafür zu finden, um den Anwender weiter zu entlasten. Es kann allerdings jetzt schon gesagt werden, dass dieser Code-Anteil für die meisten Vordergrund-Formate sehr gering ist, und die tscore-Infrastruktur schon eine weitgehende Konzentration auf das Nötige unterstützt, siehe die im folgenden verlinkten Quelltexte.

^{^Inh} 6.4 Rein-Relative Abfolge der K-Ereignisse

Für das Verhältnis von K-Ereignissen zu V-Ereignissen und zu der in der V-Partitur ablaufenden Realzeit lassen sich theoretisch verschiedene Festlegungen treffen.

Die erste Möglichkeit (und die einzige, die im folgenden ausgeführt wird) nennen wir rein-relative Abfolge. Sie enthält folgende Festlegungen:

KV-0:
Die K-Partitur enthält die Ereignisse in den verschiedenen K-Stimmen in beliebiger Gleichzeitigkeit oder Verschiebung. Ein K-Ereignis ist dabei der abgekürzte Name entweder eines RelWertes oder eines Hakens (ein oder zwei Großbuchstaben, siehe oben Abschnitt 4.1) oder eines Doppelhakens (drei oder vier Großbuchstaben, siehe unten Abschnitt 6.7).
(K-Pause heißt zunächst nur rein syntaktisch, das nichts dergleichen dort steht, -- dies kann je Übersetzungsregeln unterschiedliches bedeuten.)

KV-1:
Jedes K-Ereignis "entspricht" einem V-Ereignis. (Zur Begründung: jedes K-Ereignis als "Ergebnis einer kompositorischen Entscheidung" soll sich direkt in einem konkret klingenden Ereignis der V-Stimme widerspiegeln.)
Genauer:
Alle synchron notierten K-Ereignisse, und nur diese, entsprechen demselben V-Ereignis.
Die relative Reihenfolge der V-Ereignisse in der generierten Umsetzung respektiert die relative Reihenfolge der zugrundeliegenden K-Ereignisse.
Die RelWerte des K-Ereignisses bestimmen unmittelbar die Parameter des V-Ereignisses.

Daraus folgt aber wegen der "Freiheit des Satzes" in den K-Stimmen:

KV-2:
Einem durch KV-1 erforderten V-Ereignis entspricht nicht unbedingt ein K-Ereignis in jeder Hakenstimme, also für jeden Hakenparameter.

Dazu später mehr; zunächst die Alternativen für die V-Zeitpunkte.

KV-3:
Bei der "rein-relativen Abfolge" der K-Ereignisse bestimmt die K-Partitur nur die relative Anordnung, wie ausgeführt. Die Bestimmung der konkreten Zeitpunkte der Ausführung der V-Ereignisse erfolgt anders, z.B. improvisatorisch, oder durch einen Hakenparameter der "Dauer" oder "Einsatzabstand" bestimmt, oder durch konstantes "nullgestelltes" Pulsieren, etc.

(Man kann auch sagen: Die "T"-Zeile der K-Partitur und die darin auftretenden "Taktnummern" haben bis auf die relative Lage der K-Ereignisse zueinander keinerlei Bedeutung.)

KV-4:
Im Gegensatz dazu ist eine "zeitgenaue K-Partitur" denkbar, wo die K-Ereignisse wie traditionelle Noten mit einen metrischen oder physikalischen Zeitangaben notiert werden, die unmittelbar auf die entsprechenden V-Ereignisse übertragen werden.
tscore würde deratige Verfahren ohne große Schwierigkeiten ermöglichen, sie werden aber im folgenden nicht durchgeführt und bleiben einer Weiterentwicklung überlassen.

KV-2 oben besagt, dass bei einer "absolut freie polyphone Schreibweise" vereinzelte K-Ereignisse auch auftreten dürfen, ohne dass in den parallelen K-Stimmen auch ein synchrones K-Ereignis steht. Diese K-Ereignisse können Haken entsprechen, deren Verläufe nun gegeneinander gesetzt werden müssen. Weiterhin benötigt ein V-Ereignis zu seiner Realisierung (normalerweise) ausnahmslos alle seine Parameter. Also müssen die zur Generierung der V-Ereignisse nötigen Parameterverläufe entsprechend aufgefüllt und synchronisiert werden.

Wir nennen die erste Phase der Umsetzung Expandierung. Diese ist unabhängig vom gewählten V-Format, nur abhängig von den dafür ausgewählten K-Stimmen. Am Ende erhalten wir für jede von diesen eine Folge von RelWerten, in denen die von K-Ereignissen geforderten Haken in Folgen von Rel-Werten expandiert sind. Dies geschieht so:

KV-5:
Sei SumKZP die Summe der K-Zeitpunkte, also die Menge aller Zeitpunkte der K-Partitur, an welchem in mindestens einer K-Stimme ein Ereignis steht. Bei der Umsetzung wird zunächst SumKZP bestimmt. Jeder Zeitpunkt daraus entspricht (im letztlichen Resultat der Umsetzung) genau einem V-Ereignis. Sei kA ein K-Ereignis das in einer gegebenen Stimme eine Angabe trägt, und sei kN das nächstfolgende Ereignis derselben Stimme mit ebenfalls einer expliziten Angaben.

KV-6:
Trägt kA eine RelWert-Angabe, so wird dieser Wert auf die Folge aller Zeitpunkte aus SumKZP bis (ausschließlich) kN übertragen. (Dies geschieht zunächst als "schwacher RelWert", in den Beispielen mit Kleinbuchstaben bezeichnet, um ihn von den expliziten K-Ereignissen evtl. noch unterscheiden zu können, wie weiter unten ausgeführt.)

KV-7:
Ist K-Ereignis kA eine Hakenangabe, dann werden auf die Folge aller Zeitpunkte aus SumKZP bis (ausschließlich) kN die drei RelWerte des Hakens "möglichst äquidistant" verteilt, wobei Distanz gemessen wird in Anzahl abstrakter K-Ereignisse in SumKZP.

 T       1         2        3        5
 VOX a   M         M        M        M  // Vox a fordert K-Ereignisse

 VOX b   MO                          M  // abst=3, ausreichend Platz
//       M         U        O        M

 VOX c   MO                 O           // abst=2, ausreichend Platz wg. Überlp.
//       M         U        O        o

 VOX d   MO                 M           // abst=2, keine Überlappung, ein(1) 
                                        //   K-Zeitpunkt muss synthetisiert werden
//       M    U    O        M        m     erste Möglichkeit
//       M         U    O   M        m     zweite Möglichkeit


 VOX e   MO        O                    // abst=1, nur ein(1) Zeitpunkt muss 
//       M    U    O        o        o      synthetisiert werden, dank Überlappung

 VOX f   MO        M                    // abst=1, zwei(2) Zeitpunkte müssen 
//       M  U   O  M        m        m         synthetisiert werden

KV-9:
Eine wichtige Modifikation ist, dass der letzte Wert eines Hakens nicht eigens dargestellt werden muss, wenn sein Wert identisch ist mit dem Wert des nächsten Ereignisses (entweder konstanter RelWert oder Beginn des nächsten Hakens). Das entspricht der "Auslöschung" oder "Überlappung" genannten Technik in der klassischen Dodekaphonie. In Stimme "c" in Abbildung 15 ist deshalb ausreichend Platz, nur "M" und "U" müssen dargestellt werden.

Ist der Abstand nur =1, dann muss im Falle der Überlappung einer, sonst zwei K-Zeitpunkte eingefügt werden, siehe Stimmen e und f.

Problematisch ist Fall "d", wenn nur ein Zeitpunkt gegeben ist, zwei aber benötigt. Dann gibt es nämlich zwei verschiedene Möglichkeiten der Einfügung.

Die tscore-basierte Lösung entscheidet wie folgt:
KV-10:
Zunächst werden allen eindeutig notwendigen Zeitpunkte nach Fall e und f generiert, und die damit zusammenfallenden Anforderungen nach Fall d gleichzeitig als erledigt abgehakt.

KV-11:
Die noch übrigbleibenden Anforderungen gemäß Fall d zerfallen in zusammenhängende Unterfolgen von möglichen Einfügungsstellen. In diesen Folgen wird jeweils auf den geradzahligen Positionen die Einfügung durchgeführt, das dies deren Anzahl minimiert, siehe folgendes Beispiel:

    T       1         2         3        4        5       6
    VOX a   M         M         M        M        M       M
                 ?       ?          ?        ?        ?
    VOX b   MU                  M
    VOX c             MU                 M
    VOX d                       MU                M
    VOX e                                MU               M
// expandiert zu
    VOX b   M         O  U      M
    VOX c             M  O      U        M
    VOX d                       M        O   U    M
    VOX e                                M   O    U        M

KV-12:
Ein Apostroph kann vor jedes K-Ereignis gesetzt werden um eine Überlappung explizit zu verbieten. Das erlaubt, Folgen nur von Haken in allen Stimmen gegeneinanderzusetzen und diese immer mit allen drei(3) Werten erklingen zu lassen, ohne die die Notwendigkeit von "Stützereignisse", wie in obigen Beispielen jeweils die "VOX a".

Wie oben erwähnt braucht jedes V-Ereignis immer alle Hakenparameter zu seiner Realisierung. Fall ihm nicht in jeder Stimme ein K-Ereignis entspricht, gibt es mehrere Methoden, dies auszugleichen:

KV-13:
Bei der Prolongationsmethode werden sowohl die expliziten RelWert-Angaben als auch die Werte der Haken nach ihrer Aufteilung einfach fortgeschrieben. Die "schwachen" RelWerte (gemäß obenstehendem Algorithmus) werden also genauso umgesetzt wie die explizit in den K-Ereignissen angegebenen.

KV-14:
Als Alternative gibt es die Interpolationsmethode, bei der die "starken" RelWerte genauso angeordnet werden (also explizite RelWert-Angaben oder die Anfänge der drei Hakensegmente), aber zwischen ihnen statt einer Wiederholung ein Überblendungs-Prozess eingefügt wird. Dieser kann linear, exponentiell, etc. unterschiedlich definiert sein. Die "schwachen" RelWerte tauchen hier als solche also nicht auf, sondern "sind unterwegs".
Die Erkennbarkeit der Hakenkonturen für einen Zuhörer kann dadurch erheblich verbessert werden, aber die Umsetzungsalgorithmen werden deutlich komplizierter und differenzierter.

Z.Zt. wird im HKN_v00-Projekt nur die Prolongationsmethode unterstützt, die Implementierung kennt keine "schwachen" RelWerte.

Warnung:
Eine böse Falle besteht in der Tatsache, dass die einzelnen K-Stimmen tatsächlich "VOX"-Konstrukte im Sinne von tscore sind [tscore].

Die Textspalten sind zwischen ihnen nicht reliert, -- jede VOX teilt bezieht sich nur auf die "T"-Zeile und teilt die dort definierten Spaltengruppen gleichmäßig, für sich.
Verwechselt man das Verhalten dieser verschiedenen VOXes mit der in tscore eine Ebene tiefer ja möglichen verschiedenen "Parameter-Tracks" derselben Stimme, dann kann man irrigerweise meinen, die unter (A) aufgeführte Partitur ergibt die Expandierung (D). Sie ergibt aber (B), da (A) und (A') identisch sind, wobei (A') die zeitliche Zerlegung des Intervalles "1=>2", eimal durch zwei(2), dann durch drei(3), besser wiedergibt.
Wenn man (D) will, kann man (u.a.) wie bei (C) notieren:

(A)                        (A')                          (B)                         
  T      1           2       T      1               2     T      1               2    
  VOX a  O   M       U       VOX a  O        M      U     VOX a  O   O   M   M   U 
  VOX b  U   O   M   U       VOX b  U    O       M  U     VOX b  U   O   O   M   U

(C)                                                       (D)                         
  T      1   !       2                                     T      1           2    
  VOX a  O   M       U   	                           VOX a  O   M   M   U 
  VOX b  U   O   M   U      	                           VOX b  U   O   M   U

^{^Inh} 6.5 Parameter-Interne Polyphonie. Mehr als drei V-Parameter-Stufen

   VOX  a  UM              X
   VOX  b  UM   UM   UM    X
        Vordergrundgestalt:    Auftreten der Wertstufen:
4  ____                        1
3  ____          /\            2
2  ____         /     /\       3
1  ____     /\       /         2
0  ____    /                   1

6  ____                        1
5  ____         /\             1
4  ____        /               2
3  ____               /\       1 
2  ____              /         2
1  ____     /\                 1
0  ____    /                   1

8  ____                        1
7  ____        /\              1
6  ____       /                1
5  ____                        1
4  ____               /\       1
3  ____              /         1
2  ____                        1
1  ____     /\                 1
0  ____    /                   1

Das vorliegende Beispiel-Projekt HKN_v00 unterstützt die erste obenstehende Variaten mit fünf Wertstufen im V-Format "Vla", siehe Abschnitt 7.3.

^{^Inh} 6.6 Explizite Pausen und Gliederung

Bei konkreten Experimente mit der tscore-basierten Implementierung stellte sich bald heraus, dass explizite Pausen und Gliederungselement sehr zweckmäßig sind, um nachvollziehbare ästhetische Prozesse gestalten zu können: um die Hakenformen zumindest "initial", zur "Einstimmung der Rezeption" deutlich als solche erkennen zu können reicht ihre eigene reine Wertefolge nicht aus, sondern "grobe Maßnahmen" wie durch äußere Mittel dargestellte, unüberhörbare Gliederungsgrenzen müssen darüberhinaus zum Einsatz kommen.

Dazu kann in der tscore-Partitur eine K-Stimme mit Pausenangaben als ihren Ereigniswerten definiert werden, und dann für den Übersetzungsdurchlauf als "Pausenstimme" selektiert. Die K-Ereignisse "p0", "p1", "p2", ...stehen dabei für zunehmend längere Pausen, die vor dem K-Ereignis (also: vor dem ersten dem K-Ereignis entsprechenden V-Ereignis) in die V-Stimme eingefügt werden.

Eine Pausenstimme ist also zu lesen wie eine gliedernde Überschrift: mit diesem K-Ereignis beginnt eine neue Sinn-Einheit, und diese wird durch eine Pause entsprechder Länge vom vorangehenden Klang abgesetzt.

^{^Inh} 6.7 Doppelhaken

Soll gegen eine Folge von Doppelhaken nun ein augmentierter gesetzt werden, so kann es sein, dass die Notation des exakten Beginnes des zweiten Hakens nicht möglich ist. Folgender Quelltextausschnitt zeigt die verschiedenen Varianten der allerersten Einsätze aus der Studie HKN_v00/vox_drei_doppelhaken.haken (mit den Übersetzungen HKN_v00/vox_drei_doppelhaken_0.pdf und HKN_v00/vox_drei_doppelhaken_1.pdf), wie ausführlicher besprochen unten in Abschnitt 7.2.

Die Schreibweisen für Doppelhaken mit und ohne interner Überlappung sind intuitiv verständlich. Abbildung 19 zeigt die verschiedenen Schreibweisen mit und ohne Doppelhaken und ihre Expanierungen.

// vgl. prinzipiell "vox_drei_doppelhaken.haken" :

// frühere Schreibweise vor Einführung der Doppelhaken, nicht ganz genügend:
    T             10       !   !     !        20        /*...*/ 30
    VOX v1_pause  -        p2        p2       p3 
    VOX v1_0      OM MU    'UM MU    'UM MO   'OM  MU   /*...*/
    VOX v1_1      OM           ~MO            UM
// oder:
    VOX v1_1      OM~          MO
// expandieren beide zu
//                oum ou   uo  mou    uom uo  oum ou
//                ooo uu   uu 
//                             mmm    uuu oo  |... 
//              => etwas unregelmäßig !!


    VOX v1_0      OM MU    'UM MU    'UM MO   'OM  MU   /*...*/
    VOX v1_1      OMO                         UMU
    VOX v1_1      OMO                         OMO
// expandieren beide zu
//                ooo uuu    mmm    uuu  ooo  |...
//              => no overlap und vollkommen gleichverteilt

    VOX v1_0      OM MU    'UM MU    'UM MO   'OM  MU   /*...*/
    VOX v1_1      OMMO                        UMU
// expandiert zu
//                oo  uuu   mm  mm uuu oo     |... 
//              => no overlap und fast regelmäßig (von innen nach außen wachsend)

    VOX v1_0      OM MU    'UM MU    'UM MO   'OM  MU   /*...*/
    VOX v1_1      UMU~                        UM
    VOX v1_1      UMU                         ~UM
// expandieren beide zu
//                uuu    oooo     mmmm oooo   |...
//              => does overlap und fast regelmäßig (von innen nach außen wachsend)

    VOX v1_0      OM MU    'UM MU    'UM MO   'OM  MU   /*...*/
    VOX v1_1      UMMU~                       UM
    VOX v1_1      UMNU                        ~UM
// expandieren beide zu
                  uuu    ooo   mmm   mmm  ooo |...
                => does overlap und vollkommen gleichverteilt

Aus kompositorischer Sicht scheinen die Varianten "OMO" und "UMMU~" wohl beide sehr wünschenswert, und beide sind durch Reihung von einfachen Haken nicht darstellbar, wegen der verschobenen Lage zur anderen Stimme.

Für die Stimme "v1_0" dürfen allerdings keine Doppelhaken genommen werden; in der derzeitigen Implementierung müssen zwei einzelne geschrieben werden, mit impliziter oder expliziter Überlappung. Ein wichtiger Unterschied ist nämlich der, dass keine automatische Zeitpunkt-Synthese erfolgt, -- der Platz für den Haken muss also ausreichend sein. Das einzige was automatisch erfolgt ist die Generierung einer Überlappung, falls das für die Darstellung nötig ist.

Dies ist deshalb so entschieden, weil uns bis jetzt kein Regelwerk eingefallen ist, welches die verschiedensten polyphonen Möglichkeiten von Doppelhaken mit ihren vier bis sechs impliziten Stützwerten auf ähnlich einfache, eindeutige, dem Benutzer nachvollziehbare und ästhetisch sinnvolle Weise expandieren würde wie das für einfache Haken definierte, siehe oben Abbildung 15 und Abbildung 16.

^{^Inh} 6.8 Mögliche Erweiterungen

(1)
Das Zeitmodell und die Syntax der "T-Linie" könnte auch so gewählt werden, dass die K-Ereignisse direkt die Zeitpunkte der V-Ereignisse angibt (resp. des jeweils ersten V-Ereignisses für jedes hakenförmige K-Ereignis). Dies könnten sowohl physikalische Sekundenwerte sein, als auch musikalisch-metrische im CWN Sinne, o.ae.
Die Expandierung der Haken zu mehreren K-Ereignissen würde komplizierter, weil die Proportionen der Teilung dann eine Rolle spielen, im Gegensatz zum "rein-relativen" Verfahren. Ausserdem kann "Dauer" dann wohl schwerlich noch Hakenparameter sein.

(2)
Abstrakte Haken und Doppelhaken können auch "verzerrt" auf eine Werteskala abgebildet werden, also unter Auslassung einiger Stufen. (Diese Idee tauchte erst wieder auf bei der Durchsicht der historischen Skizzen, s.u.) Dies ergibt in der optischen Erscheinung charakteristische "Bockshörner". Es wird aber in der Rezeption erst wirklich deutlich im Zusammenhang mit sequenziert anschließenden Nachbar-Haken, weil dann neue Stufen erklingen, die zuvor als "Lücken" nur vermutet werden konnten:

  7__      x       x
  6__    x/ \     / \x   x       x    
  5__        \   /     x/ \     / \x   
  4__         \ /          \   /      
  3__          x            \ /         
  2__		             x        

^{^Inh} 7 Eine erste Studiensammlung "HKN_v00"

^{^Inh} 7.1 Konzept und Grundlegendes

Das kleine Beispiel-Projekt HKN_v00 besteht aus verschiedenen K-Partituren und je verschiedenen Übersetzungen. So entstehen V-Partituren für vier solistische Vordergrund-Formate. Diese sind Vox=menschliche Stimme, Vla=Viola, Sig=elektronische Realisierung und Svg=graphische Realisierung.

Darin sind eher generische K-Partituren, aus denen verschiedene V-Partituren entstehen durch Anwendung unterschiedlicher Übersetzungen, aber auch andere, die speziell für ein bestimmtes V-Format geschrieben sind.

Jede solche V-Partitur wird als ein "Satz" bezeichnet; eine Aufführung besteht aus einer Anordnung dieser Sätze, die ganz oder in Teilen ablaufen können, dabei an andere Sätze anschließend, überlappend oder gar gänzlich gleichzeitig. Es können neben den "fest notierten" Teilen auch durchaus improvisatorische, reaktive eingebaut werden. All diese Entscheidungen liegen bei den Interpreten.

Jeder der vier Vordergrund-Formate kennt unterschiedlich viele Hakenparameter. Die Werte der übrigen, technisch notwendigen Parameter sind dabei in den V-Partituren jeweils (a) als unveränderlicher Konstantwert vorgeschrieben ("nullgestellt") oder (b) spontan komponiert, in rein unterstützender Rolle, oder (c) dem Interpreten zur improvisatorischen Gestaltung überlassen.
Die Hakenparameter lassen sich wie folgt gruppieren:

Bemerkenswert ist, dass die klassischen seriellen Parameter Tonhöhe, Dauer und Laustärke nur insgesamt vier mal auftreten, bei vierzehn Hakenparametern insgesamt.

Die Tonhöhe ist immer entweder konstant oder auf wenige Stufen reduziert (von möglichen improvisieren Abweichungen abgesehen, wie oben beschrieben.) Diese Tonhöhen sollen einen "schwebenden" Gesamtklang hervorbringen, immer wenn alle V-Formate zusammenklingen:

Abbildung 21: Disposition der Tonhöhen in der ersten Kompositionsstudie HKN_v00

Im folgenden finden sich Verknüpfungen zu den K- und V-Partituren dieser ersten Komposition HKN_v00. Dabei sind die V-Partituren verschiedene Umsetzungen der K-Partituren, wie aus dem Makefile hervorgeht.

Diese enthalten im Stile von "literate Programming" ausführliche Dokumentationstexte, und damit nicht nur die Herleitung des getroffenen Entscheidungen, sondern auch weitere Aussagen über die Haken, ihre Struktureigenschaften, über Verwendungs- und Kombinationsmöglichkeiten.

Manche dieser Ergebnisse ließen sich auch mit viel Gewinn für den Leser in den voranstehenden Allgemeinen Teil zurückübertragen. Dies haben wir bewußt nicht getan, denn, wie erwähnt, ist dieses Kompositionsprojekt gleichermaßen ein Forschungsprojekt, und die Darstellung direkt in der Partitur macht Wege und Irrwege nachvollziehbar.

Die Realisierungen aller oben genannten Übersetzungen geschieht durch Java-Klassen, die von einer Basisklasse Score_hkn abgeleitet sind; hier der Quelltext.

Diese Basisklasse implementiert das immer Gleiche, nämlich das Parsieren der tscore-HKN Partituren. Wie in allen tscore-Kontexten üblich werden diese in ein Objekt der Klasse TimeScape übersetzt, siehe auch die tscore Benutzer-Dokumentation.
In einem zweiten Schritt kann der Benutzer (= der spezielle Code der abgeleiteten Klasse) dann ein Expansion-Objekt erzeugen, welches die Synchronisierung und Auffüllung explizit ausgewählter K-Stimmen vornimmt und alle auftretenden Haken in Folgen von RelWerten übersetzt, siehe die Diskussion oben in Abschnitt 6.4.

Von dieser allgemeinen Klasse leiten die Implementierungen der verschiedenen Vordergrund-Formate ab.

^{^Inh} 7.2 Version "Vox" für Stimme Solo

Die Implementierung befindet sich in Score_hkn_vox_v00.java (API-Dokumentation), eine abgeleitete Klasse, die einen Quelltext für lilypond generiert [lilyPond].

Da dieses V-Format nur zwei Hakenparameter hat, gibt es auch nur zwei "kontrapunktischen Vertauschungen" von K-Stimme und Hakenparameter. Es bietet sich an, immer beide auch auszuprobieren.
Darüberhinaus gibt es nur 4^2 "horizontale Kombinationen mit Wiederholung" von synchronen Haken gegeneinander, 4*3 von Haken und Konstantwert (aufgeteilt auf zwei Stimmen: 4*3*2) und 12^2 von synchronen Doppelhaken.
Auch diese Kombinationen sind also noch wenig zahlreich und könnten leicht erschöpfend dargestellt werden.

Zunächst verwenden HKN_v00/vox_alle_zweier.haken, HKN_v00/vox_alle_zweier_0.pdf und HKN_v00/vox_alle_zweier_1.pdf die Kombinationen von synchronen Haken gegeneinander, und gegen Konstantwerte. Es erwies sich als gar nicht so einfach, eine "musikalisch"/ästhetisch/rezeptionstechnisch sinnvolle Anordnung zu finden, -- siehe die Dokumentation im Quelltext.

Auch die 12*12=144 Kombinationen von Doppelhaken sind noch durchaus darstellbar. Das wären bei interner Überlappung (6*6+6*5)*12 = 66 * 12 = 792 Anschläge. Damit allerdings nähern wir uns dem Bereich, wo eine programmierte Generierung (/algorithmische oder deklarative Beschreibung) der Hakenfolgen sinnvoller wird, wie oben als Alternative angedeutet, siehe Abschnitt 6.1. Ein solch kataloghaftes Ergebnis scheint kaum noch ästhetisch interessant.

Die folgenden Studien behandeln die Doppelhaken folglich durchaus eingeschränkt, und zwar (a) nur solche mit interner Überlappung, die also in fünf(5) RelWerte expandieren, (b) davon einer in der einen Stimme gegen mehrere in der anderen gesetzt, also nicht mehr synchron sondern augmentiert, und (c) mit bestimmten globalen Symmetrieen und (d) internen Reihen-Eigenschaften (All-Eigenschaften).
Ein erster ausführlich dokumentierter Quelltext ist HKN_v00/vox_fuenf_doppelhaken.haken, die Übersetzungen sind in HKN_v00/vox_fuenf_doppelhaken_0.pdf und HKN_v00/vox_fuenf_doppelhaken_1.pdf.

Darauf baut auf der Kommentartext in HKN_v00/vox_drei_doppelhaken.haken mit den Übersetzungen HKN_v00/vox_drei_doppelhaken_0.pdf und HKN_v00/vox_drei_doppelhaken_1.pdf.

^{^Inh} 7.3 Version "Vla" für Viola Solo

Die Übersetzungen für Viola/Vla haben drei "klassische" Parameter: Tonhöhe, Dauer und Lautstärke. Es werden nur hier mehr als drei Wertstufen im klingenden Vordergrund verwendet, wie oben als Erweiterung beschrieben (Abschnitt 6.5). Dies wird hier realisiert indem für jeden V-Parameter eine oder zwei Stimmen angegeben werden. Falls nur eine(1) Stimme angegeben, dann werden deren Werte verdoppelt und es bleibt bei drei V-Wertstufen. Zwei ausgewählte K-Stimmen werden addiert. Es ergeben sich also Indizes von 0 bis 4 mit folgender Umsetzung:

Dabei ist mit "längstmöglich" ein "langsamer ganzer Bogen" gemeint, was auch für einen evtl. Zuschauer deutlich sichtbar ist, aber bei verschiedener Lautstärke andere physikalische Zeitdauern bedeuten kann.

"höchstmöglich" ist mit den in der Neuen Musik dafür üblichen dreieckigen Notenköpfen notiert.

Die oben in Abbildung Abbildung 21 angegebenen "alternativen Tonhöhen" dürfen vom Solisten improvisierend eingesetzt werden, als Ersatz für Tonhöhen derselben Tonklasse.

Die Implementierung befindet sich in Score_hkn_vla_v00.java (API-Dokumentation), eine abgeleitete Klasse, die (wie oben für Vox) einen Quelltext für lilypond generiert [lilyPond].

Die meisten beigefügten Partituren sind Versionen der generischen Sätze, siehe Abschnitt 7.6.

Dabei sind besonders charakteristisch diejenigen Übersetzungen, die die mögliche erweiterte RelWert-Skala (fünf Werte und zwei K-Stimmen je Hakenparameter) benutzen indem Stimmen der nur dreistimmigen generischen Studien wiederverwendet werden, wie HKN_v00/gen00_vla_132133.pdf, HKN_v00/gen01_vla_132133.pdf und HKN_v00/gen02_vla_132133.pdf.

Es gibt aber auch eine diese erweiterte RelWert-Skala mit dezidierten Stimmen spezifisch behandelnde "Dramatische Introduktion zu einer ganzen Sinfonie", nämlich in Datei HKN_v00/vla_intro_0.haken und HKN_v00/vla_intro_0.pdf.

^{^Inh} 7.4 Version "Sig" für signalerzeugenden Synthesizer

Die Fassungen für Elektronik/Sig haben wieder fast nur "un-klassische" Parameter, Lautstärke und Tonhöhe sind nullgestellt und konstant. Stattdessen gelten

Die Hüllkurve wird direkt in die "physikalischen Sig-Daten" hineingeneriert.

"Hall" wurde auch als weiterer (fünfter) Parameter überlegt, oder aber als Ersatz für einen der anderen.
FIXME es ist noch nicht klar, inwieweit "Hall" überhaupt merklich ist bei Nicht-Vorhandener von sonwohl Klang-Rauhigkeit als auch Hüllkurven-Spitzigkeit.

FIXME MEHR

^{^Inh} 7.5 Version "Svg" für bewegte Graphik

Die Fassungen für Graphik/Svg haben naturgemäßerweise wenig "klassisch musikalische" Parameter. Ihr Inhalt ist eine einzige farbig ausgefüllte geometrische Figur, die auf weißen (oder schwarzem) Hintergrund an verschiedene Bildpositionen springt und in Pausen (oder Teilen von längeren Pausen) unsichtbar bleibt. Obwohl der einzig naheliegende musikalische Parameter, die Dauer, bemerkenswerterweise keiner davon ist, hat diese Version die meisten Hakenparameter. Diese sind:

(Wenn man Dauer hinzunimmt,kommt man auf SECHS Parameter, dann kann man Sig auch noch auf fünf vergrößern !?!? FIXME)

Dies ist der Quelltext der Übersetzung für dieses rein visuelle Vordergrund-Format. (Er ist recht kurz, und das tscore-Framework ist so leistungsfähig, dass mehr Aufwand wirklich nicht nötig ist!-)

Es folgen erste einfache Studien in Quelltext und Realisierung.
(Es empfiehlt sich, diese in verschiedenen "Festern" zu öffnen, um den Quelltext verfolgen zu können!-)

HKN_v00/svg_triangle_0.haken und HKN_v00/svg_triangle_0.svg
und HKN_v00/svg_triangle_1.haken und HKN_v00/svg_triangle_1.svg.

^{^Inh} 7.6 Generische Vorstudien

Kanonische Wanderung aller vier Haken-Modi durch drei Stimmen in HKN_v00/gen00.haken, übersetzt nach HKN_v00/gen00_vla_123.pdf, HKN_v00/gen00_vla_312.pdf, HKN_v00/gen00_vla_221.pdf und HKN_v00/gen00_svg_12123.svg.

Das V-Format "Vla" erlaubt ja zwei K-Stimmen je V-Parameter. Unter Wiederverwendung ergibt sich z.B. HKN_v00/gen00_vla_132133.pdf, das zum ersten Mal mehr als drei Dauern und Tonhöhen zeigt.

Da nicht-auftretende K-Stimmen auch keine K-Ereignisse erzeugen, können umgekehrt die generischen drei-stimmigen Partituren auch in das V-Format "Vox" umgesetzt werden, also mit einer echten Untermenge der K-Stimmen, ohne dass redundante Wiederholungen auftreten, siehe HKN_v00/gen00_vox_12.pdf und HKN_v00/gen00_vox_23.pdf.

Drei verschiedene Hakenreihen, nacheinander in drei Stimmen zeigt HKN_v00/gen01.haken, übersetzt nach HKN_v00/gen01_vla_123.pdf, HKN_v00/gen01_vla_312.pdf, HKN_v00/gen01_vla_221.pdf und HKN_v00/gen01_svg_12123.svg.

Ein eher "dramatisches zunhemendes Ineinanderschieben" von Haken verschiedener Augmentationsstufen zeigt HKN_v00/gen02.haken, übersetzt nach HKN_v00/gen02_vla_123.pdf und HKN_v00/gen02_svg_12123.pdf

^{^Inh} 7.7 Erfahrungsbericht

Die Arbeit am HKN-Projekt und an der Kompositon "HKN_v00" war integrierte Forschung insoweit, als die zunehmende Erkenntnis der ästhetischen Notwendigkeiten ständige Weiterentwicklung der Software verursachte. Diese Notwendigkeiten sind nicht so sehr die Bedürfnisse zur Gestaltung, als vielmehr die spezifischen Eigenschaften des menschliche Rezeptionsvermögens, -- für dessen Lehre ja der Term "Ästhetik" ursprünglich steht.

Dies waren die wohl wichtigsten Einzelschritte:

1. Die eigentlich inhaltliche Kompositionsarbeit wurde begonnen mit der Version "Vox" und "Graphik". Erstere, weil sie nur zwei Parameter kennt; letztere, weil ihre Ergebnisse unmittelbar überprüfbar sind (SVG im Browser).
2. Als erstes fiel auf, wie oben bereits erwähnt, die Notwendigkeit extern gesetzter Pausen.
3. Dann der "Apostroph-Operator": dieser verhindert unbedingt die Überlappung mit dem Ende des vorangehenden Hakens, auch wenn dazu K-Zeitpunkte synthetisiert werden müssen, siehe oben Abschnitt 6.4.
4. Dann dessen Gegenteil, der Bindebogen "~", der die Überlappung mit dem Schluss der vorangehenden Hakens erzwingt, auch wenn sie nicht durch Mangel an K-Zeitpunkten nahegelegt wird. Dies wurde notwendig in der Vox-Stimme, wo "Doppelhaken gegen augmentierte Doppelhaken" stehen sollen, beide mit Auslöschung.
5. Dabei erst wurde auch die Unterstützung von Doppelhaken als eigene Events als notwendig erkannt und relativ spät die Implementierung entsprechend erweitert, s.o. Abschnitt 6.7.
6. Für "expositionelles Verhalten" kann die lineare Anordnung eines Parameters (als Kontrapunkt zu einem Haken) sinnvoll sein. Da diese jedoch eine Ausnahme bleiben soll, wurde dafür absichtlich kein abkürzendes Eingabezeichen implementiert. (Sie ist ja als Folge "U-M-O" oder "O-M-U" in diesen einfachen Satzzusammenhängen jederzeit explizit notierbar.)
7. Eine expressionbasierte Eingabe stellte sich sehr bald als ebenso wünschenswert heraus wie die "achsen-orientierte", "analoge". Beispiele sind die Ausdrücke wie
   (pf;ipf;f;ipf;pf)|if
   ...im Kommentartext von vox_fuenf_doppelhaken.haken . Das Format tscore als soll ja als solches schon irgendwann zukünftig eine möglichst bruchlose Einbettung von Expression- und Achsen-Paradigma erlauben, deshalb wurde hier keine ad-hoc-Lösung weiterverfolgt.
8. Andererseits war sehr erfreulich die Leistungsfähigkeit der tscore-Infrastruktur: die Quelltexte, die die unterschiedlichsten Semantiken realisierten, waren nie sehr lang, siehe die obenstehenden Verlinkungen ab Abschnitt 7.2.
9. Was die Anforderungen an den tscore-Quelltext angeht, so stellten sich sehr früh notwendige Anpassungen heraus:
   1. Die Methode "unifyEventTimesByScalarValue()" musste definiert und angewandt werden, denn sonst werden z.B. 1/2 und 2/4 (innerhalb eines top-level-Abschnittes) nicht als der gleiche Zeitpunkt behandelt.
   2. Die Anforderungen dass auf einem Zeitpunkt der T-Leiste immer ein Event stehen muss, wenn irgendwann danach eines steht (Fehlermeldung "error: events with missing beat event ...") ist für den HKN-Anwendungsfall zu restriktiv. (Aber zur Zeit noch nicht geändert, siehe z.B vox_fuenf_doppelhaken.haken, Takt 10, Mitte.)
10. Ausserdem fanden wir natürlich noch einige kleinere Bugs in der Metric-Split-Infrastruktur.

^{^Inh} 7.8 Nice-to-haves, fehlende Implementierungsdetails

Wegen der begrenzten Kapazität und ungünstigen Kosten-Nutzen-Verhältnisses sind einige Punkte, die sich als durchaus wünschenswert herausgestellt haben, noch nicht implementiert:

1. Zur Zeit muss am Ende jeder Stimme ein "Abschlagsereignis" stehen: nur eine einfache RelWert-Angabe am Ende ermöglicht, dass ein vorangehender Haken auch expandiert wird. Dies kommt wegen des Verhaltens des Algorithmus im Randfall und könnte durch eine Modifikation, die ein "synthetisches Stopp-Ereignis" erste einfügt, dann wieder entfernt, ersetzt werden.
2. Ein zweites Partiturformat, das K-Stimmen und V-Stimmen abschnittsweise und textuell zuordnet (also Eingabedatei, Stimmenname, V-Format, Ausgabedateiname, etc.) scheint sinnvoll. Dies geschieht zur Zeit mit Regeln im Makefile und Kommandozeilenparametern.
3. Auch manche Übersetzungsparameter (z.B. Pausenlänge, etc.) sollten konfigurierbar sein. Dies entweder mit einer eingenen Datenstruktur, oder im Rahmen der entsprechenden "FORMAT"-tscore-Erweiterung.
4. Für die Streicher-Übersetzung ist ein "meta-Parameter" sinnvoll mit U=portato, M=legato, O=glissando = Bewegung über die gesamte Tondauer.
5. Für die Streicher-Übersetzung ist die Dauernfolge U=1/16, M=1/8, O=3/16 sinnvoll, da sie rasante "Walkürenritt-" und "Gigue-"Rhythmen produziert.
6. Es könnten "aggressivere" Verfahren der automatischen Überlappungserkennung sinnvoll sein, siehe Abbildung Abbildung 26:
   (a) Teste die letzten beiden und die ersten beiden eines Hakens auf Gleichheit.
   (b) Lösche einen M-Wert, wenn er linear durchschritten wird, also ersetze O-M-U durch O-U und U-M-O durch U-O
   (c) Kombiniere gar beides, also ersetze O-M am Ende des ersten und O-U am Anfang des folgenden durch O-U.
7. Die generische Partitur HKN_v00/gen00.haken, übersetzt nach HKN_v00/gen00_vox_12.pdf und HKN_v00/gen00_vox_23.pdfverwendet nur eine echte Untermenge der drei H-Stimmen. Bei der Schreibweise in der H-Partitur folgt im V-Resultat immer ein "V-Ereignis (hier immer durch Konstante "M"), wenn in der fehlenden K-Stimme ein ganzer Haken steht. Um dies zu vermeiden wäre ein "End-of-Haken-Ereignis" sinnvoll, was nur das Beenden des letzten Segmentes und Festhalten des letzten Wertes bedeutet, aber von sich aus kein V-Event erzeugt.
8. Für die V-Formate Vox und Vla werden ja jetzt schon lilypond-Ausgaben erzeugt. Diese können leicht im "Midi" Dateien konvertiert werden, und die dann mittels Sample Player etc. klangliche Realisierungen. Diese hier zu präsentieren brächte einen deutlichen Gewinn an Anschaulichkeit.
9. Ebenso ist eine "Jnlp"-Realisierung sinnvoll, die dem Leser erlaubte, selbst mit den Dateien zu spielen.
10. Eine rein graphische Partitur-Ausgabe (ähnlich wie die unter den Notentexten gesetzten Symbole, aber diese deutlicher zur Grundlage machend und nicht nach dem V-Zeitpunkten, sondern ihrer eigenen Abfolge nach anordnend) stellte sich in vielen Fällen als zusätzliche Darstellung der gemeinten Verläufe als wünschenswert heraus. Der Kompositionsprozess verlief häufig "mit Papier und Bleistift" die Hakenkonstellationen malend, bis sie die gewünschten Eigenschaften aufwiesen. Dafür wäre eine solche Übersetzung zweckmäßig. Aber auch zur Ausführung, als "Improvisationsvorschrift" für Musiker.
    Die Realisierung einer solchen rein graphischen Partitur könnte SVG, xfig oder LaTeX basiert sein, oder direkt in Java-Awt erfolgen, oder als Instanz des (zukünftigen!-) mugraph-Frameworks. Dies ist aber noch offen.
11. Ähnlich ein reiner Expandierungslauf, der alle Haken in Folgen von RelWerten auflöst und eine wiederum parsierbare tscore-Eingabe generiert.

^{^Inh} 8 Historisches

Eine eigene Unterdatei bringt die Wiedergabe einiger der damaligen Dokumente, welche auch für diesen neuen Anlauf HKN-v00 durchaus nochmals ausgewertet worden sind. (Verfasser weiß allerdings selbst kaum noch, was sie bedeuten sollen; sie sehen teils aber so hübsch aus, dass sie der Nachwelt überliefert seien :-)

^{^Inh} Bibliographie

made    2022-08-24_11h37   by    lepper   on    linux-q699.site         
produced with eu.bandm.metatools.d2d    and    XSLT