| zu den Gesamtinhaltsverzeichnissen |
| ^inh 2013120500 | phaenomen |
1
Aufgabenstellung
1.1
im Spannungsfeld zwischen Metrik-Mittelgrund und Rhythmus-Notation
1.2
Eigenschaften, Arten und Rollen von Algorithmen
2
Der "metricSplit" Algorithmus zur metrik-adäquaten Notation von
Ereignisfolgen
2.1
Übersicht
2.2
Eingabe: Dauern, Zeitpunkte und Ereignisse
2.3
Der Metrikbaum
2.4
Eingabe und Phase Null/Prop:
Konstruktion von Metrikbäumen durch Metrikbaum-Spezifikationen, Propagierung
der Dauern-Informationen
2.5
Exkurs: Konventionelle Taktart-Bezeichnungen und Metrikbaum
2.6
Verhältnisse von Metrikbaum und zu notierendem Rhythmus
2.7
Eingabe: Stilparameter
2.8
Dauernwerte und Schreibweisen
2.9
Proportionen in der Vordergrund-Notation
2.10
Arten von Proportionen
2.11
Phase Null-Zwei/Prop-Zwei: Vorbereitung der n-olen-Klammern;
Kriterien für Schreibbarkeit
2.12
Phase Eins/IC: Finden der Initialen Überdeckung
2.12.1
Exkurs: Typische Verwendung der Alternativen für die
Festlegung der Scheibweisen von spontanen n-olen
2.13
Phase Zwei/Div: Synthese und Hinzufügung weiterer Teilungen
2.14
Phase Zwei-B/Approx: Approximierung von höherzahligen Nennern
2.15
Phase Drei/Merge: Mustergesteuerte Zusammenfassende Transformation
(Merging Transformations)
2.15.1
Grundsätze
2.15.2
Anwendbarkeit der Muster und E-Schreibbarkeit von Knoten
2.15.3
Verschmelzung von Geschwistern
2.15.4
Verschmelzung mit Cousinen: Synkopen und Hemiolen
2.15.5
Mehrfache Synkopen
2.15.6
Verschmelzung mit Tanten und Neffen: Punktierungen
2.15.7
Exkurs: Die nette, aber problematische Teilung durch vier(4)
2.16
Konflikte bei der Transformation
2.16.1
Konflikt Geschwister vs. Cousinen
2.16.2
Konflikt Geschwister vs. Punktierung
2.16.3
Konflikt Positive vs. negative Punktierung
2.17
Kombinationen von Transformationen:
Zweier-Synkope und Hemiole vs. Punktierung
2.18
Phase Vier/BrSel: Auswahl der notwendigen n-olen-Klammern
2.18.1
Exkurs: Zweckmäßigkeit Verselbständigter n-olen
2.19
Phase Fünf/Nota: Generierung der Notationssymbole, Übergang von
Knoten auf Noten
2.20
Phase Fünf/Nota: Minimale Freie Zerlegung
3
Ausblick
3.1
Mögliche Verwendungen
3.2
Mögliche Erweiterungen
4
Demo-Applikation DemoMetric
5
ANHANG:
Genauere Diskussion von E-Schreibbarkeit und Zusammenfassenden Transformationen,
nebst lustigen extremen Beispielen
5.1
Zusammenfassende Überlegungen
5.2
Beispiele für Kombinationen aus drei(3) und fünf(5)
5.3
Beispiel für Punktierungen und Abkürzende Proportionen
5.4
Beispiele für die höheren Spontanen Ausnahmen
6
Danksagung
Im Vorgängerartikel senza tempo 20121027 00 haben wir ausführlich die Grundlagen und Mittelgrund-Konzepte der mehr oder weniger avancierten Konstruktion von Takt-Metriken im Rahmen der "Common Western Notation", "CWN", diskutiert. Dort war dies u.a. Vorbereitung für Rezensionen von älteren Publikationen zu Problemen der "taktart-konformen Rhythmusnotation" am Schluss des Artikels. Hier nun, wie angekündigt, unser eigener Ansatz.
Zunächst einmal sei definiert, dass eine Metrik die lückenlose Zerlegung der Gesamtdauer eines Taktes in Unterabschnitte darstellt, wobei jedem dieser Abschnitte je unterschiedliche Rollen und Regeln, Spielweisen und Wirkungsmuster zugeordnet werden können. Welche, ist abhängig von Stil, Epochen und Gattung und wird hier nicht behandelt. Fundamental ist aber, dass diese Zerlegung rekursiv weitergeführt wird, und jeder dieser Unterabschnitte auch wieder dieser Art von Zerlegung unterworfen werden kann; es ergibt sich eine metrische Hierarchie.
Ein Musikstück bestehe aus Takten; je Takt gelte eine Metrik.
Ein Rhythmus sei eine Folge von Startzeitpunkten, die in einem Takt notiert werden sollen.
Es müssen nun verschiedene Aufgabenstellungen im Spannungsfeld zwischen taktbasierter Metrik und Rhythmus wohl unterschieden werden, da sie zwar teilweise eng zusammenhängen, teilweise aber auch gar gegensätzliche Voraussetzungen und Konsequenzen mitsichbringen. Es sind ...
Die Induktions-Problem ist fast die gegenteilige Aufgabenstellung zum Notations-Problem; das Abweichungs-Problem muss in praktischen Zusammenhängen durchaus als Erweiterung des Notations-Problems behandelt werden. Dieser Text behandelt nicht das Induktions-Problem.
Das Notations-Problem wurde
im Vorgängerartikel
wie folgt präzisiert:
Es besteht grundsätzlich darin, eine abstrakt gegebene Folge von Ereignis- und
Pausendauern (z.B. codiert als rationale Zahlen), die genau die Dauer
eines gegebenen Taktes (mit einer bekannten metrischen Struktur) füllen, in eine Folge
musikalischer Dauernsymbole zu übersetzen.
"Dauernsymbole" sind dabei im allgemeineren Sinne alle "terminalen Symbole" der
CWN-Notation, welche Dauern ausdrücken, also Formen der Notenköpfe, Fahnen oder
Balken, Verlängerungspunkte, Haltebögen und n-olen-Klammern.
Im engeren Sinne, immer
dann, wenn sie gezählt werden und ihre Anzahl minmiert, gelte ein(1) Notenkopf nebst
seinen Verlängerunspunkten als ein(1) Dauernsymbol.
Zunächst einmal muss diese Notation die Längenverhältnisse der Ereignisse und der Taktdauern korrekt wiedergeben. Dies scheint zwar eine selbstverständliche Forderung, wird aber dennoch im folgenden explizit als "Arithmetische Korrektheit" bezeichnet, und genauere Blicke in die historische Praxis werden sie als durchaus kritisch aufweisen.
Eine viel wichtigere und schwieriger zu fassende Eigenschaft nennen wir "Ergonomische Zweckmäßigkeit". Sie bedeutet, dass die jeweils gewählte Schreibweise die hierarchischen Ebenen innerhalb des Taktes möglichst deutlich zum Ausdruck bringt. Dies unterstützt das korrekte Notenlesen und Musizieren, da in metrischen Kontexten das Zeitgefühl sich viel mehr an diesen Hierarchien orientiert als an der abstrakten "berechneten" Dauer eines Ereignisses.
Als weitere wichtige Eigenschaften sehen wir "Stilistische Angemessenheit" und "Innere Konsistenz". Erstere ist eine historische Kategorie, welche die verlangt dass die in der Praxis entwickelten Konventionen je Gattung, Stil und Epoche auch von einem Algorithmus getroffen werden können; zweite bedeutet, dass gleiche und ähnliche Konstellationen an verschiedenen Stellen des Mittelgrundes auch überall gleich oder ähnlich in eine Vordergrundform übersetzt werden sollten. (Dies wird in unserem Ansatz durch Momente der "dynamischen Programmierung" erreicht, durch "caching" auf den verschiedensten Ebenen der Berechnung.)
Eine mathematische Formulierung von Problem und möglichen Lösungen verfolgt grundsätzlich mehrere durchaus unterschiedliche Ziele, deren Extreme sind
(a) "Automatisierung":
In der Praxis der maschinellen Generierung und
Verarbeitung von musikalischen Strukturen ist es häufig nötig, eine
konventionelle CWN-Notation automatisch zu erzeugen.
(b) "(theoretische) Forschung":
Eine funktionierende mathematische Formulierung erlaubt es allemal, theoretische
Diskussionen auf eine exaktere Grundlage zu stellen.
Bereich (b) läßt sich weiter unterteilen: Die Forschung kann (b1) der Modellierung selber gelten, sie kann (b2) verschiedene konkrete Historische Corpora versuchen, mit dem Algorithmen zu re-synthetisieren, und so deren innere Regeln konkreter bestimmbar zu machen, oder sie kann (b3) das Denken des Musikers versuchen nachzubilden, und enventuell sogar ausgewählte Modelle einer (hier: bezogen auf Metriken und Hierarchien, "Zählen" und Wahrnehmen) experimentellen Überprüfung unterwerfen.
Wir leisten hier lediglich die mathematische Aufstellung des Modelles, welches nur Grundlage des Bereiches (b) ist, aber auch eine funktionsfähige Implementierung (mit wenigen Einschränkungen), die als "Java package" vorliegt und in verschiedenste Programmierkontexte unmittelbar eingebunden werden kann.
Der Bereich (b), die theoretische Forschung, kann auch so differenziert werden, dass Folgearbeiten das Modell anwenden können, indem sie vorgefundenen Gegebenheiten zu re-konstruieren versuchen, und dadurch die dazu notwendigen Parameter ermitteln.
Es ist aber bereits die Erstellung des Algorithmus ein Re-Konstruktionsvorgang, und seine dabei festgestellten Eigenschaften sind Indikatoren für Eigenschaften der psycho-internen Modelle der Musiker durch die Jahrhunderte.
Diese Eigenschaften (siehe auch den Vorgängerartikel) sind u.a. ...
Die allerwichtigste und für ihre Rolle als Forschungsmittel fundamentale Eigenschaft jeder algorithmischen Realisierung ist aber die Explizitheit: Jedes Mensch, das sich mit Musik beschäftigt, hat ein intuitives Vorverständnis, eine aus früher Kindheit kommende Erfahrung im Umgang mit Klaviatur und Noten, Tonhöhen und Rhythmen, etc. Diese Erfahrungsschatz kann aber der Abklärung der Gegebenheiten durchaus hinderlich im Wege stehen, allein schon, weil er deren hohen Wert verdeckt. Algorithmisierung verlangt immer das Explizit-Machen aller Gegebenheiten, das Aussprechen, das Bewußt-Machen.
Wichtig (und für die Leser, die eher aus der musikwissenschaftlichen
Richtung kommen vielleicht etwas ungewohnt, zumindest aber nicht
immer unmittelbar präsent) ist, dass jeder Ansatz wie der hier vertretene,
also jeder "mathematische" Ansatz, ein konstruktiver, positivistischer ist.
Es gelten jederzeit ausschließlich die Regeln und Einschränkungen, die
explizit aufgestellt wurden, und was aus ihnen folgt.
Ja, "reine Mathematik" besteht grundsätzlich aus nicht mehr als
genau derartigen Fragen:
Welche weiteren Einschränkungen folgen aus den zu Beginn aufgestellten expliziten
Grundsätzen. Man sehe z.B. den ganzen Kosmos der
Gruppentheorie, der aus drei allereinfachsten Setzungen entsteht.
Es wird dort z.B. nur gefordert, dass es mindestens ein(>=1) "neutrales
Element" gebe. Es folgt dann aus der Assoziativität, dass es
genau ein(=1) solches gibt.
Die Forderung nach Minimalität bedeutet hier, dass die Forderung nach
"genau einem" neutralen Element nicht (gleichzeitig mit der Assoziativität)
zu den Axiomen genommen werden darf, da sie ja ableitbar ist, also als
Axiom nicht erforderlich.
Diese Minimalität ist eine ästhetische Eigenschaft. Im landläufigen
Wortgebrauch: "durch Schönheit befriedigend", aber auch durchaus im
Kantischen: "die Wahrnehmung betreffend".
Der metricSplit Algorithmus, wie hier implementiert, ist ein Algorithmus zur metrik-adäquaten Notation von Ereignisfolgen, also zur "ergonomisch zweckmäßigen", "stilistisch angemessen", etc., wie oben definiert in Abschnitt 1.1.
Der folgende Text erläutert ihn und folgt seinem Ablauf, -- Darstellungen von notationstechnischen Grundlagen, Datentypen, historischen Gegebenheiten etc. werden immer da eingestreut, wo sie dafür notwendig werden.
Die im Vorgängerartikelrezensierten Algorithmen zu diesem Problembereich erhielten die zu bearbeitenden Dauernfolge bereits als Folgen von Notenwerten codiert, und arbeiteten durch deren sukzessive Zerlegung. Im Gegensatz dazu bearbeitet metricSplit beliebige rationale Zahlen als Startzeitpunkte und Dauern, und zwar durch schrittweise Zusammenfassung. Dies geschieht durch eine Abfolge von durchaus verschiedenen Phasen:
Grundlegend wird in Phase eins die Folge der Startpunkte in eine Liste von Listen von Knoten des Metrikbaumes übersetzt. Diese werden weiter transformiert in den Phasen zwei bis vier. In Phase fünf wird dann von Knotenmengen auf ausgegebene Dauernsymbole übergegangen.
Der zu notierende Ryhthmus wird
übergeben als aufsteigend geordnete Folge von Zeitpunkten relativ zum
Anfang des Taktes.
Als erster Zeitpunkt muss der des Taktanfanges auftreten, als letzer der
des Taktendes.
Alle Zeitpunkte bis auf den letzten werden als Beginn eines
Ereignisses aufgefasst, und als Ende des vorangehenden.
Eine parallellaufende Folge Bool'scher Werte gibt an, ob diese Ereignisse Klänge oder Pausen sind. Wir setzen voraus, dass in dieser Darstellung niemals zwei Pausen direkt aufeinanderfolgen. 1
In allen folgenden Betrachtungen und Formeln gilt, dass Dauern und Zeitpunkte (sowohl von primären musikalischen Ereignissen als auch von organisierenden Begriffen wie "Takt", oder abstrakten Teil-Intervallen eines solchen, etc.) stets als positive rationale Zahlen modelliert werden. Beide Größen haben zunächst keine Beziehung zur physikalischen Zeit, zur "Ausführungs-" oder "Aufführungs-Zeit".
Sie werden im folgenden hingegen explizit den Dauernsymbolen der CWN in ihrer konventionellen Bedeutung gleichgesetzt: Die Dauer, die durch die rationale Zahl "1/4" bestimmt wird, entspricht derjenigen, die durch eine "Viertel-Note" bestimmt wird (solange diese nicht unter einer n-olen-Klammer geschrieben ist. Näheres siehe Abschnitt 2.8).
Ein musikalisches Ereignis ist (a) ein in sich homogenes Klangereignis, das ein zusammenhängendes Zeitintervall ausfüllt, oder (b) eine derartige Pause. Wir sagen: Ein Ereignis "findet an einem Zeitpunkt t statt", wenn sein Zeitintervall an diesem Zeitpunkt t beginnt.
((EXKURS:
Diese Trennung wird als eine scharfe durchaus benötigt; in der Praxis finden sich
allerdings häufig Kombinationsformen: Das Symbol einer Halben-Note, mit einem
Haltebogen an eine folgende auf gleicher Tonhöhe gebunden, ist in diesem
Sinne ein einzige Ereignis, dargestellt als zusammengesetztes Symbol. Wird aber nur
über die Länge der ersten Halben eine crescendo-Gabel gesetzt, so ist die Forderung
nach "Homogenität" verletzt und wir müssen zwei getrennte "Ereignisse"
annehmen (die allerdings gebunden interpretiert werden, was aber für unsere
Fragestellung zweitrangig ist.
Viel deutlicher noch wird da Problem bei dem Symbol einer ganzen Note, über dessen
graphischer Breite hintereinander zwei(2) Gabeln, cresc, dann decresc. stehen. Auch
dies kann in unserem Denken nur als zwei "Ereignisse" modelliert werden.
))
Zweite grundlegende Eingabegröße in den metricSplit-Algorithmus ist eine Baumstruktur, die eine intendierte Hierarchie der metrischen Gliederung innerhalb eines Taktes wiedergibt, genannt Metrikbaum, wie bereits beschrieben und mit ausführlichen Beispielen vorgestellt im o.e. Vorgängerartikel , und wie inzwischen implementiert in bandm.eu.music.entities.MetricTree . (Die Form der Bäume im Vorgängerartikel weicht in wenigen aber wichtigen Details von der hier vorgestellten Implementierung ab!)
Es gilt für die konstruktiven Eigenschaften des Metrikbaumes:
Der Kürze halber sprechen wir im folgenden
kurz von "seinem Intervall" für "das vom Knoten repräsentierte Intervall",
und setzen beide in den meisten Kontexten sprachlich gleich, reden also
von "frühester Knoten" statt "Knoten mit
dem frühesten Startzeitpunkt" und "längsten Knoten" statt "Knoten mit
der längsten Dauer".
"Das Ereignis überdeckt den Knoten" bedeutet "die Geltungsdauer des
Ereignisses überdeckt das vom Knoten repräsentierte Zeitintervall";
"die Knoten folgen unmittelbar aufeinander" heißt "die von den Knoten
repräsentierten Intervalle folgen ...", etc.
Wichtig aus Sicht der Ziele und Prinzipien dieser Modellierung ist das oben definierte Prinzip der Explizitheit, dann nämlich für den Aufbau von Metrikbäumen keine weiteren Beschränkungen als die tatsächlich oben positiv aufgestellten gelten.
Die Kindknoten eines Elterknotens können durchaus verschiedene Dauern und verschiedene
innere Struktur haben. Beides ist in der älteren Anwendung von CWN selten der Fall,
macht aber die Flexibilität unserer Modellierung aus (verglichen
mit den
im Vorgängerartikel rezensierten
Lösungen), und ist für
neuere Entwicklungen wie Avantgarde, Jazz, Elektro, etc., durchaus unverzichtbar.
Die Teilung eines Elterknotens heißt äquidistant, wenn alle Kindknoten
dieselbe Dauer haben. Sie heißt äquimorph, wenn alle Kindknoten
dieselbe Dauer und dieselbe (unendliche!) innere Struktur haben.
Für die reine Anzahl der jeweiligen Kindknoten (unabhängig von deren Länge und Teilung!) gilt folgende Klassifikation:
Äquidistante Teilungen in zwei(2) oder drei(3) nennen wir "nett". Diese Teilungsformen sind die grundlegenden, und machen fast alle Situationen aus. Sie gehen auf die intra-psychische Kategorie der "mentalen Einfachheit" zurück, siehe den Vorgängerartikel.
Die Teilung in fünf(5) heißt "semi-nett". Sie kann u.U., je nach Struktur und Charakter des musikalischen Satzes, auch noch als mental einfach empfunden werden. (Wenn nicht, darf sie nicht angewandt werden, sondern muss durch 2+3 oder 3+2 ersetzt werden.) Notationstechnisch ist sie allerdings wesentlich komplizierter, da die Dauer des Knotens bei äquidistanter Teilung meist nur "zusammengesetzt schreibbar" ist (siehe Abschnitt 2.8).
Die Teilung in sechs(6) ist nicht erlaubt. Sie wird nicht als mental einfach empfunden, sondern allemal entweder als zwei-mal-drei oder drei-mal-zwei oder zwei-plus-vier, etc., empfunden, und muss folglich auch explizit so deklariert werden, da diese Anordnungen psychisch und notationstechnisch durchaus verschieden sind.
Teilungen in vier(4) sind erlaubt und "nett", aber "problematisch". Häufig ist zwei-mal-zwei zu bevorzugen. Das ist fast dasselbe, es ergeben sich aber unterschiedliche Begriffe von Synkope und Punktierung, die durch stilparameterkontrollierte Sonderbehandlung teilweise ausgeglichen werden müssen. Die folgenden Überlegungen gehen davon aus, dass die Teilung durch vier(4) zunächst nicht stattfindet; dies wird ausführlicher begründet in Abschnitt 2.15.7.
Alle anderen Teilungen n>5 heissen "Chopinesque". Bei diesen wird
keine weitere innere metrische Hierarchie angenommen, sondern ein bewußt
"a-metrisches" Verhalten und Rezipieren.
Dies wird modelliert durch einen
flachen Baum mit nur einer Hierarchiestufe, die alle diese n Teilungsknoten
gleichberechtigt aufreiht.
Darin sind alle Dauernwerte erlaubt, werden schlicht
hintereinandergeschrieben und durchgehend bebalkt.
3
So wird in einer typischen
"rechte-Hand-Girlande" in einem Chopinschen Prélude, die als
"Achtel-Dreiundzwanzigstole" notiert ist, niemand Schwerpunkte suchen wollen,
die durch metrische Maßnahmen bestimmt sind, sondern ausschließlich durch "frei
im Raum fließende" Melodik, Motivik, Harmonik, Selbstähnlichkeit, Hochtöne,
Espressivität, etc.
Aber auch eine Teilung durch eine so kleine Zahl wie acht(8) kann genau diesen
Charakter haben, z.B. wenn sie einem 6/8-Takt entgegensteht. Ist hingegen eine
metrische Gliederung doch gemeint, so wäre der Zähler acht(8) als 2*2*2 zu
schreiben, und eine Sieben(7) z.B. als 2+2+3!
Umgekehrt kann auch eine Sechser(6)-Teilung, die als metrische Teilung ja
verboten ist, als Chopinesque durchaus auftreten. Die Chopinesque geteilten
Knoten erscheinen meist nur als temporäre Phänomene oder als
lokale Metriken (besser: "Non-Metriken"). Aber auch auf diese Bereiche
sind große Teile des hier vorgestellten Algorithmus' anwendbar,
da ja die Knoten der oberen Ebene durchaus wieder zweigeteilt werden können, um
z.B. Punktierungen aufzunehmen.
Ein Metrikbaum muss konstruiert werden durch eine Metrikbaum-Spezifikation. Dies ist eine ähnliche Datenstruktur mit nur diesen Unterschieden:
Eine Metrikbaum-Spezifikation kann mit den Parsern oder den Konstruktoren der Implementierung erstellt und danach ausgewertet werden wie folgt:
Eine Metrikbaum-Spezifikation wird in einen Metrikbaum überführt, indem (1) alle Dauerninformationen propagiert werden, (2) daraus die Start- und Endzeitpunkte berechnet, und (3) die implizite Zweiteilung aller Blätter hinzugefügt wird.
Die Propagierung der Dauern geschieht so, dass folgende Regeln so oft angewandt werden bis ein stabiler Zustand erreicht wird:
Dieser Regeln sind aus der Beobachtung der Praxis hervorgegangen und spiegeln das Denken des Musikers auf einfachste Weise. 4 Taucht während dieses Vorganges ein Widerspruch auf, oder weist der stabile Endzustand nicht jedem Knoten eine Dauer zu, so beschreibt diese Metrikbaum-Spezifikation keinen Metrikbaum. Ansonsten werden die Start- und Endzeitpunkte berechnet aus den Summen der Dauern der Vorgängerknoten.
Zur Denotation von Metrikbäumen benutzen wir im folgenden die Syntax, die auch von dem in der Implementierung bereitgestellten Parser erkannt wird. (Diese ist etwas anders als die Syntax im Vorgängerartikel!)
Seien a,b,n kleine ganze Zahlen und T1..Tn Terme dieser Denotation, so beschreibt ...
| a/b | einen Knoten der Dauer a/b (gelesen als rationale Zahl) |
| a/b(T) | einen Knoten der Dauer a/b mit der internen Struktur T |
| T1+..+Tn | einen Knoten mit n Kind-Knoten der angegebenen Strukturen |
| T1|..|Tn | einen Knoten T1 mit den Alternativen T2 bis Tn, in abnehmender Priorität. |
| a*(T) | einen Knoten mit a Kindknoten, alle von der angegebenen Struktur T |
| a | einen Knoten mit a Kindknoten, ohne weitere Angabe |
Die im Vordergrund notierten Taktart-Bezeichnungen haben konventionellerweise Formen wie a/b, -- in Avantgarde und Volksmusik auch wie a+b/c, a/b+c/d, etc.
Diese tragen immer zweifache Bedeutung. Zum ersten geben sie, gelesen als arithmetischer Term und ausgewertet als rationale Zahl, die Dauer des beschriebenen Taktes an. Diese Bedeutung ist exakt und eindeutig und automatisch auswertbar.
Zum zweiten geben sie informelle Hinweise auf die möglicherweise gemeinte innere Strukur des Taktes. Im Vorgängerartikel hatten wir noch versucht, diese zweite Funktion, eingeschränkt auf die Bedeutung der westeuropäisch-klassischen Taktart-Bezeichnungen, systematisch abzuleiten, --- auch angeregt durch die dort rezensierten Arbeiten.
Dies halten wir mittlerweile für wenig fruchtbar und fassen eine Taktart-Bezeichnung im notierten Vordergrund nur noch als "Typenschild" auf, das einer expliziten Definition und Verlinkung auf einen Metrikbaum bedarf.
Die begriffliche Konstruktion hinter jenen mag zwar in wichtige Fällen mit mathematischen Methoden rekonstruierbar sein, und ihre Bedeutung (also der gemeinte Metrikbaum) automatisch erkennbar. In vielen anderen jedoch ist die Beziehung zwischen beiden rein historisch und durch Provenienz gegeben: So könnnte "11/4" im modernen Süd-Serbischen immer ein "4+4+3" sein, hingegen im Albanischen des Mittelalters eindeutig ein "3+3+3+2" bezeichnen, etc,.
Jedwede Formalisierung muss da fruchtlos bleiben. Stattdessen können unterschiedliche Kataloge bereitgestellt werden, die unter derartigen Labels den gemeinten Metrikbaum bequem zur Verfügung stellen.
Für die CWN der klassischen Epoche sähe dieser Katalog ungefähr aus wie ...
2/4 ==> 1/2 4/4 ==> 1/1 oder 1/1(2*(2|3)) oder 1/1(2*2*(2|3)) 3/4 ==> 3/4(3) 6/8 ==> 3/4(2*3) 9/16 ==> 3*3*1/16 //etc. |
(Die beiden ausführlicheren Varianten für 4/4 zeigen die Metrikbaum-Spezifikationen, die für die Notation der Teilung durch drei Vierteltriolen resp. Achteltriolen vorsehen, wie weiter unten genauer beschrieben.)
In diesem Zusammenhang wird nochmals deutlich, dass die Ausdrücke der Form "a/b" in der Denotation für einen Metrikbaum tatsächlich rationale Zahlen bedeuten. Diese geben ausschließlich die Dauer eines Knotens an, und werden nicht als Strukturaussage interpretiert. Der Metrikbaum, der mit "3/4" bezeichnet wird, wird auf nächst-unterer Ebene in zwei(2) Knoten der Dauer 3/8 geteilt. Der traditionellen Taktart-Bezeichnung "3/4" entspricht vielmehr der Metrikbaum "3/4(3)"!
Das oben in Abschnitt 1.1 definierte "Notations-Problem" kann nun wie folgt präzisiert werden:
Es gilt, dass alle zu notierenden Ereignisse nur an den (takt-relativen) Zeitpunkten stattfinden, wo auch Knoten des Metrikbaumes beginnen. Sind solche Knoten nicht vorhanden, werden sie in Phase Zwei/Div synthetisiert. Dies ist das ebenfalls von metricSplit abgedeckte, in Abschnitt 1.1 definierte "Abweichungs-Problem".
Wir sagen "ein Knoten tritt klanglich in Erscheinung", wenn an seinem Startzeitpunkt ein solches Ereignis stattfindet. (Es treten an jedem Ereigniszeitpunkt also immer unendlich viele Knoten klanglich in Erscheinung, da die jeweils ersten Kinder auch an diesem Zeitpunkt beginnen!)
Häufig ist es optimal im Sinne der Aufgabenstellung, wenn ein Ereignis
durch nur ein(1) Dauernsymbol dargestellt wird.
Ist eine Darstellung in einem(1) Symbol nicht sinnvoll, wird die Dauer
durch eine Folge von mehr als einem (>1) Symbol notiert, die untereinander
durch Haltebögen verbunden sind.
Die derart angebundenen Symbole
sollten ebenfalls an Zeitpunkten stehen, an denen Knoten des Metrum-Baumes beginnen.
Denn dadurch wird (im Sinne der Ergonomischen Zweckmäßigkeit)
die gemeinte (und in Nachbartakten vielleicht auch
exprimierte) innere metrische Struktur des Taktes optisch weiter verdeutlicht.
Nur wenn das nicht sinnvoll erscheint, z.B. weil die Anzahl der benötigten Dauernsymbole deutlich höher ausfiele, sollte stattdessen eine freie Zerlegung der zu notierenden Dauer, oder von Teil-Intervallen der Gesamt-Dauer, ausgewählt werden (s.u. Abschnitt 2.20),
Wir sagen ein Knoten tritt notationell in Erscheinung, wenn an seinem Startzeitpunkt ein Notensymbol geschrieben wird, das seiner Dauer entspricht. Ein notationell in Erscheinung tretender Knoten tritt genau dann auch klanglich in Erscheinung, wenn er nicht mit einem Haltebogen an seinen Vorgänger angebunden ist. 5
Bei der oben erwähnten Auswahl aus den unterschiedlichen Notationsmöglichkeiten
(siehe Abschnitt 2.6, Listenpunkt 5) spielen Maßgaben von Epoche, Gattung und Stil,
bis hin zu Personalstil und konzeptuell-semantischen Intentionen
eine Rolle.
Eine generelle Algorithmisierung ist nur annäherungsweise möglich, und nur
sinnvoll, wenn sie durch eine Fülle von Stilparametern angepasst werden kann.
metricSplit sieht zwei verschiedene Aggregate von Stilparametern vor:
Parameters_explicitMode
für Entscheidungen, die sich auf einen
existierenden Metrikbaum beziehen. Davon getrennt
Parameters_automatedMode
für die automatischen Erweiterungen
des vorgegebenen Baumes, wenn für bestimmte Proportionen nötig.
Wird dieser zweite Parameterblock zur Gänze weggelassen ("==null"), dann
ist die automatische Erweiterung damit ausgeschaltet und der Algorithmus wird
partiell.
Die einzelnen Parameter werden im folgenden mit den Schritten des Algorithmus dargestellt, den sie beeinflussen.
Die zur Notation von Rhythmen zur Verfügung stehenden Symbole der CWN, unter denen es ja auszuwählen und zu kombinieren gilt, sind
Die Dauer eines klingenden Ereignisses wird dargestellt entweder durch genau einen(1)
klingenden Summanden, oder durch eine Folge von mehr als einem (>1)
klingenden Summanden, verbunden durch Haltebögen.
Ein klingender Summand ist eine Notengrunddauer zusammen mit beliebig vielen
(incl. null(0)) Verlängerungspunkten und einer Proportion.
Die Dauer eines Pausenereignisses wird dargestellt durch einen(1)
Pausen-Summanden oder eine Folge von solchen.
Ein Pausen-Summand ist eine Pausengrunddauer zusammen mit beliebig vielen
(incl. null(0)) Verlängerungspunkten und einer Proportion.
Die Notengrunddauern und Pausengrunddauern werden gegeben durch
graphische Symbole, die durch die Form der "Köpfe", An- und Abwesenheit eines
"Halses" und die Anzahl der "Fähnchen" oder "Balken" bestimmt sind. Sind keine
Verlängerungspunkte vorhanden und ist die Proportion die neutrale (s.u.), so bestimmen
Notengrunddauer/Pausengrunddauer die notierte Dauer vollständig. Die so
darstellbaren Dauern sind Zweier-Potenzen und bilden die Werte
Dg = {2^n | n<=0}.
(Siehe die Tabelle im
Vorgängerartikel, Abschnitt "Dauern"
.)
Ein hinzutretender Verlängerungspunkt addiert die Hälfte der Dauer dazu,
ein weiterer Punkt dazu noch die Hälfte der Hälfte, etc. Die folglich
(bei neutraler Proportion)
darstellbaren Dauern bilden also die Menge
Dp = {g * (2-2^(-p)) | p>=0 und g aus Dg},
mit p als Anzahl der Verlängerungspunkte. Ausgerechnet ergeben sich Dp zu {1, 3/4,
7/8, 15/16, 31/32, ...} Wir sprechen von den Dauern aus Dp als
"Punktschreibweise", während das Wort "Punktierung" für die unten beschriebene
Zusammenfassende Transformation reserviert wird.
Eine Proportion m/k, wobei m/k eine rationale Zahl ist (also als gekürzter
Bruch geschrieben!), multipliziert die wie beschrieben notierte Dauer mit dieser Zahl
als Faktor.
Die Menge der mit dieser Proportion schreibbaren Dauern ist
D(m/k)= {h * m/k | h aus Dp}.
Die Proportion 1/1 heißt die neutrale, alle anderen merkliche.
Proportionen werden in dem hier verwendeten Mittelgrund-Modell
für jeden Summanden einzeln angegeben.
Dies vereinfacht das interne Rechnen
ganz erheblich und erfüllt die oben als wünschenswert aufgestellten
Prinzipien von Kompositionalität und Lokalität (siehe Abschnitt 1.2),
ermöglicht so u.a das freie Rechnen mit Rationalen Zahlen als
Dauernwerte beim algorithmischen Komponieren.
Ausserdem spielen, anders als im historischen Ursprungskontext,
in zeitgenössischen Anwendungen auch vereinzelte und untervollständige n-olen
eine Rolle (siehe Vorgängerartikel), die so besser darstelbar sind.
(Der notationelle Vordergrund der CWN realisiert Proportionen allerdings anders,
mit n-olen-Klammern, siehe nächsten Abschnitt.)
Die Menge der mit bereits einem(1) derartigen zusammengesetzten Symbol
(aus Grundwert, Verlängerunspunkten und Proportion) schreibbaren Dauern ist nun
De = {d | es gibt m/k, so dass d aus D(m/k)}
Es gilt nun trivialerweise De = Rat. Für jedes a/b aus Rat gilt nämlich a/b in D(a/b), denn a/b = 1*a/b, und 1 ist in Dp. Die Dauer "7/4" könnte also notiert werden als ...
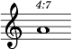
(Diese die Ergonomische Zweckmäßigkeit völlig verfehlende, aber arithmetisch korrekte Möglichkeit ergibt sich nur aus erwähnter Unterstützung verselbständigter n-olen.)
Der Haltebogen erlaubt es nun, eine Folge von mehr als einem
Summanden, soweit bis jetzt konstruiert, zu einer Summe zusammenzufassen.
Die Menge der so schreibbaren Dauern ist nun
Ds = {d1+...+dn| für alle x aus 0..n gilt: dx in De}.
Trivialerweise gilt Ds=Rat, da schon De=Rat gilt, und Rat
bezogen auf die Addition abgeschlossen ist.
Im notationellen Vordergrund
der CWN allerdings werden Proportionen mit n-olen-Klammern notiert.
Diese sind (in der langen, kompositionalen Schreibweise) mit "k:m" beschriftet,
was bedeutet "spiele k Exemplare der Grunddauer X in derselben Zeit, in
der ohne diese n-olen-Klammer m Exemplare gespielt werden würden."
6
(siehe
Vorgängerartikel, Abschnitt über Dauern und n-olen).
N-olen-Klammern überspannen in der historisch ursprünglichen
Anwendung immer eine lückenlose Folge von gleichlangen Notenwerten, mehr als einen.
(Statt jedem von diesen kann ohne Einfluss auf das hier Gesagte
eine arithmetisch korrekte Zerlegung in feinere Werte stehen.)
Man sagt, dass diese Dauern "unter der n-ole stehen".
Es gilt für ihre effektive Dauer ein
auf die notierten Dauern anzuwendender Faktor von m/k;
in unserer Modellierung sind sie entsprechend mit der "Proportion m/k" attributiert.
N-olen Klammern können auch wohlgeschachtelt werden. Die für die darin notierten Dauern gültige Proportion ist das Produkt aller "über ihr" stehenden n-olen. Steht eine Dauer unter gar keiner n-olen-Klammer, so wird ihr die neutrale Proportion 1/1 zugeordnet.
Der für die Arbeitsweise von metricSplit relevante Art einer p = Proportion(a/b) bestimmt sich durch die Größe von a und b ohne den Primfaktor zwei(2). Dieser nämlich läßt sich in CWN jederzeit durch Wechsel des Grundsymboles realisieren, spielt also für Proportion und Schreibbarkeit keine Rolle. 7 Dies vereinfacht die folgenden Überlegungen deutlich.
Sei a'/b' die Proportion, nachdem beide Zahlen durch die maximal enthaltene Zweierpotenz geteilt wurden. Dann gilbt:
Es gelten folgende Zusammenhänge, die auch die Wahl der Namen begründen:
Die Eigenschaft der Notwendigen Proportion (s.o. Abschnitt 2.10, Liste 2, Listenpunkt 2) erlaubt eine effiziente Berechnung der im Ergebnis enthaltenen n-olen-Klammern durch entsprechende Vorbereitung des Metrikbaumes noch unabhängig von jeder konkreten Ereignisfolge:
Für jeden Knoten B des Metrikbaumes, der im Nenner seiner Dauernangabe den Faktor p^n mit n>0 als maximale Potenz von p aufweist, und p!=2, aber sein Elterknoten nur p^x mit 0<=x<n als maximale Potenz, sagen wir, dass B die Potenz "p^(n-x) zwingend (in den Nenner der Proportion) einführt."
Bei der älteren Verwendungsweise von CWN führen alle Kindknoten desselben Elterknotens stets dieselben Potenzen zwingend ein. Alle notierten Symbole im Dauernbereich des Elterknotens werden deshalb i.A. von einer einzigen entsprechenden n-olen-Klammer überspannt, wenn mindestens einer (>=1) der Kindknoten klanglich in Erscheinung tritt. 8
Bei neueren Verwendungsweise ist diese Gemeinsamkeit aber keinesfalls mehr zwingend, siehe das Beispiel im Vorgängerartikel, Abschnitt "Verselbständigte n-olen": --- der zweite Kindknoten der Baumwurzel (Dauer=Triolen-Halbe=1/3) führt den Faktor 3^1 zwingend in den Nenner ein, nicht jedoch der erste!
Die in metricSplit verwendete Datenstruktur vermerkt darum maximale Folgen von Geschwistern, welche dieselbe Proportion zwingend einführen. Man beachte, dass jeder Knoten nur maximal eine(1) Proportion einführen kann, also eine Erkennung von Teil-Überlappungen und Faktor-Zerlegungen (wie "1/3--1/3--1/15" oder gar "1/3--1/15--1/5") nicht stattfindet. Um ein Herausziehen gemeinsamer Faktoren zu erreichen, muss die Metrikbaum-Spezifikation schlicht die entsprechende Hierarchisierung explizit einführen, was der gemeinten metrischen Struktur ja wohl auch adäquater wäre.
Die so erkannten Folgen von Geschwisterknoten sind das Urbild der später im Vordergrund-Notat gesetzten n-olen-Klammern. Ist ein Baumknoten unter diesen ohne Haltebögen schreibbar, also mit nur *e*inem Dauernsymbol, so heißt er e-schreibbar.
Aus beschriebenem Vorgehen folgen wichtige Eingeschaften für die weitere Arbeit von metricSplit:
Der erste Schritt des Algorithmus für eine gegebene Folge von takt-relativen Startzeitpunkten besteht nun in der Konstruktion der Initialen Überdeckung (= Initial Coverage = IC).
Diese ordnet jedem Intervall zwischen zwei benachbarten Zeitpunkten (auch "Ereignis" genannt) diejenige Menge aus dem Knotenbaum zu, welche das Intervall genau überdeckt und minimal ist.
Dies geschieht wie folgt:
Im Falle von best_fit_not_first_fit=true ist die optimale Alternative diejenige, die am wenigsten zusätzlich synthetisierter Proportionen bedarf, dann (nachgeordnetes Kriterium) möglichst wenig Knoten beinhaltet und (schwächstes Kriterium) in der Benutzerdefinition früher steht.
Man beachte, dass die Synthese von notwendigen neuen Unterteilungen in Phase Zwei/Div erst an den Blättern des MTS beginnt, also erst unterhalb der kleinsten vom Benutzer explizit angegebenen Teilungsebenen. Bei einer MTS = 4/4(2*2) also erst ab der Viertelnote. Will man gröbere Zusammenfassungen, so kann man sie allemal explizit als Alternativen angeben, wie in 4/4(2*2|3).
Im folgenden Beispiel ist die IC gesucht für ein Ereignis, welches mit dem Startzeitpunkt von Knoten 12 beginnt und mit dem von 33 endet. Es ergibt sich als IC die Knotenmenge {12, 13, 22, 31, 32}, und zwar unabhängig von jeder internen Struktur von 22:
p
/ | \
21 22 23
/ | \ /|\ / | \
/ | \ / | \
11 12 13 31 32 33
| |
[---------------]|
|
In ein Vordergrund-Notat übersetzt ergäbe dieses fünf mit Haltebögen aufaddierte Notenwerte, die den vom Ereignis überdeckten Knoten des Metrikbaumes unmittelbar entsprechen.

Diese Darstellung ist zweifellos arithmetisch korrekt, aber nicht ergonomisch zweckmäßig im Sinne der Aufgabenstellung. Deshalb erfolgen als naheliegende nächster Schritt die in Abschnitt 2.15 beschriebenen Zusammenfassenden Transformationen dieser Knotenmenge, kontrolliert durch die Gestalt des Metrikbaumes,
Die wichtigste Rolle des Alternativ-Operators (in der eher
historisch-konventionellen Verwendung von CWN) ist es, die von der
normalen Teilung im Metrikbaum abweichenden, "spontanen" n-olen
vorzubereiten und ihre Klammerung festzulegen,
wie zu Beginn definiert als "Abweichungs-Problem" (s. Abschnitt 1.1,
--- Diese Praxis ist geerbt von den Vorläufern der CWN,
die in Form von "lokalen Proportionen" oder
"Kolorierungen" solches in einigen "manirierten" Epochen exzessiv betrieben hatten.)
Immer dann ist zwecks adäquater Notation ein neues, lokales Metrum
im Sinne Anfangs aufgestellter Definition nötig.
Generell gilt: Das Induktions-Problem (=vollständigen Synthetisierung eines Metrums) nur aus einer Folge von Dauernwerten ist nicht eindeutig lösbar.
Dies ergibt sich schon aus der einfachen Tatsache, dass ein Metrikbaum
einen weitergehenden Informationsgehalt hat als eine schlichte Folge von Dauern,
siehe z.B. die naheliegendsten der aus der Folge von reinen Dauernwerten
3/8 1/8 1/8 1/8
synthetisierbaren Metren:

Die Alternative ist eine vollautomatische lokale Modifikation eines vorgegebenen Metrums, wie in der Phase Div von metricSplit ja durchaus realisiert. Aber auch diese Methode ist nicht ausreichend, aus folgender Überlegung:
Rein arithmetisch korrekt sind nämlich alle Dauern immer dann notierbar, wenn die im Nenner auftretenden Faktoren irgendwo in einer n-olen-Klammer über der Dauer auftreten. Man kann also brute-force das "Kgv" aller auftretenden Nenner als eine große n-olen-Klammer über den ganzen Takt setzen, und alles wird notierbar: für alle Dauern, die diesen Divisor nicht benötigen, kann dieser ja kompensiert werden kann, siehe Abschnitt 2.10, Liste 2, Listenpunkt 4. (Am einfachsten geht das noch mit Verlängerungspunkten für die Faktoren (2^n)-1, also 3, 7, 15, etc.)
Genauso aber können aber die zur Notation einer bestimmten Dauer notwendigen Faktoren in ihrem Nenner auf jeder beliebigen Teilungsebene gesetzt werden, mit demselben mathematischen Ergebnis. Soll z.B. das Schmiede-Motiv aus dem Ring in ein schlichtes 3*1/4-Metrum eingeschrieben werden, so müssen Triolen eingeführt werden, was laut obiger Ausführung auf den verschiedensten Ebenen möglich ist. Folgende Schreibweisen sind rein arithmetisch alle korrekt, aber offensichtlich nicht alle ergonomisch zweckmäßig:

Welche von diesen Varianten überhaupt sinnvoll und angemessen sind, kann ein völlig eigenständig operierender Algorithmus nicht beurteilen. Wir sehen hier z.Zt. noch keine Chance für eine sinnvolle Heuristik. (Das einzige offensichtliche objektive Kriterium ist, dass Variante SM-84 einen Knoten mehr enthält, da dort eine schwere Zeit klanglich nicht erscheint.)
Dies zeigt deutlich, dass die möglichen alternativen Metren
(in den meisten Fällen) explizit angegebbar sein müssen, um
genau die dort auftretenden Effekte steuerbar zu machen.
Obige Ergebnisse werden dann durch die Alternativen in folgenden
Metrikbäumen zwangsläufig hervorgebracht:
SM-48 von 3/4(3|6+3)
SM-84 von 3/4(3|3+6)
SM-888 von 3*(1/4|3)
9
SM-16 von 3*2*(1/8(2|3))
Dennoch aber kann "best fit" mit der oben genannten Bewertungsfunktion
durchaus sinnvoll sein.
Die Formel
(1/4|3)+((1/4|3)(1/4|3)|3)
erlaubt sowohl überall Achtel-Triolen, aber auch eine Viertel-Triole
auf den letzten beiden Zählzeiten.
Die Dauernfolge
1/8 1/24 1/12 1/6 1/6 1/6
wird übersetzt in

Da die Variante mit der Viertel-Triole in der Metrikbaum-Spezifikation hinter der mit den drei Achtel-Triolen steht (=geringere Priorität), würde ein first-fit-Verfahren die Zeile SM'888 auswählen. Das best-fit aber erkennt die geringere Knotenzahl von SM'84.
Das Finden einer IC beinhaltet, falls durch Stilparameter erlaubt, die Synthese neuer alternativer Unterbäume für sonst nicht darstellbare Faktoren im Nenner der Eingangszeitpunkte, siehe Abschnitt 2.12, Listenpunkt 4, Listenpunkt 5, Listenpunkt 2.
Dies ermöglicht praktischerweise Kompositionsalgorithmen zu programmieren, die intern mit beliebigen Rationalen Zahlen rechnen und deren Ausgabe immer visualisierbar ist. Selbst wenn "krumme" Werte auf Rechenfehlern basieren und nicht intendiert sind, ist doch gerade dann eine derart vollständige Visualisierung ein wertvolles Werkzeug zur Programmentwicklung.
Hier nun beginnt ein Bereich, der im Sinne oben aufgestellter Unterscheidungen
(siehe Abschnitt 1.2) nicht mehr systematisch sondern heuristisch
gelöst wird: Es werden bestimmte Konstellationen von neuen Divisoren
betrachtet, die in der Praxis häufig auftreten.
Unterhalb dieses Bereiches aber muss zwangsläufigerweise wieder ein
"systematischer" folgen, um die Totalität des Algorithmus' zu gewährleisten,
also die Fälle zu behandeln, die nicht zu den heuristisch behandelten gehören.
Grundlage der Berechung ist, wie dem Algorithmus Abschnitt 2.12, Listenpunkt 4, Listenpunkt 5, Listenpunkt 2 zu entnehmen, immer ein "Blatt" der Metrikbaum-Spezifikation, also ein Knoten ohne explizite Kinder. Diese erhalten also hier eine weitere semantische Bedeutung, über die Aufspannung des unendlichen Metrikbaumes hinaus. Heiße dieser im folgenden "Blattknoten".
Es werden, wie oben bereits erwähnt,
alle Zeitpunkte aufgesammelt, die in die Dauer des Blattknotens fallen.
(Für den Rest des Textabschnittes kurz "gesammelte Zeitpunkte" genannt.)
Die Anzahl dieser ist mindestens einer (>=1).
Aus den gesammelten Zeitpunkte werden
die Notwendigen Proportionen synthetisiert, und die notwendigen
neuen n-olen-Klammern letztlich der Dauer des Blattes eingeschrieben.
Folglich liegen diese immer auf relativ kurzen Grundwerten, und fassen auch
keine expliziten Knoten jemals zusammen:
Ein als 4/4(4) spezifizierter
Takt mit je einer Sechzehntel-Septole in zwei verschiedenen Vierteln
wird über diese beiden je eine eigene Septolenklammer erhalten, auch bei
adjazenten.
Es ist auch keineswegs angestrebt, ja vielleicht sogar unmöglich, dass die synthetisierten Notate in jedem Falle stets ästhetisch und ergonomisch befriedigend sind. Der Benutzer hat ja jederzeit die Möglichkeit, auf die Mehode der expliziten Alternativen zurückzugreifen, wie beschrieben in Abschnitt 2.12.1, und das Metrum als 4/4(4|7) oder als 2*2(1/2|7) zu definieren, resultierend in entsprechend weiter-gefasste Klammern im Notat. Es werden, wie erwähnt, auch keine n-olen oberhalb der Blätter des MTS generiert; sind solche gewünscht, so müssen auch sie explizit vorbereitet werden.
Das hier sämtliche in den Blattknoten fallenden Ereignisse gemeinsam berücksichtigt werden, bedeutet einen deutlichen Paradigmenwechsel: Der Algorithmus wird von einem lokalen (der immer nur einen(1) Zeitpunkt zu betrachten brauchte) zu einem kontext-sensitiven (vgl. Abschnitt 1.2).
Als erstes wird immer ein "neuer Knoten" erzeugt, der später, falls diese Variante sich im übergeordneten Suchvorgang sich letztlich durchsetzt, als neue Alternative hinten an die Alternativen des Blattknotens angehängt wird.
Gundlage der Berechung ist für jeden Zeitpunkt der "relative Zeitpunkt", der Abstand zum Beginn des Blattknotens, und der "fehlende Faktor", d.i. der Faktor im Nenner dieses relativen Abstandes, der mit den Proportionen im bisherigen Metrikbaum nicht darstellbar ist und die Synthese einer neuen Proportion erfordert.
Es bedeute "Generieren eines Baumes mit dem Faktor f unter dem Knoten k" das Hinzufügen von f äquidistanten Kindern zu k (nebst dem Hinzufügen der Proportion "1/k" in die Hilfs-Datenstruktur des Baumes, wie für den Originalbaum geschehen in Abschnitt 2.11).
Dann gibt es folgende Möglichkeiten:
Das o.e. Zerlegen des Faktors f in eine Proportionen-Hierarchie wird von Stilparametern gesteuert: wenn f=15 und prefer_one_bracket_15_to_16, dann wird eine einzige(1) 15:16 Klammer generiert, statt zu zerlegen. Genauso für f=9 und prefer_one_bracket_9_to_8. Ansonsten wird für jeden Primfaktor von f eine eigene Klammer erzeugt, und bei finer_division_down_not_up==true der numerisch kleinste Divisor nach oben gelegt (also Triole über Quintolen über Septolen, etc.), sonst umgekehrt.
In jedem Falle wird nach der Modifikation des neuen Knotens in
die Ausführung der Phase Eins/IC zurückgesprungen, mit genau denselben
Werten, aber mit dem neuen Knoten als aktuellen Knoten.
Wenn durch die stattgehabte
Knoteneinfügung noch nicht alle Divisoren realsiert worden sind,
hat das zur Folge, dass erneut in diesen Algorithmus hineingelaufen wird,
dann aber mit einfacheren Faktoren.
Der rekursive Aufruf ist also "streng konsumptiv" und wird terminieren.
Die folgenden Beispiele beziehen sich alle auf die aller-einfachste Metrum-Spezifikatioin 1/1. Es sind im einzelnen, jeweils in tscore_Notation und/oder als Dauernfolge:
Synt-1: Fall 1: Nur ein einziger Faktor (4/15 und 11/15)
finer_division_down_not_up = true
T 1 2
VOX M "1/1"
VOX sop ckl (- e -) - (- - a) -
= [0, 4/15, 11/15, 1]
Synt-2: dto, aber finer_division_down_not_up = false
Synt-3: Fall 2: in beiden Dauern-Hälften disjunkte Faktoren
T 1 2
VOX sop (ckl d e) f g a (h c d e f g a)
= [0, 1/15, 2/15, 1/5, 2/5, 3/5, 4/5, 29/35, 6/7, 31/35, 32/35, 33/35, 34/35, 1]
Synt-4: Fall 3: zwei Faktoren, einer enthält den anderen
T 1 2
VOX sop ckl (d e -) - (- - a) -
= [0, 1/5, 4/15, 11/15, 1]
Synt-5: dto
T 1 2
VOX sop ckl (d e -) (- - a)
= [0, 1/3, 4/9, 8/9, 1]
Synt-6: Fall 4: Drei Faktoren, ein gemeinsamer
T 1 2
VOX sop ckl (d e -) g (- - a - - - - ) -
= [0, 1/5, 4/15, 23/35, 1]
Synt-7: Fall 5: An den extremen Rändern nur ein bestimmter Faktor:
T 1 2
VOX sop (ckl d e) (f g a h c)(d e f g a) (h c d)
= [0, 1/12, 1/6, 1/4, 3/10, 7/20, 2/5, 9/20, 1/2, 11/20, 3/5, 13/20, 7/10,
3/4, 5/6, 11/12, 1]
Synt-7b: dito, aber ein Metrum zu "1/1(4)"
Synt-8:
T 1 2
VOX sop (ckl) - - - - (d e - - - - -)
= [0, 5/6, 6/7, 1]
Synt-8b: dito, aber mit "Parameters_automatedMode.recursive_separation==true"
|

Beispiel Synth-7 zeigt, dass diese Heuristik noch nicht alle Fälle löst. Hier wäre "spekulatives wiederholtes Zweiteilen" besser, oder eine Weiterentwicklung der spektralen Analyse. Für viele Fälle aber reichen die momentanen Ergebnisse in der Praxis aber schon aus, wie ja Beispiel Synth-7b zeigt.
[[Dies ist zur Zeit noch nicht implementiert.]]
Diese Phase dient als Alternative zu Phase Zwei/Div.
In ihr werden höherzahlige und im Metrikbaum nicht vorhandene Teilungen
nicht verbatim eingeführt, sondern ein fester Teilungsdivisor so lange
angewendet, bis die entstehenden Teilungspunkte hinreichend nahe an
dem exakten Wert sind, um als Approximation zurückgeliefert zu werden.
Dieses Vorgehen entspricht dem, was digitale Sequencer im Verborgenen
ausführen müssen, hier aber auf die Ebene der bewußten Notation gehoben.
Die steuernden Stilparamater sind zusammengefasst in Parameters_approximationMode . Es sind
Man beachte, dass das unscheinbare allow_coincidence einen Paradigmenwechsel verursacht, zwischen lokal und kontext-sensitiv, im Sinne oben definierter Eigenschaften, siehe Abschnitt 1.2.
Zu Beginn der Phase Drei/Merge ist die Folge der Einsatzzeitpunkte übersetzt in die Initiale Überdeckung, eine Folge von Knotenmengen. Der Startpunkt jeweils des ersten dieser Mengen (in Baumordnung) entspricht dem Einsatzzeitpunkt, die Knoten überdecken das Ereignis, und ihre Anzahl ist minimal.
Hier zeigt sich deutlich die wichtige Eigenschaft der Kompositionalität, vgl. Abschnitt 1.2: Alle Unterbäume werden im folgenden gleich behandelt, egal ob sie aus dem Eingabedatum Metrikbaum-Spezifikation hervorgegangen sind, oder aus der Automatischen Ergänzung in Phase Zwei/Div.
Die Knotenmenge kann jetzt schon direkt in eine Vordergrund-Notation übersetzt werden, indem die Dauern der Knoten notiert werden (diese sind immer schreibbar, wenn auch nicht unbedingt e-schreibbar), wobei alle die zum selben Ereignis/Startzeitpunkt gehören durch Haltebögen verbunden werden, siehe das Beispiel am Ende von Abschnitt 2.12.
Diese Schreibweise ist aber ergonomisch nicht optimal.
Es werden deshalb in Phase Drei/Merge
mustergesteuerte Zusammenfassende Transformationen (Merging Transformations)
angewandt.
Diese sollen in der sich ergebenden Vordergrund-Notation mehrere Knoten der Initialen
Überdeckung statt durch eine Folge von mehreren(>1) mit Haltebögen verbundenen
Dauernsymbolen durch nur ein(1) einziges Notenzeichen darstellen. Die verschiedenen
aus ihnen resultierenden Gestalten (im Mittelgrund des Metrikbaumes und im
Vordergrund des resultierenden Notates) heißen Synkopen, Hemiolen,
Punktierungen und zusammengefasste Geschwister.
Diese entlasten nicht nur das Notenbild durch die geringere Anzahl benötigter Symbole, sondern stehen (in fast allen Anwendungsfällen) auch für historisch definierte, feststehende Muster, die dem Interpreten auf einen Blick wichtige Hinweise auf die intendierte rhythmische Gestalt, Agogik, Ausdruck, etc. geben können. Nicht jede beliebige Zusammenfassung ist also anzuwenden, sondern nur solche, die im Sinne der Ergonomischen Zweckmäßigkeit die Metrik-Struktur des Taktes verdeutlichen.
Die Transformationen zerfallen in zwei Arten:
Geschlossene Muster stellen Minimal- und Maximal-Bedingungen für die Begrenzungspunkte des Ereignisses auf, und auf die Ersatz-Note kann an keine weitere angebunden werden.
Offene Muster stellen nur Minimal-Bedingungen für die Begrenzungspunkte des Ereignisses auf, und an beide Seiten der Ersatz-Note können durchaus weitere Noten angebunden werden.
Die einzelnen Transformationen werden in den folgenden Abschnitten detailliert diskutiert und an Beispielen vorgestellt. Zunächst, in aller Kürze, ergeben sich die Transformationen durch bestimmte "Verwandschaftsverhältnisse" der Knoten im Metrikbaum, und ggfls. zusätzlicher einfacher Bedingungen über deren Teilung und Dauern:
Grundsätzlich wird bei jedem Testschritt auch geprüft, ob die Grenze einer bereits in den Baum eingetragenen notwendigen n-olen-Klammer durch die Zusammenfassung überschritten wird. Dies ist nur erlaubt wenn der Stilparameter merge_may_cross_bracket_limit==true. (Lilypond z.B. kann eine "in der Luft hängende" n-olen Klammer nicht sinnvoll darstellen, also eine, die "in der Mitte" der Ersatznote einer Synkope etc. beginnt.)
Technisch werden die Transformationen einfach dadurch realisiert, dass die Untermenge der Knoten aus der Initialen Überdeckung konstruiert wird, die am Ende tatsächlich notationell in Erscheinung treten sollen. Diesen wird bei der letztlichen Ausgabe die Summe der Dauern aller nicht-erscheinenden Nachfolgeknoten, bis zum nächsten erscheinenden, zugeschlagen.
Allerdings ist die Anwendbarkeit der Zusammenfassenden Transformationen
nicht nur von der abstrakten Form des Baumes
abhängig, sondern auch von der konkreten Schreibbarkeit der beteiligten Dauern.
Die Anwendung einer Zusammenfassung soll ja eine Vereinfachung
des Notenbildes erreichen.
Nun kann es aber sein, dass sich als zu notierende Gesamtdauer der zusammengefassten
Knoten eine solche ergibt, die nicht e-schreibbar ist.
(E-schreibbar sind an dieser Stelle alle Dauern, deren Zähler die
Form (2^n)-1 hat, s.o. Abschnitt 2.11, Listenpunkt 2.)
Diese Gesamtdauer müsste also ganz am Ende des metricSplit-Algorithmus zu
Zwecke der Visualisierung wieder zerlegt werden. Es würde also nur die eine
zusammengesetzte Schreibweise (die der Initialen Überdeckung) durch eine andere
zusammengesetzte ersetzt, die vielleicht sogar von der Struktur des Metrikbaumes
weiter entfernt ist. Dies wäre der Ergonomischen Zweckmäßigkeit ab- statt
zuträglich.
Allerdings kann das Problem der Schreibbarkeit bereits bei der Initialen Überdeckung selbst auftreten, ganz ohne Anwendung einer Transformation: da es keinerlei Einschränkungen über die Dauern der Knoten einer Metrikbaum-Spezifikation gibt, bis auf die der inneren Konsistenz, ist eine solche nicht immer e-schreibbar. Es gibt auch seltene gegenteilige Fälle, in der eine Knotenfolge durch eine Transformation erst e-schreibbar wird (3 mal 5/16-Knoten, s.u. Abschnitt 5.2)
Die folgenden Regeln für die Zusammenfassenden Transformationen beziehen sich also zunächst auf die "abstrakte" Gestalt des Graphen, wie er durch die Knoten einer Initialen Überdeckung herausgeschnitten wird, danna ber auch auf die "konkreten" Dauern, um die Transformationen zu modifizieren oder gar ganz zu unterlassen.
Entsprechend der Aufgabenstellung beziehen sich in den folgenden Unterabschnitten alle Aussagen über "Knoten" und "Knotenmengen" immer nur auf zum selben Ereignis gehörige Knoten.
Es können aufeinanderfolgende Kindknoten desselben Elterknotens
evtl. zusammengefasst werden. Dies nennen wir "Verschmelzung von Geschwistern". Sie
ist möglich innerhalb von Teilungen durch drei(3) bis fünf(5), sowie in allen
Chopinesquen, also auch höherzahligen.
(Die Teilungen durch vier(4) werden wegen ihrer speziellen Probleme weiter unten
nochmals genauer betrachtet, Abschnitt 2.15.7. In Teilungen durch zwei(2) können
die Geschwister nicht verschmelzen, denn wenn beide überdeckt sind, ist es ja auch
der gesamte Elterknoten, und die Kinder treten in der Initialen Überdeckung garnicht
erst auf !-)
Notwendige Bedingungen sind (a) dass die zusammenzufassenden Geschwisterknoten gleiche Dauer haben, und (b) die resultierende Dauer e-schreibbar ist. Nicht notwendig ist, dass die innere Struktur der zu vereinigenden Knoten identisch ist, da diese eh nicht in Erscheinung tritt (weder notationell noch klanglich, siehe folgendes Beispiel, Zeile G1&G2, Takt 4)
Ist die Dauer der Einzelknoten e-schreibbar, genau dann sind es auch die
Zusammenfassung von zweien(2) oder vieren(4). Bei Unterknoten einer Drei(3)teilung
wird durch die Geschwister-Verschmelzung nie eine Veränderung des Problems der
E-Schreibbarkeit eingeführt.
Anders bei drei(3) Geschwistern (möglich ab der Vier(4)teilung): diese können u.U. nicht
vollständig ersetzt werden, siehe Zeilen G3&G4: Die Einzelknoten sind e-schreibbar
(Zähler=3), der zusammengefasste nicht (Zähler=9).

Man sieht dass dieses Muster für klingende Ereignisse wie für Pausen gleichermaßen anwendbar ist. Die Anzahl der erlaubten Verlängerunspunkte wird für klingende Ereignisse begrenzt durch den Stilparameter max_dots_positive, für Pausen durch diesen, und zusätzlich durch Stilparameter max_dots_for_pauses. Werden zuviele Punkte benötigt, dann wird die Transformation nicht angewendet.
Sollen drei(3) oder fünf(4) Geschwister verschmolzen werden, aber nur die Kindknoten sind e-schreibbar, nicht das Ergebnis, dann werden alle bis auf den letzten verschmolzen und dieser angebunden.
Dieses Muster ist ein offenes, es können nach dem letzten Geschwister
im selben Takt noch kürzere "Nichten" angebunden werden, oder Geschwister
anderer Dauer, auch evtl. zusammengefasst, oder im nächsten Takt Beliebiges (Zeile 5b).
Gleiches gilt für vorne angebundenen Dauernwerte (Zeile 5b, letzter Takt).
Mögliches Argument gegen seine ungehemmte Anwendung kann sein,
dass dadurch eine spätere Anwendung des Punktierungs-Musters
verunmöglicht wird, die aber besser wäre im Sinne der Ergonomischen Zweckmäßigkeit
(Zeilen 5c und 5d).
Dies wird weiter unten diskutiert, siehe Abschnitt 2.16.

Die entsprechenden Bäume und Überdeckungen sehen ungefähr aus wie ...
p
//|\ \
/ / | \ \
/ / | \ \
[=========] / \
oder [========]-] |
oder [===========]-] |
oder [==============]-----] ....
|
Dabei steht === für die Geschwister, und --- für Angebundenes. Man beachte dass Zeile 5d von metricSplit nur dann erzeugt wird, wenn die Metrik als (2*2/4)+1/4 o.ae. definiert ist: mehrfache Synkopen überwinden nur Zwei(2)-Teilungen.
Synkopen sind nur möglich bei den Teilungen durch zwei(2) bis fünf(5). 10 Sei E der Elterknoten des ersten Knotens, der zu dem Ereignis e gehört. Beginnt e später als E, hat aber dieselbe Dauer d wie E, dann wird eine Synkope konstruiert und eine einzige Note der Dauer d geschrieben. Dies setzt voraus, dass (a) es sich um ein klingendes Ereignis handelt, nicht um eine Pause 11 , und (b) dass Dauer d e-schreibbar ist.
Synkopen sind also ein geschlossenes Muster: ist das darzustellende Ereignis länger, würden also (vorne oder hinten) noch weitere Notenwerte angebunden, wird die Synkope nicht angewandt. Ihre wichtigste Funktion im Dienste der Ergonomischen Zweckmäßigkeit ist es nämlich, anzuzeigen, dass das Folge-Ereignis am selben Unterteilungs-Punkt beginnt wie dieses hier, also mit "demselben feeling relativ zum Beat" zu positionieren ist, was dann ja nicht mehr der Fall ist.
Darüber hinaus findet eine Synkopen-Notation nur statt, wenn (c) Elterknoten und Nachfolger auf ihrer obersten Gliederungsebene gleichartig geteilt werden. In einem 2*1/4 + 3*1/4-Metrum würde folglich keine Halbe-Synkope auf Zählzeit zwei gesetzt werden. Das wäre rein mathematisch zwar möglich, würde aber das Metrum und den Metrum-Wechsel durchaus verunklaren statt verdeutlichen, und stünde also im Gegensatz zur Ergonomischen Zweckmäßigkeit.
Im Falle des "Bruckner-Rhythmus" als Metrum, also im Falle von 2*1/4 + 3*1/6, wäre eine solche sogar mathematisch fragwürdig: Eine gleichsam "gefleckte" Halbe, die aus einer Viertel und einer Triolen-Viertel zusammengesetzt wäre!
Zusätzlich (d) müssen Synkopen durch Stilparameter eingeschaltet werden:
Sind die Elterknoten zwei(2)geteilt, so muss max_level_syncope_2>=1 gelten.
Sind die Elterknoten drei(2)geteilt, so werden die auf Zählzeit
"Zwei" beginnenden Synkopen mit syncope_2_3==true erlaubt,
die auf "Drei" beginnenden Synkopen mit syncope_3_3==true.
Selbst bei einer fünfer(5)-Teilung kann eine Synkope angewandt werden, wenn die Zähler der Kindknoten Kinder nur durch 3 (und 2^n) teilbar ist, s.u. Abschnitt 5.2. Diese werden mit Stilparameter syncope_longer_4==true eingeschaltet.
Es werden für jede der erwähnten Situationen ein je eigener Stilparameter definiert, da sie durchaus verschiedenen Notationsstilen angehören und sehr unterschiedliche Konsequenzen haben können.
Bei einer Dreier(3)-Teilung können Synkopen, wie definiert, aus systematischer Sicht durchaus auftreten, sind aber konventionellerweise recht ungewöhnlich. Viel häufiger wird ein Ereignis beginnend auf der dritten Position des ersten Elternknotens und endend auf der zweiten Position des zweiten durch eine einzige Note dargestellt. Dies ist eine Hemiole, wie die Synkope ein geschlossenes Muster, und wird durch Stilparameter hemiola==true erlaubt.
Die benötigte E-Schreibbarkeit der Dauer d des Elternknotens ist (wegen dem Faktor zwei(2)) bei Zweier-Synkope und Hemiole identisch mit der der Kindknoten. Beim Faktor drei(3) der Dreier-Synkopen besteht, wie oben ausgeführt, keine so einfache Beziehung.
Die beteiligten Bäume sehen aus wie ...
pp pp
/ \ / \
/ \ / \
p p2 p p2
/ | \ / | \ / \ / \
/ | \ / | \ / \ / \
Hemiole [----]| | |
Synkope [---------]| | [--------]|
oder [----------]| |
|
Synkopen werden i.A. nicht von der Teilung des Großelter-Knotens bedingt, und können mehrfach hintereinander angewandt werden:
pp
/ / | \
/ / | \
p p2 p2 p4
/ | \ / | \ / | \ / | \
/ | \ / | \ / | \ / | \
[--------] [--------] [----------]
|
Wenn dies wegen u.U. zu schlechter Lesbarkeit nicht erfolgen soll, muss einfach in der Metrikbaum-Spezifikation eine weitere hierarchische Ebene eingezogen werden (s.a. Abschnitt 2.15.7):

Die Geschlossenheit des Synkopenmusters ist es auch, die einfachere Ansätze zur Lösung des Problems verunmöglicht, wie z.B. für jede metrische Position im Takt einfach eine "Menge von erlaubten Dauern" anzugeben, von denen dann der längste ausgewählt wird. Synkopen werden eben nur gewählt, wenn nichts an sie angebunden wird! Zeile "Nein" im folgenden ist zu ersetzen durch "ja":

Die soeben vorgestellten Zweier-Synkopen spannen von der Mitte des Intervalles des einen Elterknotens bis zur Mitte seines Nachfolgers, im selben Großelterknoten.
Es können aber auch Synkopenschreibweisen zweckmäßig sein, wo die beiden geteilten Knoten zwar im Vordergrund unmittelbar aufeinanderfolgen, -- das ist immer Voraussetzung --, aber im Mittelgrund durch mehr als eine Ebene getrennt sind. Diese nennen wir kurz "mehrfache Synkopen".
Man sehe das Extrembeispiel T.137f. aus Bruckners Dritter Sinfonie, Adagio, aus dem Vorgängerartikel, und die schrittweise Eliminierung dieser extremen Synkopen, geordnet nach Ebenen:

Der Stilparameter max_level_syncope_2 ist die Nummer der Generation, in der spätestens direkte Geschwister sein müssen. (Beim Wert null(0) sind alle Zweier-Synkopen verboten.) Wird der in diesem Beispiel aof zwei(2) begrenzt, ergibt sich Schreibweise P2, die gut lesbar scheint.
Dieselbe Regel führt auch für synkopierte Einzelnoten zu gerade noch brauchbaren
Ergebnissen (Zeile P2e). Das ist deshalb wichtig, weil der Algorithmus
damit auch kontext-frei gut arbeitet,
was eine sehr günstige Eigenschaft ist,
siehe oben Abschnitt 1.2 und die Diskussion
im Vorgängerartikel.
Hingegen ist der erste Takt von P1e mit den drei(3) überspannten Ebenen
kaum akzeptabel. Der dazugehörige Baum heißt ...
überspannte Ebenen:
pppp Ganze
/ \
/ \
ppp ppp Halbe DREI
/\ / \
/ \ /
pp pp Viertel ZWEI
/ \ / \
/ \ / \
p p Achtel EINE
/ \ / \
[----] <-- Achtel-Synkope
|
Punktierungen (als Sinne der Zusammenfassenden Transformation) sind nur möglich, solange die Elterknoten in aufsteigender Linie ausschließlich äquidistante Zwei-Teilungen aufweisen. Ganz oben kann evtl. eine andersartige Teilung stehen, bei der die beiden beteiligten Kind-Knoten aber ebenfalls gleichlang sind.
negative Punktierung:
pppp
/ ... / \ ... \ ... \
/ ppp xxx \
/ / \ \ \
/ pp xx \ \
/ \ \ \ |
p x \ \ |
/ \ \ \ \ |
a
[-------] | |
[-------------]| |
[-------------------]|
(. . . . . . . . . . . . .) <--GESCHW???
[----------]
positive Punktierung:
pppp
/ ... / \ ... \ ...
/ ppp yyy \
/ / \ /\
/ pp yy / \
/ \ / \ / \
k y / \ / \
/ \ / \ |
[------] | |
[--------------]| |
[------------------------]|
(. . . . . . . . . . . . . . . ) <--GESCHW???
[----------------------]
|
Die "x/xx" sind dabei die Tanten/Großtanten mit denen der Ausgangsknoten "a" verschmolzen wird. Diese müssen dieselbe Länge haben wie die die Eltern/Großeltern "p/pp", also ihre jeweiligen Geschwister, und können intern beliebig geteilt sein. Die beteiligten p/pp/... müssen hingegen immer äquidistant zweigeteilt sein.
Die "y/yy" sind die Tanten und Großtanten, mit derem erstem Kind der Startknoten "k" (oder der entsprechende Vorfahre) verschmolzen wird. Auch hier müssen die Beteiligten derselben Ebene gleichlang sein. Das jeweilige "y.." muss äquidistant zweigeteilt sein.
(Die mit "<--GESCHW??" markierten Zeilen zeigen je eine Dauer, für die es einen Konflikt zur Zusammenfassung von Geschwistern gibt, wie diskutiert unten in Abschnitt 2.16.)
Wird bis zu einer bestimmten Ebene "e" zusammenfasst, so wird die Dauer des dort herrschenden pp-Knotens notiert, und soviele Punkte angehängt wie "e" Ebenen über dem Ausgangsknoten liegt. Ein solcher "Dauern-Punkt" oder "Wert-Punkt" verlängert ja jene Dauer um die Hälfte, oder um die Hälfte der vorigen Verlängerung, s.o. Abschnitt 2.8, und realisiert so genau die benötigte Dauer.
Die Stilparameter max_dots_positive und max_dots_negative begrenzen die Anzahl der Punkte für negative und positive Punktierung. Für Pausen gilt zusätzlich max_dots_for_pauses.
Wird dieser überschritten, so werden statt einem halt mehrere Knoten in die Menge der erscheinenden übernommen, was entsprechend mehreren Dauernsymbolen im letztlichen Vordergrund entspricht. Der Stilparameter push_dots_down_not_up entscheidet, wie dabei die Verlängerungspunkte gruppiert werden: Falls ==true so wird zunächst für den kürzesten Knoten die maximale Anzahl von Punkten verwendet, und so weiter aufsteigend. Andernfalls für den längsten, absteigend.

Als "nett" (wie definiert oben in Abschnitt 2.3) können wir auch die Teilung durch vier(4) bezeichnen, da sie keine speziellen Probleme bei der Übertragung in die Vordergrundgestalt aufwirft.
Allerdings ergeben sich deutliche Unterschiede zwischen einer Teilung durch vier(4) und einer durch zwei-mal-zwei(2*2), wenn die voranstehend spezifizierten, schön einfachen Algorithmen angewandt werden. Dies zeigt sich in folgender Tabelle:
| Nr. | zwei mal zwei (2*2) | vier(4) | |
| A |

|
erzeugt als Synkope | erzeugt als Geschwister-Verschmelzung |
| B |

|
erzeugt als Punktierung | erzeugt als Geschwister-Verschmelzung |
| C |

|
erzeugt als Punktierung | NICHT ERZEUGT (nach obigem Algorithmus) |
| D |

|
NICHT ERZEUGT (nach obigem Algorithmus) | erzeugt als Punktierung |
| E |
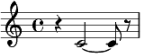
|
NICHT ERZEUGT (Synkopenmuster ist geschlossen) | erzeugt (Geschwister-Verschmelzung ist offen) |
| F |

|
NUR als mehrfache Synkope erzeugt | IMMER erzeugt (alles EINFACHE Synkopen) |
Man sieht sofort, dass in Verbindung mit den bisherigen Algorithmusdefinitionen beide Schreibweisen ihre Vor- und Nachteile haben:
Zeile C will man unbedingt haben, aber der einfache Algorithmus von oben fasst immer nur zwei zweigeteilte Elterknoten zusammen, hier wären im Falle der vier(4)-Teilung hingegen drei-einhalb Elterknoten zusammenzufassen.
Die synkopierte Punktierung in Zeile D will man eventuell haben, - in vielen Stilen ist diese sehr sinnvoll, siehe auch den folgenden Abschnitt.
Die Überbindung an die Synkope in Zeile E will man bestimmt nicht haben, das Synkopen-Muster ist nicht ohne Grund ein geschlossenes, weil es sonst mehr verwirrt als klärt (siehe Diskussion oben Abschnitt 2.15.4).
Die mehrfache Synkope (Viertel X in Zeile F) sollte auch nicht ungefragt generiert werden, sondern, wie oben ausgeführt, parametrisierbar ein- und ausschaltbar sein.
Zusammenfassend scheint die Modellierung als zwei(2)-mal-zwei(2) die bessere, denn hier ist lediglich die Zeile D als expliziter Sonderfall zu codieren, siehe Abschnitt 2.17.
Wenn versucht wird, die soweit beschriebenen Zusammenfassenden Transformationen auf
eine Initiale Repräsentation anzuwenden, können mehrere sich zwanglos kombinieren, in
dem sie auf verschiedene Unter-Intervalle desselben Ereignisses angewandt werden.
Es kann aber, ganz im Gegenteil, bei den ersten Schritten des Anwendungsversuches
schon Konflikte geben, wenn für verschiedene Transformationen die
Anwendungsbedingungen erfüllt sind und sie in Konkurrenz treten.
Beide Arten von Fällen zu klären dienen folgende Abschnitte.
Bei Zweier-Synkopen und Hemiolen ist nur ein Kindknoten je Elter überhaupt in der Initialen Überdeckung. Also konkurrieren nur die Dreier-Synkopen mit der Geschwister-Verschmelzung. Da aber die Synkopen ein geschlossenes Muster sind, bekommen sie einfach Priorität. Werden sie angewendet, so implizieren sie ja für die beiden Kind-Knoten, die auf derselben Seite des übersynkopierten Teilungsschlages liegen, deren Geschwister-Verschmelzung!
Hier kann ein Konflikt nur auf der obersten Ebene der Punktierung liegen, da nur dort durch mehr als zwei(2) geteilt werden kann und folglich nur dort Geschwister überhaupt verschmelzen können. Die Markierungen "<-GESCHW??" in voranstehenden Baumdiagrammen in Abschnitt 2.15.6 deuten das an, und die obigen Notenbeispiele Zeilen 5a bis 5d zeigen die Vordergrundgestalt des Problems: Mit der positiven Punktierung konkurrieren vorangehende gleich-lange Geschwister um den Knoten ppp; bei negativer Punktierung die nachfolgenden.
Beides kann auch kombiniert auftreten:

Derartige Konflikte treten, wie gesagt, da auf, wo eine größer-als-zwei-Teilung (>2) äquidistante Zweiteilungen beinhaltet. Also relativ häufig auf der obersten Ebene im verbreiteten 3/4- und 6/8-Takt.
Zur Zeit ist die Implementierung derart, dass positive Punktierung Vorrang
vor negativer und vor Geschwisterverschmelzung hat, und negative
Punktierung vor Geschwisterverschmelzung.
(Dies ist ein typischer Punkt an welchen evtl. weitere Stilparameter
einzufügen wären, wenn Forschung an Corpora dies nahelegt, s.a. unten
Abschnitt 3.2, Listenpunkt 1.)
Der Algorithmus kann für die Priorität zwei Flags vorsehen, für die positive
und die negative Punktierung vs. Geschwister. Soll eine weitergehende Differenzierung
des Punktierungsverhaltens im Fünfer-Fall vorgenommen werden,
so kann die fünf ja ersetzt werden durch "3+2" oder "2+3". Damit
sind sofort Geschwisterverschmelzung und Punktierung entsprechend dem gemeinten
Metrum eingeschränkt!
Es können positive und negative Punktierungen untereinander konkurrieren, wenn mehr als zwei Geschwister jeweils zweigeteilt sind, also in Dreier- und Fünferfolgen (oder Vierer, falls als solche erlaubt, s. Abschnitt 2.15.7):

Zur Zeit gewinnt die Positive Punktierung, aber vielleicht wird ein Stilparameter nötig werden (s.u. Abschnitt 3.2, Listenpunkt 1).
In bestimmten Grenzen scheint ein Notationsstil sinnvoll, der Zweier-Synkopen und Hemiolen mit (gleichsam "nachträglicher") Punktierung kombinieren kann:

Zeile SP1 ist allemal gut lesbar. Wird aber der Inhalt der Punktierungs-Ergänzung zu komplex (SP2), scheint irgendwann die Variante mit explizitem Haltebogen besser lesbar (SP3).
Im letzten Takt allerdings, dem Beispiel in 6/8, ist SP2 gegenüber SP3 zu bevorzugen. Die Bebalkung schafft doch eine grundlegend andere Ausgangsvoraussetzung der Lesbarkeit.
All diese Situationen sind besonders nur deshalb, weil die Teilungen "4"
als "2*2" und "6" als "3*2" realisiert sind. Deshalb
kann der oben beschriebene einfache Algorithmus
zur Punktierungserkennung nicht "unmittelbar" greifen.
Durch eine zeitweilige Linearisierung der obersten beiden Teilungsebenen in eine
einzige würde die geschilderten Punktierungen auf gleiche Weise wie
nicht-verschobene erkannt werden.
[[Dies ist zur Zeit noch nicht implementiert.]]
Die entsprechenden Bäume sind ...
Synkope und Punktierung:
ppp(4/4 = 2*2)
/ \ würde erkannt werden bei:
/ \
pp pp pp(4/4 = 4*1)
/ \ / \ / / \ \
/ \ p \ / / p \
/ \ / \ / / / \ \
[------]| [-------]
Hemiole und Punktierung:
ppp(6/4 = 2*3)
/ \ würde erkannt werden bei:
/ \
pp pp pp(6/4 = 6*1)
/ | \ / | \ / / / \ \ \
/ | \ p | \ / / / p \ \
/ | \ / \ / / / / \ \ \
[------]| [-------]|
|
[[Dies ist zur Zeit noch nicht implementiert.]]
Wegen der sehr freizügigen Regeln für die Gestalt des Metrikbaumes kann es durchaus sein, dass, hinausgehend über die konventionelle Verwendung, eine für den Elterknoten Notwendige Proportion bei einem Kindknoten wieder verschwindet. Dies ist möglich, da Faktoren im Nenner bei reiner Addition ja überleben, und die Folge der Kindknoten in unserem Modell durchaus heterogen sein kann:

Zeile hg0 zeigt den Ausgangsbaum.
Die in hg1 erscheinenden Knoten seien die oberste Ebene einer Alterative, tragen als
für sich selbst eine Notwendige Proportion über alle drei(3) Geschwister.
In hg2 erscheinen die heterogenen Folge von Kindknoten der nächsten Ebene.
Zeile hg3 soll lediglich verdeutlichen, dass die Viertelnote tatsächlich solche sind,
ohne jede Proportion, also in vier(4) Sechzehntel zerlegt werden können.
Soll ein Rhythmus wie in Zeile hg2 oder hg3 notiert werden, dann kann die lange Triolenklammer der oberen Ebene (wie in hg1) weggelassen werden und stattdessen die drei kürzeren "verselbständigten" Triolen wie in hg2.
Tritt aber die zweite Unterteilungsebene bei einem oder mehreren (>=1) Knoten der
obersten ebene garnicht in Erscheinung, dann wird überall dort eine je eigene
Triolenklammer gebraucht, wie in Zeile hg4. In diesem Falle ist die eine große
Triolenklammer vielleicht die bessere Wahl, was durch einen Stilparameter gesteuert
werden sollte.
Zeile hg5 zeigt, wie deren Wirkung dann bei einigen Unter-unter-Knoten kompensiert
wird. Diese Notwendigkeit von
Kompensation kann sich aber als Nachteil dieser Variante herausstellen.
Diese Entscheidung kann auch statisch getroffen werden, falls Zeile hg4
den Metrikbaum wiedergibt, also mindestens ein Knoten (hier: der mittlere)
Knoten keine heterogene Teilung aufweist, also allemal der großen Klammer
bedarf.
Allemal werden die notwendigen Entscheidungswege dieser Phase in
Phase Null-Zwei/Prop-Zwei so weit als möglich vorbereitet, s.o. Abschnitt 2.11.
Dass in zeitgenössischer Verwendung von CWN verselbständigte n-olen durchaus ergonomisch zweckmäßig sind, zeige folgendes Beispiel:

Da wir uns bisher "voll-kompositional" im Bereich der Rationalen Zahlen bewegen, können n-olen stets eliminiert werden durch Umschreiben auf einen größten gemeinsamen Teiler (d.i. eine hinreichend kleine Zählgröße) nebst entsprechender Anpassung des Tempos. So wird aus einer ungewöhnlichen Notation (Zeile T) eine stärker konventionelle (Zeile X).
Diese Äquivalenz zeigt zunächst nur, dass Zeile T nicht völlig aus der Luft gegriffen ist. Es kann aber weiterhin sogar sein, dass X dem psychischen Empfinden weniger adäquat ist, also weniger ergonomisch zweckmäßig. Seien z.B. alle auftretenden Schläge intern immer zwei(2)-geteilt, siehe Zeilen Tu und Xu. Es induzieren die Zeilen T und Tu einfach das Spielgefühl "drei Viertelschläge, dann drei Viertel-Triolen-Schläge, von denen der letzte übersprungen (/weggelassen) wird." Diese Proportion ist u.U. deutlich einfacher umzusetzen als die Variante X/Xu, die zwar rein arithmetisch äquivalent ist, aber etwas "stark synkopen-haftes" in der ersten Takthälfte vermuten läßt, und damit ein ganz anderes Spielgefühl.
Zu Beginn dieser Phase haben wir für jedes Eingabe-Ereignis eine Menge von Knoten aus dem Metrikbaum: Eine vormals "lückenlose" Folge einer Überdeckung von einer seiner möglicherweise vielen Varianten, die durch Zusammenfassende Transformationen ausgedünnt wurde.
Diese Knotenfolge wird nun in Dauernsymbole übersetzt, und in korrekter Schachtelung
mit den n-olen-Klammern ausgegeben.
Technisch gibt es in der Implementierung dafür einen "Visitor", der folgende Methoden
anbietet:
Die ersten drei Methoden müssen vom Benutzer überschrieben werden, dann die letzte aufgerufen.
Die Klammer-Methoden bedeuten einfach das Öffnen und Schließen einer Klammer mit der entsprechenden Proportion. (Man beachte dass eine Rationale Zahl die Klammer determiniert, also ein gekürzter Bruch. "9/6" o.ae.ist also derzeit nicht möglich.)
Die writeOut()-Methode steht für je ein Dauersymbol. Dabei wird das Dauernsymbol, der momentan gültige Proportionalfaktor und die Nummer des originalen Eingabeereignisses mitgegeben, zusätzlich ob es Klang, nicht Pause ist, ob es das erste Symbol dieses Ereignisses ist, und ob es das letzte.
Die Ereignisnummer erlaubt dem Benutzer-Code das originale Ereignis zu identifizieren und so alle weiteren für die Ausgabe nötigen Parameter. Die Information "Klang, nicht Pause" wird also nur der Bequemlichkeit halber mitgegeben. Die Information ob erstes oder letztes Klangsymbol ist deutlich wichtiger, genau dies will der Benutzer ja vom Algorithmus erfahren. Beim ersten Symbol müssen z.B. Lautstärken eingetragen werden, beim letzten kein Haltebogen, etc. 12
In Phase Merge wurde schon darauf geachtet, dass die Ergebnisse einer Zusammenfassenden Transformation e-schreibbar sind. Dies braucht aber für nicht-transformierte Knoten, also solche, die direkt der Initialen Überdeckung stammen, nicht der Fall zu sein, -- die Regeln für Metrikbäume erlauben beliebige Dauern.
Der Algorithmus dieser Phase arbeitet wie folgt:
Die Entscheidung zwischen C und F ist wieder eine heuristische
(vgl. Abschnitt 1.2):
Wenn eine Dauer schon zerlegt werden muss, dann ist es
grundsätzlich ergonomisch zweckmäßig, der Struktur der Kindknoten zu folgen.
Das kann aber deutlich mehr Dauernsymbole kosten als eine MFZ, z.B. wenn
die Dauern der Kindknoten ebenfalls nicht e-schreibbar sind.
Also kann irgendwann eine knappe MFZ, obwohl sie quer zum Metrikbaum steht,
ergonomisch zweckmäßiger sein.
Für diese Entscheidung gibt es zwei Stilparameter,
die angeben, wieviele Dauernsymbole in C
maximal enthalten sein dürfen, damit dieser Lösungsvorschlag gewählt wird:
max_childs_to_print ist eine absolute Größe,
max_childs_over_free_sectioning gibt an wieviel C mehr als F haben darf.
[[Dies ist zur Zeit noch nicht implementiert.]]
Wird einer der Werte überschritten, wird F gewählt.
Die letzte Regel (diesen Abschnitt, Liste 2, Listenpunkt 7) verhindert unendliche Rekursion: Bei äquidistanter Zweiteilung herrscht auf der Ebene der Kinder ja genau dasselbe Darstellungsproblem wie bei k, nur mit verdoppeltem Nenner. Also könnte von einer Berechnung von C niemals eine Lösung kommen.
Damit ist der metricSplit Algorithmus vollständig abgelaufen.
Zukünftige wünschenswerte Erweiterungen finden sich in Abschnitt 3.2.
Wenn eine Dauer a/b (Rationale Zahl) an einer
Stelle schreibbar ist, an der die Proportion (m/k) herrscht,
dann wird sie geschrieben als
c/d=(a/b)*(k/m).
c/d enthält also nur Zweierpotenzen im Nenner, und soll nun ohne Hilfe einer weiteren Proportion geschrieben werden, also in Dauernsymbole übersetzt.
Für die Frage der Schreibbarkeit ist unter diesen Voraussetzungen (wie schon erwähnt) nur der Wert des Zählers relevant. Aus diesem ergeben sich zunächst keine grundlegenden Einschränkungen: Der Haltebogen zwischen zwei Dauernsymbolen bedeutet, wie erwähnt, die Addition von deren Dauernwerten. Es ist also möglich, jeden beliebigen Zähler einer rational gegebenen Dauer zu notieren, schlimmstenfalls durch wiederholte Addition von "eins(1)".
Nicht-trivial sind hingegen die Fragen nach den minimalen Schreibweisen, also nach der Schreibweise mit möglichst wenig Summanden/Dauernsymbolen.
Gibt es ein p>=1, sodass c=(2^p)-1, also c aus {1,3,7,15,31,63, ...}, so ist c/d e-schreibbar und p-1 ist die Anzahl der benötigten Verlängerungspunkte.
Andernfalls muss die Dauer c/d durch Summenbildung mit Haltebögen dargestellt werden. Wir nennen Minimale Freie Zerlegung (MFZ) eine Folge minimaler Länge aus Dp (also aus eventuell punktierten Dauernsymbolen, siehe die Definition oben Abschnitt 2.8), deren Summe c/d ergibt.
Das Wort "frei" bedeutet dabei, dass bei dieser Art von Zerlegung der Metrikbaum nicht berücksichtigt wird.
Da die Nenner immer Zweierpotenzen sind und c/d als Rationale Zahl gekürzt ist. treten für c nur ungerade Werte auf. Ausserdem ist der Nenner für die Ermittlung irrelevant, wir suchen also als "MFZ(c)" nur eine Folge von Summanden für den Zähler, die dann jeweils entsprechend eingesetzt werden kann.
Gehen wir aus von den Elementen in Dp, und dem darzustellenden Zähler c in binärer Zahlen-Darstellung: Die Zähler der Werte in Dp sind {1, 3, 7, 15, ..., 2^n-1}, und bilden als binäre Zahl eine zusammenhängende Folge von Einsen. Diese beginnen "ganz rechts" an der "Stelle Nummer 0" mit dem Stellenwert "1". Multipliziert man sie mit einer Zweierpotenz 2^m, so bedeutet das ein Verschieben dieser Folge nach links um m Stellen.
Besteht die Binärdarstellung von c nun aus "k" verschiedenen solchen
zusammenhängenden Folgen von Einsen, jeweils getrennt durch mindestens eine
Ziffer Null,
so ist ein naheliegender erster Kandidat CAND(c) für
MFZ(c) eine Menge aus k verschiednenen
Werten aus Dp, von denen jeder einer maximalen zusammenhängenden Kette
von Einsen in jener Binärdarstellung entspricht.
Jeder dieser Werte ist ein Produkt aus einem der Zählerwerte 2^n-1,
entsprechend der Anzahl der Einsen, und einer Zweierpotenz 2^m,
entsprechend der Positionsverschiebung der niederwertigsten dieser
Einser:
// Ketten von Einsern: 1 11 111 1111 11111
// c= k= c= L=
0000 0001 1 1 1*1 1
0000 0011 3 1 1*3 1
0000 0101 5 2 4*1+1*1 2
0000 0111 7 1 1*7 1
0000 1001 9 2 8*1+1*1 3<<<
0000 1011 11 2 8*1 +1*3 2
0000 1101 13 2 1*1 +4*3 1
0000 1111 15 1 1*15 1
0001 0001 17 2 16*1+1*1 3<<<
0001 0011 19 2 16*1 +1*3 3<<<
0001 0101 21 [3] 16*1+4*1+1*1 2-----
0001 0111 23 3 16*1 +1*7 2
0001 1001 25 2 1*1 +8*3 1
0001 1011 27 2 1*3+8*3 1
0001 1101 29 2 1*1 +4*7 1
0001 1111 31 1 1*31 1
|
Durch simples Auslesen der längsten zusammenhängenden Einer-Kette enthält man Zerlegungen wie in obenstehender Tabelle. Im Fall einer Zerlegung, die aus zwei(2) Summanden, also Einer-Gruppen besteht, ist diese bestimmt eine Lösung, also eine minimale Summandenmenge, aber u.U. nicht die einzige; sie kann in eine(1) oder zwei(2) andere überführt werden. Dabei entstehen die trennenden Nullen zwischen den Einser-Gruppen durch Überlauf bei der Addition:
XKM MMP XKM MMP XKM MMP
0010 0000 00oi iii0 00o0 00i0
+ 0000 0001 + 0000 00i1 + 000i iii1
-------------- ----------- -----------
0010 0001 0010 0001 0010 0001
|
Die neueingeführten Einser werden dargestellt als "i", die Nuller als "o".
Die Umwandlung geschieht durch Ersetzung der die beiden Einer-Gruppen
trennenden Nullen. In beiden Summanden wird die niedrigste dieser Nullen durch
eine Eins ersetzt (Stelle "P").
In einem der beiden Summanden werden auch alle übrigen dieser Nullen durch Eins ersetzt
(Stellen "M"). Die Einsen an den Stellen P und M ergeben bei der Addition nun
wieder Nullen.
Die niederwertigste Eins des höherwertigen Summanden wird durch Null ersetzt und
ensteht in der Summer wieder als Überlauf, an Stelle "K".
In ebendiesem Summanden muss an der nächst-höheren Stelle "X"
allerdings schon wieder eine Null stehen! Denn eine dort
stehende Eins würde ja nach dieser letzten Ersetzung einen dritten Summanden erzeugen,
und das Transformationsergebnis hätte eine Einer-Gruppe mehr, wäre also keine
minimale Zerlegung.
Also muss der obere Summand eine Einer-Gruppe der Länge 1(eins)
sein, eine einfache Zweierpotenz.
Eine Entscheidungsmöglichkeit, in welcher der beiden Summanden die Stellen
"M" durch Einsen gefüllt werden, besteht nur, wenn die trennende Nuller-Gruppe
länger als eins(>1) ist, es also überhaupt Stellen "M" gibt.
Nennen wir dieses Verfahren der Ableitung weiterer Lösungen "KMP-Verfahren".
Es gilt also für die Anzahl der Lösungen L, soweit bisher betrachtet:
Das KMP-Verfahren hat durchaus praktische Relevanz in der Notation von Musik. Die verschiedenen Summen ...
XKP XKP X KMP X KMP X KMP 0000 0100 0000 0010 0000 1000 0000 0110 0000 0010 + 0000 0001 + 0000 0011 + 0000 0001 + 0000 0011 + 0000 0111 ------------ ----------- -------------- ----------- ----------- 0000 0101 0000 0101 0000 1001 0000 1001 0000 1001 |
...eingesetzt als Nenner von "/16", stehen für die je nach Kontext zu bevorzugenden Notationsvarianten ...


Das KMP-Verfahren funktioniert auch bei k=3, angewandt auf zwei der drei Summanden,
auch auf die nicht unittelbar benachbarten, da die Addition ja assoziativ ist.
Heissen diese von unten nach oben A, B und C.
Stehe (XY) für die Anwendung auf die Gruppen X und Y, bei mehr als
einer (>1) trennende Null, wobei X die Einer
an den M-Positionen zugeschlagen bekomme. Die neuentstehenden Gruppen heißen X' und
Y' (oder X2 und Y2, bei wiederholter Anwendung, s.u.).
Bei nur einer trennenden Null(=1) gibt es nur eine Applikationsmöglichkeit,
die wir (STS) schreiben. (Dabei ist S meist die niederwertige Gruppe.)
Im Falle von k=3 kommen zu der einen Ausgangslösung CAND(c) noch hinzu:
Maximal könnten also sechs(6) weitere Lösungen dazukommen:
Gruppe C =1 Lücke C-B =1 (l0=3) Gruppe B =1 Lücke B-A =1 (l1=1) L=5
Lücke B-A >1 (l1=2) L=6
Gruppe B >1 (l1=0) L=4
Lücke C-B >1 (l0=4) Gruppe B =1 Lücke B-A =1 L=6
Lücke B-A >1 L=7
Gruppe B >1 L=5
Gruppe C >1 (l0=0) Gruppe B =1 Lücke B-A =1 L=2
Lücke B-A >1 L=3
Gruppe B >1 L=1
|
0010 1001 = 41 ist das numerisch niedrigste Beispiel mit zunächst sechs(6) Minimalen Freien Zerlegungen (nicht etwa 0010 0101=37, s.u.!):
orig (BA) (AB) (BCB) (AC) (CA)
KMP KMP KP KM MMP KM MMP
A 0000 0001 0000 00i1 0000 0ii1 0000 0001 000i iii1 0000 00i1
B +0000 1000 +0000 oii0 +0000 o0i0 +000i 1000 +0000 1000 +0000 1000
C +0010 0000 +0010 0000 +0010 0000 +00oi 0000 +00o0 00i0 +00oi iii0
---------- ---------- --------- ---------- ---------- ----------
0010 1001 0010 1001 0010 1001 0010 1001 0010 1001 0010 1001
|
0100 1001 = 73 ist das numerisch niedrigste Beispiel mit zunächst sieben(7) Minimalen Freien Zerlegungen:
orig (BA) (AB) (BC) (CB) (AC) (CA)
KMP KMP KMP KMP KMM MMP KMM MMP
A 0000 0001 0000 00i1 0000 0ii1 0000 0001 0000 0001 00ii iii1 0000 00i1
B +0000 1000 +0000 oii0 +0000 o0i0 +00ii 1000 +000i 1000 +0000 1000 +0000 1000
C +0100 0000 +0100 0000 +0100 0000 +0o0i 0000 +0oii 0000 +0o00 00i0 +0oii iii0
---------- ---------- --------- ---------- ---------- ---------- ----------
0100 1001 0100 1001 0100 1001 0100 1001 0100 1001 0100 1001 0100 1001
|
Aber tatsächlich explodiert bei k=3 die Anzahl der Möglichkeiten! Man sieht nämlich sofort sofort, dass neue hochstehende Einergruppen auftreten, resp. alte überleben, sodass das KMP-Verfahren wiederholt angewandt werden kann.
In den Fällen (AB) und (BA) überlebt die obere Gruppe C mit ihrer einen(1) Eins.
Vorüberlegung:
Sei S niederwertiger als T und T einstellig.
a) Seien S und T durch mindestens zwei Nullen (>=2) getrennt,
es gibt also M-Stellen.
Durch Anwendung (TS) entsteht keine Einergruppe der Länge =1,
da S' die neue Eins an Stelle P und ihre mindestens eine ursprüngliche Eins
bei Stelle (P-1) hat, und T' mehr als eine Eins an den Stellen P und M.
Aber in (ST) wird T' zu einer einfachen Eins("i") an Position P.
Dabei ist P bestimmt durch die erste Null über der niederwertigen Gruppe S.
(ST) (TS)
KM MP KM MP
S 00 001 0i ii1 00 0i1
T 10 000 o0 0i0 oi ii0
|
b) Bei (STS) entsteht immer eine solitäre Eins in T'.
(STS)
KP
S 001 0i1
T 100 oi0
|
Nach der Anwendung (AB) in den obigen Beispielen kann dies nicht ausgenutzt werden,
da das entstehende B' keinen unteren Nachbarn mehr hat.
(Dafür überlebt dort die Einergruppe C!)
Aber in (BC) ist A der untere Nachbar und in (AC) ist B der obere
Nachbar von C'.
Ausserdem bleibt in (CA) das unbeeinflusste B ein oberer Nachbar von A', nur
dass die Nuller-Lücke geschrumpft ist.
Folglich kann das KMP-Verfahren ein zweites Mal angewandt werden,
In (AB) und (BA) auf C und A' oder B';
in (BCB) auf C' und A;
in (AC) auf B und C'.
in (CA) auf B und A'.
(Wir schreiben "X2" und "X3" für die bei den weiteren Applikationen aus "X" entstehenden Einer-Gruppen.)
Dies führt bei den bisherigen sechs(6) MFZ von 41 zu folgenden weiteren 12 Lösungen:
A' 0000 0011 (BA) A' 0000 0111 (AB)
B' +0000 0110 B' +0000 0010
C +0010 0000 C +0010 0000
KM MP (BA)(AC) KM P (AB)(AC)
A'2 000i ii11 A'2 000i i111
B' +0000 0110 B' +0000 0010
C2 +00o0 0i00 C2 +00o0 i000
---------- ----------
=0010 1001 =0010 1001
KM MP (BA)(CA) KM P (AB)(CA)
A'2 0000 0i11 A'2 0000 i111
B' +0000 0110 B' +0000 0010
C2 +00oi ii00 C2 +00oi i000
---------- ----------
=0010 1001 =0010 1001
KM P KM MP
A' 0000 0011 (BA)(BC) A' 0000 0111 (AB)(BC)
B'2 +000i i110 B'2 +000i ii10
C2 +00o0 i000 C2 +00o0 0i00
--------- ---------
=0010 1001 =0010 1001
KM P KM MP
A' 0000 0011 (BA)(CB) A' 0000 0111 (AB)(CB)
B'2 +0000 i110 B'2 +0000 0i10
C2 +00oi i000 C2 +00oi ii00
--------- ---------
=0010 1001 =0010 1001
----------------------------------------------------------------
A 0000 0001 (BCB) A' 0001 1111 (AC)
B' +0001 1000 B +0000 1000
C' +0001 0000 C' +0000 0010
K MMP (BCB)(CA) KP (AC)(BCB)
A2 0000 00i1 A' 000i i111
B' +0001 1000 B2 +0000 oi00
C'2 +000o iii0 C'2 +0000 0i10
---------- ----------
=0010 1001 =0010 1001
K MMP (BCB)(AC)
A2 0000 iii1 --------------------------------------
B' +0001 1000
C'2 +000o 00i0 A' 0000 0011 (CA)
---------- B +0000 1000
=0010 1001 C' +0001 1110
KP (CA)(ABA)
A'2 0000 0i11
B2 +0000 oi00
C' +0001 1110
----------
=0010 1001
|
Eine ähnliche Überlegung führt dazu, dass auf (BA)(BC) C2 als Solitär über A' und in (AB)(AC) über B' entsteht, und deshalb das KMP-Verfahren ein drittes Mal angewandt werden kann:
(BA)(BC) (AB)(AC)
A' 0000 0011 A'2 0001 1111
B'2 +0001 1110 B' 0000 0010
C2 +0000 1000 C2 0000 1000
(BA)(BC)(ACA) (AB)(AC)(BCB)
KP KP
A'3 0000 0i11 A'2 0001 1111
B'2 +0001 1110 B'3 +0000 0i10
C23 +0000 oi00 C23 +0000 oi00
---------- ----------
=0010 1001 =0010 1001
|
In Noten übersetzt, bezogen auf 64tel, von links nach rechts gelesen, also immer die längste voran:

Es scheint also zunächst 6+12+2=20=18 Lösungen zu geben.
Allerdings gilt (was man am bequemsten an den Notensymbolen ablesen kann !-):
(AC)=(AB)(AC) = 4.... + 8
(BA)(AC) = (AC)(BC) = (AB)(AC)(BCB) = 4.... + 16.
(CA)=(BA)(BC) = 4... + 8
(AB)(BC) = (CA)(AB) =(BA)(BC)(ACA) = 4... + 16..
(BA)(CA)=(AB)(CB) = 4.. + 16..
(AB)(CA) = (BC)(AC) = 4. + 8...
(BA)(CB)=(BC)(CA) = 4. + 8..
Es bleiben also 20-9=11 verschiedene Lösungen.

Bei den bisherigen sieben(7) MFZ von 73 folgt die wiederholte Anwendung zu folgenden weiteren Lösungen:
A' 0000 0011 (BA) A' 0000 0111 (AB)
B' +0000 0110 B' +0000 0010
C +0100 0000 C +0100 0000
KMM MP (BA)(AC) KMM P (AB)(AC)
A'2 00ii ii11 A'2 00ii i111
B' +0000 0110 B' +0000 0010
C2 +0o00 0i00 C2 +0o00 i000
---------- ----------
=0100 1001 =0100 1001
KMM MP (BA)(CA) KMM P (AB)(CA)
A'2 0000 0i11 A'2 0000 i111
B' +0000 0110 B' +0000 0010
C2 +0oii ii00 C2 +0oii i000
---------- ----------
=0100 1001 =0100 1001
KMM P KMM MP
A' 0000 0011 (BA)(BC) A' 0000 0111 (AB)(BC)
B'2 +00ii i110 B'2 +00ii ii10
C2 +0o00 i000 C2 +0o00 0i00
--------- ---------
=0100 1001 =0100 1001
KMM P KMM MP
A' 0000 0011 (BA)(CB) A' 0000 0111 (AB)(CB)
B'2 +0000 i110 B'2 +0000 0i10
C2 +0oii i000 C2 +0oii ii00
--------- ---------
=0100 1001 =0100 1001
----------------------------------------------------------------
A 0000 0001 (BC) A' 0011 1111 (AC)
B' +0011 1000 B +0000 1000
C' +0001 0000 C' +0000 0010
K MMP (BC)(CA) KP (AC)(BC)
A2 0000 00i1 A' 00ii i111
B' +0011 1000 B2 +0000 oi00
C'2 +000o iii0 C'2 +0000 0i10
---------- ----------
=0100 1001 =0100 1001
K MMP (BC)(AC)
A2 0000 iii1 --------------------------------------
B' +0011 1000
C'2 +000o 00i0 A' 0000 0011 (CA)
---------- B +0000 1000
=0100 1001 C' +0011 1110
KP (CA)(AB)
A'2 0000 0i11
B2 +0000 oi00
C' +0011 1110
----------
=0100 1001
|
Auch hier erlauben (BA)(BC) und (AB)(AC) eine dritte Anwendung, was also zunächst 7+12+2=21 Lösungen ergibt, unter denen wiederum Doubletten auszusondern wären, etc.

Es kann aber auch das Gegenteil gelten, eine "Implosion", dass nämlich CAND(c), die naive einfache Zerlegung in Einer-Gruppen laut Tabelle, gar keine Lösung ist, da die Anzahl der Summanden nicht minimal ist. Im o.e. abstrakten Fall (ST) wird das (höherwertige) T ja zu einer solitären Eins an Stelle P, bei (TS) ist diese Eins das obere Ende von S'.
Sind nun im konkreten Fall A und B nur durch eine einzige (=1) Null getrennt, dann steht diese genau an der Stelle P, wenn die Transformation auf A und C angewandt wird. Im Falle (AC) verschmelzen B und C', im Falle (CA) verschmelzen B und A':
XK MMP (AC) XK MMP (CA) XK MMP
A + 0000 0001 + 0000 iii1 + 0000 00i1 \
B + 0000 0100 + 0000 0100 \ + 0000 0100 /
C 0001 0000 000o 00i0 / 000o iii0
-------------- ----------- -----------
0001 0101 0001 0101 0001 0101
|
Es gibt im Fall von drei Einer-Gruppen, bei denen die unteren beiden nur durch eine(1) Null getrennt sind und die oberste nur eine(1) Eins hat, also nur zwei(2) Lösungen. Diese benötigen allerdings einen Summand weniger als die ursprüngliche naive Einer-Gruppen-Zerlegung, nämlich nur zwei(2).
Die frühest auftretenden dieser Fälle sind
0001 0101 = dezimal 21 0010 0101 = dezimal 37 0010 1101 = dezimal 45 0100 0101 = dezimal 69 0100 1101 = dezimal 77 etc. |

Sowohl die explodierenden Lösungen mit k=3 ab 47, als auch die schrumpfenden ab 37 werden zur Zeit ignoriert. Der metricSplit-Algorithmus behandelt die Bildung des MFZ "heuristisch" im Sinne der Unterscheidung von Abschnitt 1.2: ausschließlich die Einundzwanzig(21) wird fest auf 15+6 oder 14+7 abgebildet. Für alle anderen Nenner wird CAND(c) als Zerlegung geliefert, da wir diese z.Zt. im Kontext der praktischen Anwendung von CWN für äußerst selten halten.
In theoretischer Hinsicht scheinen allerdings weitere Verallgemeinerung dieser Ergebnisse durchaus wünschenswert.
MetricSplit ist zur Zeit in Java implementiert und Teil
des Projektes
BandM Models of Music. [bandmMusic]
Dabei dient es zunächst dazu, Ergebnisse von algorithmischem Komponieren zu
visualisieren, indem Quelltexte für das Notensatzprogramm Lilypond generiert
werden. [lilyPond]
Andere "back-ends", wie "Music XML", sollen folgen.
Neben der praktischen ist ja, wie zu Beginn erwähnt, auch durchaus eine theoretische Nützlichkeit angestrebt.
Es scheint durchaus sinnvoll, gegebene Corpora der Musikgeschichte
(Manuskripte oder Drucke) zu versuchen, mit MetricSplit nachzurealisieren,
indem die Parametereinstellungen gefunden werden, die möglichst ähnliche
Resultate zeitigen.
Dies kann Erkenntnisse bringen in zwei diametral entgegengesetzte Richtungen:
Einmal (a) über die Corpora selber, ihre Systematik, Vergleichbarkeit,
innere Konsistenz, etc., vielleicht sogar über den geistigen Zustand, die
Entwicklung des Autors.
Dann aber auch (b) über den Algorithmus selbst, über häufig merkliche Defizite,
die eine entsprechende Weiterentwicklung wünschenswert machen.
Im voranstehenden Text wurden schon etliche Punkte erwähnt und verortet, die der Implementierung harren, und die hier zwecks Übersicht noch einmal zusammengefasst seien:
Bei nächster Gelegenheit werden wir, Inschallah, diese Punkte sukzessive abarbeiten.
Man kann sich mit einem Klick auf http://bandm.eu:/metatools/download/DemoMetric.jnlp die Java-Applikation DemoMetric herunterladen, die es erlaubt, mit dem Algorithmus zu spielen.
Das erscheinende GUI zeigt drei "Karteikarten": Auf der ersten trage man die Formel für die Metrikbaum-Spezifikation ein. Die beiden Fenster darunter zeigen den Metrikbaum, das linke in seinem Originalzustand, das rechte beim "Lernen".
Auf der zweiten Karteikarte kann ein Rhythmus als Dauern- oder als Zeitpunkt-Folge eingegeben werden. Die Eingabe wird in die jeweils andere Form umgerechnet und normiert.
Drückt man dort "Return", oder in der dritten Eingabezeile, die zwischen Klang und Pause zu unterscheiden erlaubt ("s" oder "p"), dann erscheint unten der Visitationsablauf, und auf einer dritten Karteikarte ein generierter Lilypond-Quelltext [lilyPond].
((Diese Applikation ist noch in der Entwicklung und ihre Handhabung kann sich noch wenig, ihr Leistungsumfang sehr verändern!--))
((Anmerkung fuer Windows-User:
Die Applikation benötigt Java-ACHT, welches evtl. auf Ihren Rechner erst
heruntergeladen werden muss. Dieser Prozess wird durch Anklicken des o.e.
Jnlp-Links i.A. automatisch
eingeleitet: Man wird auf eine Browser-Seite geleitet, von der man
die "Java-Acht-Installations-.exe-Datei" erhält, die man schlicht ausführen muss.
(Dabei alle Bedingungen akzeptieren !-)
Das Kontroll-Panel befindet sich seit Java-Acht nicht mehr in der "Systemsteuerung",
sondern in "Taskleiste->All Programme->Java->Java konfigurieren".
Dort muss unter "Sicherheit -> Site-Liste bearbeiten" die Quell-Site
"http://bandm.eu" als AUSNAHME eingetragen werden, damit DemoMetric durch
den Sicherheitscheck geht.
))
Viel Spaß.
Fassen wir hier die gemeinsamen Probleme wechselseitigen Beeinflussungen von E-Schreibbarkeit und Zusammenfassenden Transformationen noch einmal zusamen.
Zunächt zur Erinnerung: an jeder Stelle im Ausgabeprozess, an der eine Dauer "p/q" zu
notieren ist, sind alle in derem Nenner auftretenden Faktoren != 2^n bereits
durch umgebende Proportionen/n-olen-Klammern realisiert und aus dem zu notierenden Wert
herausgerechnet.
Es bleibt also einzig der Zähler kritisch. Wenn die Dauer "e-schreibbar" ist
(also als ein einziges(1) CWN-Dauernsymbol schreibbar), dann hat dieser die Form
2^n-1, für irgend ein n. Dabei ist (n-1) die Anzahl der auftretenden
Verlängerungspunkte. Diese Zahlen sind
alle rechtsbündig beginnenden
geschlossene Einerketten in Binärdarstellung,
Man sieht im folgenden sehr schön die Windschiefigkeit von historischer Entwicklung und praktischer Anwendung: Erfunden wurde der Verlängerungspunkt im Frühbarock (wahrscheinlich als schludrige Form des Haltebogens) für die "punktierten Rhythmen" drei-zu-eins, sieben-zu-eins, etc., in diesen festen Kontexten. Heute allerdings kann diese Schreibweise, davon "abstrahiert", schlichtweg verwendet werden, um in beliebigem Kontext die Nenner drei(3), sieben(7), fünfzehn(15) etc. auszudrücken.

Zur Orientierung seien die hier relevanten Eigenschaften der beteiligten Kind- und Elterknoten (K-und E-Knoten) nochmals aufgeführt, die zur Anwendbarkeit der verschiedenen Zusammenfassenden Transformationen vorliegen müssen:
| Transformationsmuster | Allg. Bedingung der Anwendbarkeit | UND: |
| Zweier-Synkope | E-Knoten gleichlang | beide äquidistant zwei(2)geteilt |
| Dreier-Synkope und Hemiole | E-Knoten gleichlang | beide äquidistant drei(3)geteilt |
| Punktierung | die zwei je Ebene beteiligten E-Knoten gleichlang | alle Vorfahren des kürzesten beteiligten Knotens (aufsteigend bis zum ersten für alle beteiligten gemeinsamen) äquidistant zweigeteilt |
| n Geschwister | K-Knoten gleichlang |
Die E-Schreibbarkeit der resultierenden Dauer ergibt sich durch die Kombination der Dauer der beteiligten (resp. des kürzesten beteiligten) Kind-Knotens und dem letztlich auf diese anzuwendenden Faktor. Dieser hängt von der Art der Zusammenfassenden Transformations ab. Aufgeschlüsselt nach diesem Faktor stellen sich die Bedingungen dar als ...
| Faktor | Transformation | Bedingung für E-Schreibbarkeit des Resultates |
| 2 o. 4 | Zweier-Synkope, Hemiole,
zwei o. vier Geschwister |
K-Dauer e-schreibbar |
| 3 | Dreier-Synkope,
drei Geschwister |
K-Dauer als Grundsymbol schreibbar
(oder Spontane Ausnahmen, wie K-Dauer=5) |
| 5 | Fünfer-Synkope | (oder Spontane Ausnahmen, wie K-Dauer=3) |
| 3,5,7,15... | Punktierung | K-Dauer als Grundsymbol schreibbar
(oder Spontane Ausnahmen wie 3*5, 7*9) |
Selbstverständlich sind alle Faktoren der Form 2^n unkritisch: Ist die K-Dauer e-schreibbar, ist es auch das Produkt, also das Transformationsresultat, und auch umgekehrt.
Für alle Faktoren der Punktierungen (also 2^n-1, also 3,7,15,31 etc.)
gilt, dass das Resultat e-schreibbar ist, wenn die K-Dauer
eine Grund-Dauer ist ("g-schreibbar").
Wenn die K-Dauer bereits punktiert ist, führen sie niemals zur E-Schreibbarkeit.
Ansonsten (K-Dauer ist ungerade, aber nicht 2^n-1) gibt es grundsätzlich keine
E-Schreibbarkeit, aber Spontane Glückliche Ausnahmen.
So z.B. für den Faktor fünf(5) und neun(9), s. die folgenden Beispiele.
Wichtig für den Zusammenhang ist die erwähnte Tatsache,
dass punktierte Werte nicht
punktiert werden können.
Dies ist gleichbeutend mit dem Satz, dass
ein Produkt (2^a-1)*(2^b-1) für a,b>=2 niemals als
[Verschiebung von] (2^x-1) darstellbar ist.
Das zeigt sich am einfachsten bei der Betrachtung der Binärziffern: beide Faktoren sind
geschlossene Einerketten, beginnend bei Stelle null. Berechnet man die
Multiplikation als mehrfache Addition, dann sieht die "rechte obere Ecke"
davon immer so aus:
.... xx11
...x x11
..xx 11
etc....
+______________
.... ..01
|
...und zwar völlig unabhängig von xx, also den höheren Bits von a und b.
Da die Stelle null eine Eins aufweist, die Stelle eins eine Null, und zweifellos
noch höhere Einsen erscheinen werden, entsteht niemals eine zusammenhängende
Einerkette, auch nicht durch Kommaverschiebung.
Die konkrete Konsequenz für unser Problem ist, dass wenn die Kind-Knoten schon punktierte Dauern haben, die Zusammenfassende Transformation der Punktierungen (ein- oder mehrfach) nicht anwendbar sind.
Eine hier noch nicht implementierer Lösungsanatz wäre die Verwendung von
zusätzlichen Abkürzenden Proportionen. Dies sind lt. Definition in Abschnitt 2.10 solche, die durch additive Schreibweise ersetzt werden können, die sich
also (im Ggs. zu den Notwendigen Proportionen) auf Zähler statt Nenner beziehen. Mit
diesen könnten die Punktierungen der K-Knoten eliminiert werden, so das diese zu
Grundsymbolen werden, und dann die Punktierung ganz wie üblich angewandt werden, siehe
Beispiele unten in Abschnitt 5.3.
[[Dies ist zur Zeit noch nicht implementiert.]]
Ist über dem entsprechenden Bereich bereits eine Notwendige Proportion aktiv, so können evtl. zum Zwecke der Lesbarkeit beide Proportionen vereinigt werden, zu einer Gemischten.
Dieses Vorgehen ist aber i.A. nur dann uneingeschränkt anzuwenden, wenn nicht "weiter unten" im zu notierenden Rhythmus doch noch kürzere Dauernwerte auftreten, welche des ursprünglichen Zählers durchaus bedürfen, und nur durch eine weitere, geschachtelte Proportion notierbar sind, welche die gerade neu eingeführte rückgängig machen muss. Auch dazu folgen unten Beispiele.

Die lustigen Spontanen Ausnahmen für "E-Schreibbarkeit trotz krummer Faktoren und krummer K-Dauern" zeigen sich in folgender Multiplikations-Matrix, in der die e-schreibbaren Werte hervorgehoben sind.
| X[3] | 5 | X[7] | 9 | 11 | 13 | X[15] | 17 | |
| X[3] | 9 | X[15] | 21 | 27 | 33 | 39 | 45 | 51 |
| 5 | 25 | 35 | 45 | 55 | 65 | 75 | 85 | |
| X[7] | 49 | X[63] | 77 | 91 | 105 | 119 | ||
| 9 | 81 | 99 | 117 | 135 | 153 | |||
| 11 | 121 | 143 | 165 | 187 | ||||
| 13 | 169 | 195 | 221 | |||||
| X[15] | 225 | X[255] |
Die ab 15 beruhen auf der zweiten binomischen Form:
(2^n+1)*(2^n-1) = 4^n-1=2^(2*n)-1
Dies führt zu weiteren Spontanen Ausnahmen, wenn eine der beiden Zahlen nicht
prim ist.
Allemal läßt sich obige Formel von rechts nach links anwenden:
15 * 17 = 3 * (5 * 17) = 3 * 85 = 5 * (3 * 17) = 5 * 51.
Wir wissen (noch) nicht, ob derartige Umformungen die einzigen weiteren
Lösungen sind, -- sie sind allemal weit außerhalb des für
das CWN-Notationsproblem relevanten Bereiches.
Je nachdem wie die Zahlen verwendet werden, bewirken sie entweder, dass e-schreibbare Kinder e-schreibbar bleiben (kleinere Zahl als K-Dauer, größere als Faktor), oder sogar, ganz paradox zu unserem Grundproblem, dass nicht-e-schreibbare K-Dauern im Transformations-Result "plötzlich" e-schreibbar werden (kleiner Zahl als Faktor, größere Zahl als K-Dauer), siehe die folgenden Beispiele.
Grundsätzlich findet der metricSplit-Algorithmus auch all diese Spontanen Ausnahmen und wendet die Transformationen in entsprechend weiterem Rahmen durchaus an.

Es folgen einige signifikante Beispiele für die unterschiedlichen Kombinationen von E-Schreibbarkeit vor und nach der Anwendung von Transformationen. Vereinfachend gilt, wie erwähnt, dass diese nur von K-Dauer und Faktor abhängt. Deshalb gelten die folgenden Beispiele und Bedingungen für Geschwister-Verschmelzung entsprechend auch für Synkopen und Hemiolen, solange der Faktor derselbe ist. Einer eigenen Diskussion bedürfen folglich nur die Punktierung und die Fünfer(5)-Synkope.
Die Dauer der Knoten der zweiten Ebene (der Kinder der Wurzel)
im 18/16-Metrum 2*3*3*1/16 beträgt 9/16 und ist nicht
e-schreibbar, jedoch die ihrer Kinder (3/16), und der Zusammenfassung von zweien(2)
davon (6/16=3/8).
Zwischen der Kind-Darstellung in Zeile "C" und
der Freien Zerlegung in Zeile "F" könnte durch einen einzuführenden
Stilparameter entschieden
werden.
Normalerweise aber sollte die "C" Lösung bevorzugt werden, da darauf wiederum
eine zumindest teilweise Zusammenfassung sinnvoll anwendbar ist, siehe Zeile "C+",
wegen e-schreibbarer Kinder und Faktor=2.
Die Darstellung "X" ist zu verwerfen und würde von unserem Algorithmus auch nie
gefunden werden, obwohl sie rein arithmetisch möglich wäre:

Umgekehrt beim 15/16-Metrum 3*5*1/16: Hier ist der
Elterknoten e-schreibbar, nicht jedoch die Kinder,
und auch nicht die Verschmelzung zweier Geschwister.
Die E-Schreibbarkeit ist "Spontane Ausnahme", siehe obige
Multiplikationstabelle, denn die Schreibweise mit drei Verlängerungspunkten war ja
ehedem für einen ganz anderen Kontext erfunden worden, nämlich für die feste
Kombination "15+1", genannt "dreifache Punktierung"!
Zeile S0 ist e-schreibbar wie in Zeile SX, verwirrt aber nur, da es sich um eine "falsche Synkope" handelt, und wird von unserem Algorithmus nicht errechnet. Die richtige Synkope in Zeile SY ist hingegen nicht e-schreibbar und wird deshalb ebenfalls nicht generiert.

Im verdoppelten Metrum 2*3*5/16 kann man o.e. Paradoxie bewundern: die e-schreibbare Dreiersynkope, obwohl der K-Knoten nicht g-schreibbar, noch nicht einmal e-schreibbar ist:

Dieselbe Gleichung "3*5=15" ermöglicht im Metrum x*5/16 (also mit zwei(2)-geteilten Kindknoten, warum auch immer ...) die direkte E-Schreibbarkeit des Resultat-Wertes von einfachen Punktierungen, siehe wieder obige Multiplikationstabelle:

Beim dualen 15/16-Metrum 5*3*1/16 sind hingegen beide Ebenen e-schreibbar.
Der Wurzel-Knoten wieder "spontanerweise".
Von den Zusammenfassungen sind nur die mit geradzahligen Faktoren e-schreibbar.
(Die freie Zerlegung KX ist übrigens durchaus diskussionswürdig, besser wäre wohl
die partielle Geschwister-Verschmelzung KG. SX statt S0 wird nicht empfohlen,
obwohl e-schreibbar, und wird von unserem Algorithmus auch nicht errechnet.)

Verdoppeln wir diesen Kontext zur Metrik 2*5*3*1/16, so ergibt sich die in obenstehender Tabelle erwähnte Spontane Ausnahme der e-schreibbaren Synkope in einer Fünfer-Metrik. Es ist allerdings fraglich, ob man die wirklich will:

Bei der Punktierungs-Transformation kommt eine Voraussetzung bzgl. der Art der Teilung der beteiligten Elterknoten hinzu: äquidistant durch zwei(2). Dies ist in Kombination mit einem ungeraden Nenner (!=2^x) nur in zusammengesetzten Metriken anzutreffen, bei denen eine Art von Tempo-Relation durch die Schreibweise mit verschiedenen Grunddauern ausgedrückt wird.
So sind z.B. im Metrum 4/8+5/8 in beiden Hälften alle Ebenen stets äquidistant zwei(2)geteilt (es heißt ja NICHT 4/8+5/8(5)!), aber die Ereignisse der zweiten Takthälfte halt "leicht langsamer" als die der ersten:
Die Schreibweise mittels Proportion sollte bei einer Einführung von "Abkürzenden Proportionen", wie oben diskutiert, von unserem Algorithmus dann gefunden werden, wenn sie das Ergebnis einer Punktierungs-Zusammenfassung e-schreibbar macht, also Zeile PP stattt PX, nicht aber ohne dies, wie in Zeilen P und PC.

Ein wesentlich häufigeres Phänomen allerdings ist die Duole, also die Zweiteilung anstelle der Dreiteilung, wie im Metrum 2*3*1/8+2*2*3/16. Diese kann ja als ein duales Phänomen zu der sehr häufigen Triole gesehen werden. Hier kann jedoch mittels eines Stilparameters die Proportionen-Schreibweise grundsätzlich bevorzugt werden (Zeile D), Allemal aber sollte diese Schreibweise automatisch gewählt werden, um das Ergebnis von Punktierungen aller Ebenen e-schreibbar zu machen (Zeilen P4, P8, P16):

Folgendes Beispiel (im Metrum 2*2*3*1/16)
zeigt o.e. Problem, dass durch die Einführung einer
"Abkürzenden" Proportion ein Nenner zur E-Schreibbar-Machung eines
Transformationsergebnisses ("Punktierung") zunächst vereinfacht wird, er aber auf
tieferer Gliederungsebene doch wieder in seiner komplexeren Form auftritt,
was die Einführung einer zweiten, die erste ausgleichenden Proportion nötig macht.
Es zeigt sich hier wieder das Problem des "Aufschaukelns" der Proportionen,
wie schon
im Vorgängerartikel diskutiert
,
da die Achteltriole der letzten Zeile
sich "natürlicher" liest in Verbindung mit der vorangehenden
punktierten Halben, aber der Ausgangs-Schreibweise deutlich widerspricht:

Die größer-zahligen der Spontanen Ausnahmen (siehe obige Multiplikationsmatrix) spielen praktisch wohl keine Rolle: Zunächst ist die doppelte Punktierung e-schreibbar, wenn die Grunddauer neun(9) beträgt, wegen 7*9=63=64-1.

Weiterhin sind alle Faktoren 2^n anwendbar (für Hemiolen, Geschwister, etc.) wenn
die Grunddauer als ungeraden Anteil genau 2^n-1 enthält, also sieben(7) oder gar
fünfzehn(15=3*5). Aus historischer Sicht ist dies wiederum der oben erwähnte
"Missbrauch" der Punktierung, wird aber von metricSplit durchaus gefunden und
für systematisch erachtet.
(Ganz unabhängig davon gibt es allerdings einen Stilparameter boolean
syncope_longer_4, um die Fünfer-Synkopen wegen Ergonomischer Zweckmäßigkeit
grundsätzlich auszuschalten.)

Wie bei allen Teil-Projekte, die in unsere gemeinsame Musik-Software BandM Models of Music einfließen, gebührt besonderer Dank für fruchtbare Diskussionen von Theorie und Praxis meinem Kollegen Baltasar Trancon y Widemann.
1 Wofür es ja in der Mehrzahl der Stile und Notationsweisen auch keinerlei Notwendigkeit gibt: Eine ungetrennte Folge von mehr als einer Pause ist identisch mit einer Pause von der Dauer der Summe derer Dauern. Andererseits setzt der Verfasser auch in ganz "konventionellen" Kontexten manchmal einen Betonungs-Keil auf eine Pause, was bedeuten soll "betont pausieren", oder "Klang-Ende scharf konturieren". Wenn auch eine Pause nach einer Pause derartige Attribute tragen könnte, gilt diese Gleichung nicht mehr!
2 Es mag fast scheinen dass das Finale von op. 111 von Beethoven genau diese Unendlichkeit re-definieren will, als ebenso unbegrenzt fortsetzbar, aber nicht mehr als Zwei- sondern nun als Drei-Teilung, als eine "perfekte".
3 Dies ist deshalb unproblematisch, weil in den meisten praktisch/historisch tatsächlich auftretenden Fällen diese Gestalten zusätzlich durch Kleinstich hervorgehoben und so explizit als aus dem metrischen Kontext herausgenommen gekennzeichnet werden.
4
Es sind andere Regelsystem denkbar, die auch ihre Vorteile haben, z.B.
statt diesen Abschnitt, Liste 2, Listenpunkt 4:
"Die Differenz aus einer expliziten Dauer des Elterknotens und
der Summe aller Kindknoten MIT einer Dauernangabe muss positiv sein und
wird auf alle Kindknoten OHNE eine Dauernangabe gleichmäßig aufgeteilt."
Aber da derartige Regeln ja auch dazu dienen, Flüchtigkeitsfehler zu
entdecken, ist eine gewisse Partialität durchaus ergonomisch gewünscht.
5 ...oder wenn er weitere Information in Form von beigefügten Parameterwerten trägt, z.B. Lautstärkeänderungen oder Spielvorschriften. Von derartigen problematischen Mischformen der Notation wird, wie oben erwähnt, im gesamten Artikel abgesehen!
6 Diese Art der Vordergrund-Schreibweise ist u.E. die einzige mathematisch konsistente und auch psychologisch zweckmäßige. Leider sind in der Praxis viele abweichende und ungeeignete Versuche der Notation verbreitet, siehe die ausführliche Diskussion im Vorgängerartikel.
7 An den Rändern gilt das in der Praxis nicht, da es z.B. in den meisten modernen Zeichensätzen kein Grundsymbol kürzer als die 128tel-Note gibt, oder nichts länger die "Brevis". Das bedeutet aber keine prinzipielle Grenze, und davon wird im folgenden abstrahiert.
8 Normalerweise treten dann mindestens zwei (>=2) der Kindknoten notationell in Erscheinung, man beachte aber die möglichen Konsequenzen von Stilparameter merge_may_cross_bracket_limit==true, s. Abschnitt 2.15.1.
9 In der Tat würde schon 3*(1/4) reichen, um SM-48 und SM-84 auszuschließen, da Phase zwei/Div ja nur unterhalb der explizit angegebenen Blätter des MTS arbeitet, siehe Abschnitt 2.13. Das ändert jedoch nichts am prinzipiellen Problem, wie es bei MTS=1/1 auch aktuell wird.
10 Höherzahlige Teilungen sind Chopinesque, haben also nur eine flache Hierarchie, und alle Knoten sind Geschwister. Die Knoten dieser oberste Teilungsebene können allerdings ihrerseits zweigeteilt sein, das heißt unter ihnen können Synkopen und Punktierungen durchaus auftreten, -- wieder ein Beispiel für Kompositionalität.
11
Pausen unterhalb der Zählzeit werden in neuerer Praxis allerdings auch synkopiert,
z.B. nach dem Muster
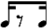
[[Dies ist zur Zeit noch nicht implementiert.]]
12 Genau genommen kann die Information "isFirst" am Wechsel der Ereignisnummer erkannt werden, und "isLast" an einem parallelen Aufaddieren der Dauern. Aber da beides im Visitor schon bekannt ist, wäre das recht uneffektiv.
©
senzatempo.de
markuslepper.eu
2019-12-20_20h54


produced with
eu.bandm.metatools.d2d
and XSLT
music typesetting by musixTeX
and LilyPond