
| zu den Gesamtinhaltsverzeichnissen |
| ^inh 2012102700 | phaenomen |
1
Einleitung
1.1
Kontext dieser Arbeit
1.2
Die Wichtigkeit des "Mittelgrundes"
1.3
Problemstellung
2
Struktur der metrischen Notation
2.1
Entstehung der Notenwerte in der Mensuralnotation
2.2
Der Takt als Zusammenfassung von Aktionen
2.3
Die historische Herkunft der Grunddauernwerte
2.4
Metrik als Zusammenfassung von Grundschlägen
2.5
Die drei Organisationsbereiche der metrischen Notation
2.6
Verschiebung der Grenzen der Organisationsbereiche
2.7
Die "mentale Einfachheit" von Empfindungsfolgen
2.8
Die innere Hierarchie eines Taktes
2.9
Weitergehende Komplizierung der metrischen Raster
2.10
Umrechnung in Taktbezeichnungen
2.11
Interpretation von konventionellen Taktart-Angaben z/n
2.11.1
Konventionelle Bedeutung der Taktbezeichnungen aus 2^a*3^b
2.11.2
Primfaktoren größer drei und additiv begründete Zähler
2.12
Wechselnde Metren
3
Dauern im Kontext metrischer Notation
3.1
Dauern und ihre Darstellung
3.1.1
Auswirkungen der n-olen im Mittelgrund
3.1.2
Mehrdeutigkeiten der Vordergrund-Repräsentation von n-olen
3.1.3
Kompliziertere n-olen
3.1.4
Verselbständigte n-olen
3.2
Algorithmen zur metrisch korrekten Notation von Rhythmen
3.3
Die gewichtsbasierten Algorithmen
3.4
Balkengruppen in lilypond
3.5
Nur nicht-lokal lösbare Probleme
3.6
Unser Vorhaben eines graphbasierten Algorithmus'
4
Bibliographie
Das tScore-Projekt, vorangetrieben im Rahmen der BandM-Musik-Software
[bandmMusic] , ist ein Forschungs- und Entwicklungsvorhaben
einer Mensch-Maschine-Schnittstellensprache zur adäquaten Denotation
beliebiger zeitbezogener Ereignisfolgen.
Es beinhaltet als einen kleinen Teilbereich die
Generierung von visueller Notenausgabe durch Ansteuern von Notensatz-Software wie
lilypond [lilyPond] oder musix-TeX [musixtex].
Ein wichtiger Schritt dabei ist die Umsetzung abstrakt gegebener
Dauernfolgen, wie sie von tScore ja in prinzipiell beliebiger Codierung
erzeugt und verarbeitet werden können, in Folgen von rhythmischen Werten
der musikalischen Notenschrift.
Diese Übersetzung kann nun mitnichten "lokal" und "eins-zu-eins" erfolgen,
sondern muss vielmehr einem sogenannten Metrum entsprechen, welches im
System konventioneller musikalischer Notierung stets vorher ausgewählt werden
muss, um dann der gewünschten Notendarstellung zu Grunde zu liegen.
Die Aufgabe dieser Übersetzung ist mitnichten trivial, und
überraschenderweise in der wissenschaftlichen Literatur
offensichtlich weitgehend unbearbeitet.
Zu dem wenigen, in dem sie zumindest als eine unter vielen
behandelt wird, gehört die Dissertation
"Code-basierte Generierung interaktiver Notengraphik"
von Martin Gieseking, [gieseking] , die auch in anderen
Kontexten schon Berücksichtigung fand, z.B. wegen ihres
sehr nützlichen einführenden Teiles (siehe
senza tempo 20120701 00
und
20120822 00 )
Die Hauptteile dieser Arbeit bilden Ausführungen zu algorithmischen
Lösungen folgender Notationsprobleme: (a) der korrekten Notation von
Rhythmen bei gegebenem Metrum, (b) der horizontalen
Positionierung von Akkordgruppen und ihren Bestandteilen, und (c)
der graphischen Konstruktion von Balken und Bindebögen.
Die Ausführungen zu (a) sind es, die hier interessieren, und diese
gehen dabei zurück auf Teile der Dissertation
Music Notation by Computer
von Donald Alvin Byrd aus dem Jahren 1984, [byrd] .
Beide Autoren entwickeln einen Algorithmus, den wir im folgenden als gewichtsbasiert bezeichnen, da er eine lineare Abbildung von taktrelativen Zeitpunkten zu metrischen Gewichten zur Grundlage aller Entscheidungen macht.
Im Gegensatz dazu planen wir für tscore einen Algorithmus mit deutlich breiterem Anwendungsgebiet zu definieren, der z.B. die von beiden Autoren geforderten "lokalen Metren" behandeln kann, und der graphbasiert sein wird, also grundlegend anders aufgebaut. Dennoch ist eine ausführlichere Analyse der gewichtsbasiereten Algorithmen, ihrer Ziele, Ergebnisse und Prämissen, sehr gewinnbringend, und bildet mit Abschnitt 3.3 den eigentlichen Zielpunkt dieser Arbeit.
Außerdem werden die Ansätze in der lilypond-software besprochen, Abschnitt 3.4, wo zwar keine automatische Dauernübersetzung stattfindet, aber Bebalkung automatisiert und sehr weitgehend parametrisierbar ist.
Der Hauptteil dieser Arbeit jedoch ist eine grundlegende und umfassende Darstellung des Problems selbst, für Musiker und Nicht-Musiker geeignet, da wir feststellen mussten, dass selbst über die grundlegenden Strukturen und Begrifflichkeiten zwar diffuses Vor-Wissen und praktische Erfahrung weit verbreitet ist, aber eine exakte Diskussion und Begriffsklärung kaum je stattgefunden hat.
Beide Beiträge, der ursprüngliche Ansatz von Byrd, und seine Adaption durch Gieseking, haben große Verdienste, aber auch natürlicherweise enge Grenzen, da sie nur einen Teil der jeweiligen Gesamtarbeit ausmachen.
Die verschiedenen bei beiden Autoren auftretenden und unterschiedlich stark störenden Unzulänglichkeiten lassen sich vielfach auf einen Kardinalfehler zurückführen, der allerorten in der musikwissenschaftlichen und besonders musiktheoretischen Literatur anzutreffen ist, und den es deutlich aufzuweisen und zu vermeiden gilt, nämlich auf die Verwechslung von Vordergrund und Mittelgrund.
Unter "Mittelgrund" verstehen wir dabei Begriffsnetzwerke, Strukturen, Regeln, Logiken, Materialien, die sich zwar oft, aber eben nicht immer, in Notationen des "Vordergrundes" ausdrücken, fixieren und vermitteln lassen, aber nicht nur mit diesen nicht zusammenfallen, sondern vielmehr wesensmäßig auf ewig und inkommensurabel von ihnen getrennt sind.
So ist z.B. die Menge aller rationalen Zahlen ein mögliches "Mittelgrund"-Modell
von musikalischen Dauern. Dies steht zu der Menge
von graphischen Bestandteilen von Notenzeichen, welche in Musikniederschriften
Dauern bedeuten, zwar durchaus in Beziehung,
ist aber offensichtlich mit dieser keinesfalls wesensgleich.
Wem diese Unterscheidung haarspalterisch vorkommt, sei versichert, dass sie
in der Informatik, ja, in aller reflektierend arbeitender
Mathematik (z.B. Darstellungstheorie, Modelltheorie, Logik) unbebstrittene
Arbeitsgrundlage ist.
Die wohlbekannte und ubiquitäre
Unterscheidung zwischen "Syntax" und "Semantik" beim Entwurf einer
Computersprache kann durchaus als Beispiel von Vorder- und Mittelgrund
verstanden werden.
Hat man dies einmal akzeptiert, beachte man weiterhin, dass die Abbildungen zwischen
Vordergrund, z.B. Notation, und Mittelgrund weder rechts- noch links-eindeutig
noch -vollständig sein müssen. Die Beziehung zwischen beiden ist vielmehr
äußerst kritisch und kritikwürdig, im Sinne von "Kritik" als
notwendiger vorangehender wissenschaftlicher Analyse.
Die meisten Fehler, aber auch Mißverständnisse, im musiktheoretischen Diskurs
enstehen u.E. aus der Verwechslung dieser beiden Bereiche und der fehlenden
Problematisierung der zwischen ihnen vermittelnden Übersetzungsfunktionen.
1
Wichtig ist weiterhin, dass der Mittelgrund immer nur Modelle beinhaltet, die für bestimmte Zwecke konstruiert werden und für nur für diese, oder für diese und wenige ausgewählte andere, dann auch verwendbar sind. Ein auf den Vordergrund einer bestimmten Notationsweise bezogenenes Mittelgrundmodell kann z.B. psycho-interne Prozesse des Musiker in einer Konzertsituation abbilden wollen, ein anderes die Raumaufteilung der Notenzeilen nach druck-ästhetischen Kriterien und eingebautem Rauschen, ein drittes die harmonischen Prozesse nachbilden, zwecks möglichst einfacher Vergleichbarkeit. Offensichtlich fundamental verschiedene "Lesungen" derselben Vordergrundgestalt. Bei jedem Modell ist folglich explizit zu fragen, was es kann und was nicht.
Zuletzt sei noch empfohlen derartige Mittelgrund-Modelle möglichst mit mathematischen Methoden zu bauen. Diese erlauben die Verwendung wohlerforschter Standardverfahren, ohne dass man das Rad stets neu erfinden muss.
Um also im folgenden nicht nur über Notation als Vordergrundphänomen zu reden, oder den Mittelgrund implizit und verwaschen mitdenken zu müssen oder mit dem Vordergrund zu verwechseln, konstruieren wir also als dessen wichtigstem Bestandteil zunächst explizit ein mathematisches Modell von Metrik.
Um dazu den Zugang zu erleichtern geht dem wiederum voraus eine kurze Schilderung der historischen Entwicklung, da diese, wegen der Spuren, die sie in Strukturen, Benennungen und Schreibweisen hinterlassen hat, den unvorbereiteten Leser duchaus geeignet ist zu verwirren.
Nach einer kurzen Vorstellung des Problems als solchem wird zunächst der Kontext der Fragestellung genauer entwickelt. Zu bestimmen Einzelfragen, die hier nicht in aller Ausführlichkeit behandelt werden können, werden wir auf unsere Übersichtsarbeit senza tempo 2012070100 --- Synopsis of Musical Notation Encyclopedias zurückverweisen, resp. auf die dort vorgestellten Arbeiten, und auch direkt in das dortige Literaturverzeichnis linken.
Das Problem ist eines im Rahmen der taktbasierten Notation, auch genannt metrische Notation, wie sie sich im siebzehnten Jahrhundert aus der Mensuralnotation entwickelte, bis heute weiterentwickelt wurde, und bis heute verwendet wird. Sie wird auch genannt "CWN", "common Western notation" oder "conventional Western notation".
Die Problemstellung besteht darin, dass eine Folge von musikalischen Dauernwerten je nach ihrer Position im Takt unterschiedlich notiert werden soll. Dies, um die verschiedenen Gliederungsebenen der metrischen Hierarchie, die sehr verwickelt werden können, durch die Wahl der Notation möglichst deutlich werden zu lassen, um bequemes Lesen zu ermöglichen, z.B. fürs prima-vista-Spiel.
Es ist in mehrfacher Hinsicht wünschenswert, diese Entscheidungen als mathematische Funktion exakt zu notieren. So z.B. zum Zwecke der Algorithmisierung und automatischen Ausführung durch einen Rechner, aber auch um vergleichende Diskussionen auf eine exaktere Grundlage zu stellen.
Bei diesem Versuch stößt man schnell auf grundlegende Probleme:
Erstens ist die fundamentale Strategie für diese Entscheidungen mit Epoche, Stil und Genre durchaus variabel: Manches, was für Brahms-sche Kammermusik möglich ist, ist bei Militärorchester zumindest ungewöhnlich, was für ein Barockes Menuett ausreicht, reicht nicht für eine Jazz-Big-Band, etc. Die Funktionsdefinitionen müssen also entsprechend parametrisierbar sein.
Zweitens ist das metrische System der CWN selbst historisch gewachsen. Zwar wird es innerhalb je eines dieser sehr verschiedenartigen Verwendungsgebiete meist hinreichend konsistent verwendet. Aber auch derartig eingeschränkt ist es weder durch systematische Ableitung entstanden noch restlos systematisch definierbar.
Drittens gilt das verstärkt auch von der "Vordergrundgestalt" der Notation: Selbst wenn die möglichen Mittelgrund-Strukturen (so z.B. metrische Hierarchien, Taktarten, n-olen) systematisch erzeugbar sind, so existieren dennoch nicht für alle davon überhaupt Entsprechungen in der Vordergrundgestalt, also Zeichen, um sie aufzuschreiben.
Viertens durchdringen sich im Feld der Notation sehr unterschiedliche Bereiche mit nur teilweise relierten, ja, teils gar entgegengesetzten Tendenzen:
Wir werden versuchen, all diese Aspekte, soweit sie für die Grundfrage relevant sind, gebührend zu behandeln und möglichst säuberlich zu scheiden.
Der nächste Abschnitt bringt zunächst eine sehr vereinfachte Darstellung der historischen Grundlagen der metrischen Notation, soweit diese für die Klärung dieser Teilprobleme relevant sind.
Eine vollständige Lösung des Hauptproblems, der algorithmischen
Berechnung von korrekter Notation von Rhythmen bezogen auf
eine gegebene metrische Struktur,
scheint aus den genannten
Gründen weder möglich noch sinnvollerweise anzustreben.
Wir verweisen auf [byrd] , wo derartige Ambitionen mit gleichermaßen
überzeugender wie kurzweiliger Argumentation ausführlich zurückgewiesen werden.
Ein mathematischer Ansatz kann aber
durchaus weiter gehen als das in [gieseking] als "Stand der Technik"
dargestellte
Insbesondere sollten die Möglichkeiten von Parametrisierung,
punktuellen Lizenzen und Nach-Bearbeitung in systematischer
Weise erforscht und dargestellt werden.
Zu all diesen Zwecken entwerfen wir nun, wie angekündigt, erst einmal ein
Modell der Mittelgrundstruktur von musikalischer Metrik.
Die Vorläufer-Notation der metrischen Notation war die "Mensural-Notation". Wir geben hier eine sehr stark vereinfachte Darstellung, die lediglich ausreichen soll, den historischen Kontext und seine Konsequenzen für die CWN zu erläutern. Die sich über Jahrhunderte hinziehende Entwicklung dieser Notation wird eingedampft auf ihre Grundprinzipien. Für eine gute Einführung siehe [mggprisma] .
Die Mensural-Notation kannte die Teilung der Zeit auf verschiedenen Ebenen, die hierarchisch übereinandergeschichtet sind. Prinzipiell kann jede Note einer bestimmten Ebene in zwei(2) oder in drei(3) gleichlange Noten der nächst tieferen, also nächst schnelleren Ebene unterteilt werden. Diese Teilungsart wird je Teilungsebene zu Beginn des Werkes festgelegt und gilt grundsätzlich gleichermaßen für alle Noten dieser Ebene (abgesehen von punktuellen, explizit zu notierenden Ausnahmen). Die Teilung durch drei heißt perfectum, die durch zwei(2) imperfectum. Die Teilungsebenen hießen z.B. (in den meisten historischen Ausprägungen) "modus", "tempus", "prolatio", so dass beliebige Kombination der Unterteilungshierarchie definierbar waren, wie "modus perfectus, tempus imperfectum, prolatio perfecta", als Teilungsfolge 3-2-3 der "longa" genannten Note. Diese Hierarchie von Teilungen wird zu Beginn des Werkes angegeben. So bestimmt sie die Ausführung der verschiedenen Notenlänge und die Verhältnisse der verschiedenen Teilungsebenen. (Daneben können ad-hoc "Proportionen" auftreten, die diese Grundteilung für kurze Zeit modifizieren, oder es kann auch innerhalb eines Satzes dauerhaft von einer Teilungsart in eine andere gewechselt werden.)
Diese Notation wurde bis zum siebzehnten Jahrhundert verwendet für geistliche Kompositionen, die (meist ohne Instrumentalbegleitung) von hochspezialisierten Sängern aufgeführt wurden. Zu deren Ausbildung gehörte u.a. das korrekte Teilen der Dauern auf den verschiedenen Notationsebenen, nur nach Zeitgefühl und prima vista. Die dabei hervorzubringenden Rhythmen konnten (besonders unter Verwendung o.e. "Proportionen") in der Spät- und Niedergangszeit dieser Kultur (sog. "manierierte Notation") ein Maß an Komplexität erreichen, welches selbst heutigen Rhythmus-Spezialisten und professionellen Neue-Musik-Schlagzeugern Angst und Ehrfurcht einflößt.
Bei all dieser Artistik, bei Notation, Systematisierung und philosophischem Überbau, ging es aber allemal um Gesang und um divisive Prozesse.
Takt hingegen ist etwas ganz anderes, ja, fast als "Gegenteil" auffassbar!
Der Takt kommt bestenfalls aus dem Tanz, schlimmstens aus dem Marsch, allemal aus der Bewegung, und besteht darin, dass eine Folge von (fast immer fast gleich-langen) sich wiederholenden Grund-Einheiten, sog. "Schläge" / "Zählzeiten" / "beats", zu einer Einheit zusammengefaßt werden, eben dem "Takt" / "measure". Diese Schläge werden dann innerhalb dieses Taktes als "erste Zählzeit", "zweite Zählzeit", etc. durchnummeriert, und verkürzend bezeichnet wie "die Eins von Takt 16".
Ein gesamtes Musikwerk wird dann aufgefasst und notiert als eine Folge von gleichartig strukturierten derartigen Takten.
Wichtig ist, dass allen diesen Komponenten, der Zählzeit, dem Takt und dem Vorgang der Gruppenbildung, konkrete mentale Mechanismen beim Musizieren entsprechen: Die Zählzeiten werden empfunden und die gespielten Ereignisse relativ zu diesen Empfindungen ausgelöst; die Takte werden durch vor-bewußtes unterschiedliches "mentales Einfärben" der Zählzeiten wirksam; oberhalb der Takt-Ebene orientiert man sich durch Lenken der Augen auf die geschriebenen Noten, oder durch nun bewußtes Zählen, etc.
Die Taktbasierung der CWN hat also gleichermaßen philosophische und mathematische, aber auch musikantisch-praktische Aspekte, die wir im folgenden alle sowohl zu berücksichtigen als auch zu scheiden versuchen.
Die einfachste Verdeutlichung ist ein einfaches Tanz-Schema, wo jeder Schlag einem Schritt entspricht, und die an derselben takt-relativen Position stehenden Schritte gleich ausgeführt werden, also von Takt zu Takt gleich sind, aber innerhalb des Taktes verschieden:
Takt 1 | 2 | 3
Zählzeit 1 2 3 | 1 2 3 | 1 2 3
_________________ ________________ ________________
/ \ / \ /
Aktionen: A | A | A
B | B | B
\_________|______/ \__________|______/ \___________
C | C | C
\____|____________/ \____|____________/ \_______
| |
|
Diese Funktionsunterschiede der Zählzeiten gibt es ähnlich auch schon in der oben beschriebenen Mensuralnotation und ihrer Musik, als auf ausgewählten Ebenen der Teilung die "schwere" und die "schwache" Zeit unterschieden wurde, und bestimmte harmonische Ereignisse beim Komponieren nach diesen Kategorien verteilt werden mussten.
Bei der metrischen Notation hingegen werden die Funktionsunterschiede besonders für die Ausführung wichtig: Die einzelnen Zählzeiten bekommen sehr feine, aber durchaus unterschiedliche Unterschiede in den Lautstärken, und auch ihre Dauer und Tonform wird in den meisten musikalischen Stilen auf sehr subtile, aber wirksame Weise je Zählzeit modifiziert. So werden z.B: die Ereignisse, die auf Zählzeiten fallen, etwas stärker betont, und unter diesen wiederum die, die auf die ersten Zählzeiten der internen hierarchischen Gruppen fallen, (s.u. das konkrete Beispiel in Abschnitt 2.7).
Diese Einfärbungen der Zählzeiten wiederholen sich grundsätzlich mit jedem Takt. Die konkreten Ausführungen dieser Einfärbungen werden als Teil der Agogik bezeichnet; ein davon abstrahiertes theoretisches Modell nennt man metrische Gewichtung oder metrisches Raster oder metrisches Schema.
Die konkret gespielten Rhythmen "verhalten sich zu" diesem, oder gar "gegen dieses" metrische Raster. Zumeist stehen die konkrete erklingenden Ereignisse nicht auf den gedachten Zeitpunkten der Zählzeiten, sondern dazwischen, und oft erklingt garkein neuer Anschlag auf einer Zählzeit. Die Struktur des Erklingenden kann sich im Verlaufe eines Werkes vom metrischen Schema entfernen und sich ihm wieder annähern. (Genau dies verursacht ja erst das Grundproblem dieser Untersuchung !-) Das metrische Schema färbt aber allemal die Ausführung und Empfindung der notierten Ryhthmen, wenn auch in unterschiedlicher Weise und verschiedenem Grad, je nach gerade erklingendem Rhythmus und nach dem "gelernten" Kontext vorangehender Takte.
Wichtig ist in unserem Zusammenhang, dass der musikalische Denk- und Produktionsvorgang bei der Taktbildung ein additiver ist: Ereignisdauern (und damit Notenwerte) werden zum Takt zwecks Gruppierung zusammengefasst. Dies zeigt sich deutlich bei Taktarten von schnelleren Volkstänzen, die Zählzeiten in ungleichen Gruppen zusammenfassen, wie "zwei-plus-zwei-plus-drei", was nicht mehr rein durch Division abgeleitet werden könnte.
Ein erstes Verständnisproblem der CWN besteht nun in der Auswahl und Benennung der für Dauernwerte verwendeten Grundzeichen. Dieses Problem ist ein rein theoretisches, notationstechnisches, und ist darin begründet, dass (naturgemäßer- und zweckmäßigerweise) im Laufe der historischen Entwicklung die mit dem divisiven Denken der Mensuralnotation entwickelten Notensymbole beibehalten wurden und benutzt, um schrittweise die neue, tatkbasierte, additive Notation zu konstruieren. 2 Es ist aber durchaus geeignet, den Leser zunächst zu verwirren, und soll deshalb hier kurz angesprochen werden. Aussderdem ist es ein anschauliches Beispiel, wie mathematische Mittelgrund-Modelle und historische Vordergrund-Entwicklung auseinanderfallen können.
Der historische Prozess war, stark vereinfacht, folgender:
Meist wurde, weil sie so praktisch zu schreiben ist,
die Note "Semi-Minima" gewählt, um einen(1) Grundschlag darzustellen.
Meist wurden 4(vier) dieser Grundschläge
für einen Takt benötigt, der in diesem Fall (aber in keinem andern!)
die Länge der "Semi-Brevis" bekommt, im Sinne von zwei "imperfekten" Teilungsebenen.
Demzufolge wurde die "Semi-Brevis" als "Ganze" / "Ganze Note" bezeichnet,
nämlich als "die, die einen ganzen Takt dauert".
Die Zählzeit in erwähntem Falle,
das Notensymbol der Semi-Mminima, nennt man folglich "Viertel",
da nämlich vier(4) von ihnen dem "ganzen Takt" entsprechen,
also der Dauer der "Ganzen Note".
Die Wortbezeichnungen "Ganze" und "Viertel" als Dauernangaben wurden nun aus diesem Zusammenhang abstrahiert und eingefroren, und geben immer, in jedem Taktzusammenhang, korrekt die gegenseitige Längen- oder Dauern-Proportion dieser beiden Notensymbole wieder. Als Wortbildung jedoch (warum die "Ganze" so heißt, etc.) sind sie aus obiger Anwendungssituation zustandegekommen, die nur als "zufällig" bezeichnet werden kann. Die "ganzen Takte" der meisten heute üblichen Taktarten dauern mitnichten eine "Ganze" / "Ganze Note"!
Dieser (zunächst rein historische) Widerspruch wird offen sichtbar
(wird gleichsam "materiell")
in vielen Regelwerken zur Notenschrift, welche für Pausen,
die einen "ganzen" Takt dauern, das Symbol der "ganzen Pause" vorschreiben
(das ja im Sinne des nächsten Absatzes
der Länge 1/1 entspricht), auch in allen Fällen wo die Taktlänge
kürzer ist [wanske, , S. 65 und 123].
Diese Pause wird darüberhinaus, anders
als alle anderen, in die "geometrische" Mitte des Taktes geschrieben,
unabhängig von etwaigen Rhythmen in parallelen Stimmen und der durch
sie begründeten Raumverteilung.
(Diese nur historisch verständliche Sonderrolle der Ganz-Takt-Pause wird
allerdings in der zeitgenössischen
Notation mehr und mehr aufgegeben zugunsten der "normalen", dauernrichtigen und
vertikal "normal" ausgerichteten Schreibweise.)
Wenn man dies als "historische Diagonale" bereit ist zu ignoriern, ist das Benennungssystem dennoch sinnvoll: In der mathematischen Formulierung gibt man der Dauer der "Ganzen Note" den Zahlenwert "1", und kann alle abgeleiteten Dauern durch rationale Zahlen repräsentieren, die "Viertelnote", die alte "Semi-Minima", ist dann einfach die Dauer "1/4".
Die Benennung der Viertelnote ist also ebenso zufällig wie die der Ganzen.
Das divisive Prinzip der Mensuralnotation wird weiterhin übernommen, aber eingeschränkt auf die Teilung durch zwei(2). Die Grunddauern der CWN, also die, die ohne weitere notationelle Zusätze mit einem einzigen einfachen Zeichen darstellbar sind, ergeben sich durch fortgesetzte Teilung durch den Faktor zwei(2), ausgehend von der "Brevis", welche, da die "Semi-Brevis" ja zur "Ganzen" wurde, in der Repräsentation als rationale Zahl mit dem Wert "zwei(2)" dargestellt wird.
Als Grunddauern ergibt sich also eine Folge (meist negativer) Potenzen von zwei(2); nämlich 2=Brevis, 1=Ganze, 1/2=Halbe, 1/4=Viertel, 1/8=Achtel, 1/16=Sechzehntel, etc., normalerweise bis 1/128, siehe unten Abschnitt 3.1.
Wichtig ist, davon deutlich zu unterscheiden die Konstruktion metrischer Bezugssysteme. Diese läuft im einfachsten Falle ab wie folgt:
a) Eine der Grunddauern wird als Grundschlag ausgewählt, ...
b) ...und von diesem Grundschlag werden "n" Zählzeiten zu einem Takt
zusammengefasst.
(Diese Formulierung ist stark vereinfacht. Sie reicht aber zunächst für unsere grundlegenden Überlegungen. Sie wird in späteren Abschnitten weiter präzisiert werden, und später sogar grundlegend modifiziert.)
Der in a) ausgewählte Grundschlag ist meist die Viertelnote, aber auch Halbe, Achtel und Sechzehntel finden sich in der Literatur, in abnehmender Häufigkeit. Diese Wahl als solche sagt nicht sehr viel, folgt eher pragmatischen Gründen: Wenn viele weitere, feinere Unterteilungen des Schlages stattfinden sollen, ist es eben notationstechnisch zweckmäßig, einen längeren Notenwert für den Schlag zu wählen. Viel mehr als das, oder halt reine Gewohnheit, steckt meist nicht hinter dieser ersten Entscheidung!
Die genaue Art und Weise der Zusammenfassung zu b) kann sehr komplex werden, ist das eigentliche Feld unserer Analyse, und wird weiter unten genauer betrachtet, siehe Abschnitt 2.8.
Auf diese Weise werden Taktarten definiert,
die (in den meisten Fällen, aber nicht immer!) durch eine
Angabe bezeichnet werden, die einem mathematischen "Bruch"
ähnelt: Oben steht die Anzahl "n" der Zählzeiten, unten steht der Nenner des
Grundschlages.
Häufige Taktarten sind 4/4, 2/2, 3/4, 6/8,
es sind aber auch möglich 4/2, 2/1, 3/8, 5/4 und 7/16.
Man beachte, dass dies keine rationalen Zahlen sind, und keinesfalls "gekürzt"
werden dürfen: Die Taktart "6/8" ist etwas ganz anderes als "3/4".
Bei jeder gegebenen Taktart hat ein Takt eine bestimmte Taktlänge. Dies ist eine rationale Zahl, die sich aus dem Produkt der Länge des Grundschlages und dessen Anzahl je Takt ergibt. So haben 6/8-Takt und 3/4-Takt beide die Taktlänge 3/4.
Am Beginn jeden Werkes wird die Taktart angegeben. Innerhalb des Werkes können Taktwechsel vorkommen: Mit Ablauf eines Taktes kann für die folgenden Takte eine neue Taktart angegeben werden, die ab dann gilt, ggfls. bis zum nächsten Taktwechsel..
Jede notierte Stimme eines Werkes muss in jedem einzelnen Takt eine (ununterbrochene, nicht-überlappende) Folge von Ereignis-Symbolen (Spielereignisse oder Pausen) enthalten, so dass die Summe deren Dauernwerte gleich ist der Taktlänge der für diesen Takt gültigen Taktart (der "momentan gültigen" Taktart). 3 Der erste Takt eines Werkes kann kürzer sein als von der Taktart gefordert. Man nennt diesen einen "unvollständigen Takt" oder "Auftakt". In der Zählung der Takte wird er dann meistens nicht berücksichtigt. Im klassisch-romantischen Stile, wenn der Abstand zwischen ihnen nicht allzu groß ist, ist oft der allerletzte Takt des Satzes auch unvollständig und ergänzt sich mit dem allerersten zur geforderten Dauer.
Durch die Bindung eines Musikstückes an eine solche Taktart ergibt sich für seine zeitliche Struktur eine Hierarchie von drei(3) Bereichen der Zeit-Organisation:
Dies bedeutet allerdings eine Hierarchie von Hierarchien, denn jeder Organisationsbereich ist in sich wiederum hierarchisch gegliedert, da Dauernwerte "nach unten hin" in wohlunterschiedenen Schritten zunehmend unterteilt werden können, nach "oben hin" aber zu größeren Einheiten zusammengefasst.
Folgende Graphik soll diese Schichtung veranschaulichen:
Taktgruppen ("Groß-Metrik"/"Periodik")
| X | X
| |
| X | X | X
---------------------------------------------------------------------------------
Takt (6/4) | X | X | | |
| | | | |
| X X | X X | | |
| | | | |
Zählzeit | x x x x x x | x x x x x x | | |
---------------------------------------------------------------------------------
Rhythmus | x xx xxxx xxx x | x x x x x x| | |
| | xx xx xx | | |
|
Die Komplexität unseres Grundproblems (dem Metrum adäquaten Notation gegebener Dauernfolgen) ergibt sich daraus, dass in diesen drei Organisationsbereichen jeweils unterschiedliche Regeln herrschen, bezogen auf die rein mathematische Mittelgrunds-Struktur, bezogen auf die konkrete psychische Betätigung der beteiligten Menschen, bezogen auf die Vordergrundstruktur der notationellen Konventionen, bezogen auf die historische Herkunft der angewandten Mittel, etc.
Darüberhinaus können die Elemente dieser drei Organisationsbereiche durchaus in unterschiedlichen Verhältnissen zu einander stehen, abhängig von Stil, Genre, Epoche, etc.
Grundlegende Prinzipien sind die oben dargelegten:
Die für unser Thema wichtigsten Unterschiede der drei Organisationsbereiche sind
| Organisationsbereich | Notation | Ableitungsmethode | Zahlenbasis | Teilungsart |
| oberhalb Takt | (keine) | meist multiplikativ (oft subtraktiv!) | meist 2 | heterogen od. homogen |
| im Takt | explizit | meist multiplikativ, aber auch unsymmetrisch additiv möglich | 2 und 3 (4 und 5) | heterogen od. homogen |
| unterhalb Zählzeit | explizit | divisiv | 2 (alle anderen möglich, aber explizit zu verlangen) | nur homogen, "mechanistisch" |
Fest steht allein, dass der Organisationsbereich der Takt-Ebene der zentrale ist: Die Taktangabe ist allemal explizit, man orientiert sich im Werk, in dem man Takte zählt, und innerhalb des Taktes Zählzeiten. Diese entspricht bei der Hervorbringung im Gehirn des Musikers, wie bei der Rezeption im wippenden Fuß des Hörers, einem neuronalen Grundmechanismus. Ebenso der Takt, der als übergeordnetes Gewichtungs-Schema regelmäßig wiederkehrt und die grundlegende Orientierung erst ermöglicht.
Oberhalb der Takt-Ebene gibt es Gruppierungen von Takten, welche in bestimmten Stilen ("Klassische Periodenbildung") und bei manchen Komponisten ("Brucknersche Achttakter") von extremer Wichtigkeit sein können, aber auch ohne das allemal rezeptionspsychologisch zu beachten sind. Hier können einfache Zusammenfassungen auftreten, oder hierarchisch zusammengesetzte ("zwei Gruppen von dreimal vier Takten"). Erkenntnisse auf dieser Ebene gehen oft fließend über in das, was man oft "formale Analyse" nennt.
Interesanterweise sind hier oft (Mozart!) subtraktive Verfahren anzutreffen, nämlich innerhalb einer folge regulärer acht-taktiger Perioden solche die verkürzt sind und nur sieben oder sechs Takte dauern und auch deutlich als "Überraschung" gemeint sind.
Diese Ebene ist meist in der Notation garnicht präsent. Eine berühmte Ausnahme sind die expliziten, hinzugefügten textuellen Interpretationsanweisungen "RITMO DI TRE BATTUTE" / "RITMO DI QUATTRO BATTUTE" im Scherzo der Neunten Sinfonie, welche bestimmte metrische Gruppierungen der Takte fordern. Dies kann als Beispiel für eine "Grenzverschiebung" gesehen werden, siehe Abschnitt 2.6. Entspricht die Reaktion unseres Hörverstandes bei der Rezeption derart gruppierter sehr schneller Drei-Viertel-Takte hier nicht viel eher dem, was man als "9/4" oder "12/4" notieren müsste?
Unterhalb der Zählzeit kann diese weiter unterteilt werden, und das Ergebnis davon seinerseits geteilt, --- theoretisch unbegrenzt fortsetzbar. Die dafür nötigen Dauern-Zeichen und das Teilungsverfahren sind aus der Mensuralnotation übernommen, siehe oben Abschnitt 2.3 und weiter unten Abschnitt 3.1. Dabei ist die Standard-Unterteilung jeder Ebene stets die durch zwei(2). Jedoch gibt es Notationen, die diese Unterteilung ersetzen durch eine in "n" gleiche Werte, wobei n keine Zweierpotenz ist. Diese heissen "Triole" bei der Teilung durch drei statt durch zwei, "Quintole" durch fünf statt durch vier, etc.
In der Grundkonstellation haben die beiden Grenzen zwischen den drei
Organisationsbereichen genau definierte, unterschiedliche Funktionen.
Allerdings können sich diese Funktionen in bestimmten Situationen
durchaus verschieben.
Dies ändert nichts an den oben aufgezählten Prinzipien, jedoch an deren Relation
zur Vordergrundgestalt der Notation.
Nennen wir "mentale Zählzeit" die notierte Dauer, welche Musiker, Hörer und
Tänzer als Impuls empfinden, in der sie "zählen", und die nach obiger
Darstellung die psychisch-physiologische Grundlage der Taktdefinition ist.
Dann müsste im CWN-System, wenn diese Zählzeit ausschließlich (oder
zumindest überwiegend) in drei Teile geteilt werden soll, diese jedesmal
mit einer "Triolenklammer" versehen werden, da Teilungen durch drei
im Organisationsbereich unterhalb der Zählzeit nicht anders darstellbar sind
(s.u. Abschnitt 3.1).
Um diese umständliche Schreibweise zu vermeiden, wird dieser kürzere Notenwert
zum "Nenner" der Taktangabe gemacht, und der Faktor "drei" dem "Zähler" der
Taktangabe einmultipliziert. Es wird also die "notationelle Zählzeit" eine
Teilungsebene eine Ebene feiner
als die "mentale" gewählt, um die Triolenklammern zu sparen.
Als Konsequenz ist die Dauer der mentalen Zählzeit hier keine Grunddauer,
sondern eine "punktierte Dauer".
Ist der Takt im mentalen Sinne z.B. ein "Drei-Viertel-Takt", der konkret gespielte Rhythmus (im Organisationsbereich unterhalb der Zählzeit) würde aber fast immer die Teilung durch drei verlangen, dann ist es zweckmäßig, als notierten Takt einen "Neun-Achtel" zu wählen. Der mentale Grundschlag ist dann nicht die Achtel, sondern die "punktierte Viertel", die aus drei statt zwei Achteln besteht (s.u. Abschnitt 3.1), der nominelle Grundschlag ist die Achtel.
Das dies ein "gezielter Fehlgebrauch" ist wird besonders deutlich, wenn nur eine von mehreren Stimmen zum Zwecke einfacherer Notation die Taktart wechselt:

Umgekehrt kann auch die oberste Gliederungsschicht der eigentlich gemeinten Taktart aus dieser herausgenommen und stattdessen als "Gruppierung von Takten" notiert werden (Beethovens Neunte, Scherzo, wie oben erwähnt.) In extrem schnellem Tempo wird sogar der Takt als Ganzes zur mentalen Zählzeit, und die ursprünglich untere Grenze unseres Modelles wandert hoch, bis sie sich deckt mit der oberen! [gieseking, , S. 98], nennt das Scherzo aus Beethovens Fünfter Sinfonie als Prototyp.
Im Gegensatz zu der oben in Abschnitt 2.4 vorläufigerweise gewählten vereinfachten Formulierung "b) es werden n Zählzeiten zum Takt zusammengefasst" ist vielmehr festzustellen, dass innerhalb des Taktes, also im Organisationsbereich zwischen Zählzeit und Takt, in den meisten Fällen ebenfalls eine Hierarchie herrscht!
Diese Hierarchie ist, im Gegensatz zu denen der aussenliegenden Organisationsbereiche, naturgemäß in ihrer Höhe beschränkt und durch die Taktart festgelegt. Zumeist besteht sie aus zwei, oder gar nur aus einer Teilungsebene. Der unten erwähnten "24/16" mit seinen vier(4) Ebenen ist eine extrem hohe Ausprägung.
Nennen wir eine mental einfache Teilung eine jede, bei deren Hervorbringung der Musiker tatsächlich den Eindruck von n zwar unterschiedlich gewichteten, aber dennoch linear aufeinanderfolgenden und nur auf die jeweiligen Nachbarn bezogenen und eben nicht hierarchisch gegliederten Empfindungsereignissen hat.
Die Interpretation als eine solche mental einfache Teilung ist alternativlos nur bei den Teilungsfaktoren zwei(2) und drei(3).
Schon beim Faktor vier(4) hängt es von der konkreten Gestalt des musikalischen Materials, dem Tempo, der weiteren Unterteilung, etc. ab, ob hier vier gleichberechtigt linear folgende Punkte oder eine Gliederung von zwei-mal-zwei empfunden wird (vgl. oben die Graphik in Abschnitt 2.5, wo in den unteren Zeilen eine Vierer(4)-Gruppe einmal unmittelbar unter der Zählzeit angedeutet ist, ein andermal als zweistufige Zwei-Teilung!)
Nichtsdestotrotz ist es durchaus möglich sogar eine Folge und ein wiederkehrendes Metrum von fünf(5) Zeitpunkten als mental einfach zu empfinden. Einfachstes Beispiel ist der "Doppelschlag", eine von Barock bis Romantik häufige Verzierungsfigur, die in beiden ihren Notationsvarianten (in "zeit-loser" Vorschlagsnotation, oder "aus-notiert" als Vierer- oder Fünfer-Gruppe), Varianten kennt, die einer gleichmäßigen und "mental einfachen" Empfindung von funf Anschlägen entsprechen:
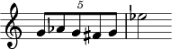
Anderes Beispiel: Die Blechbläser-Fanfaren im Satz Danse Sacrale von Stravinskys Sacre:
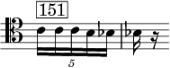
Diese Stelle im zweiten Teil ist explizit auf Kontrast gesetzt zu dem sehr ähnlichen Motiv der Solo-Trompete aus dem ersten Teil, Zf. 26, wo sehr ähnliche fünf Noten der abwärstleitenden Chromatik deutlich unterschieden als 3+2 und 2+3 ausgeführt werden.
Gegenbeispiel ist Bruckners Vierte, Finale, wo bei der Umarbeitung der Erstfassung im Seitensatz eine doch sehr blasse Quintole ersetzt wurde durch scharf gezeichnete und wohlunterschiedene Folgen 2+3, resp. 3+2.
Auch auf der Ebene der Taktgliederung gibt es viele überzeugende, teils gar berühmte Beispiele, so der Tanzsatz aus Cajkovskijs Sinfonie Pathétique, zweiter Satz:

Eine Folge von fünf kann also sowohl als einfach, wie auch als zusammengesetzt empfunden werden, je nach Inhalt und Kontext.
Die "mentale Einfachheit" endet spätestens jedoch beim Faktor sechs(6); hier wird sich immer, zumindest nach einiger Wiederholung, entweder die zwei-mal-drei oder drei-mal-zwei Gliederung im Empfinden einstellen. Dass die Unterscheidung dazwischen sehr praktisch-musikantisch und nicht nur notationstechnisch-theoretisch ist, zeigt sich unmittelbar, wenn man versucht folgenden Rhythmus (einmal oder immer wiederholend) zu realisieren:

Wenn das Ryhthmusempfinden einmal eingerastet ist, stellt das Ganze
selbstverständlich kein Problem dar. Dem Verfasser ging es allerdings so,
dass, als er mit den frohgemuten Worten "Ach, das sind ja nur immer die gleichen
Achtel" es ganz prima vista
anging, er beim zweiten Achtel des zweiten Taktes sich
merklich verhaspelte!
Es sind eben nicht immer dieselben Achtel!
Für die Gestalt des metrischen Rasters innerhalb eines Taktes bedeutet dieser Wahrnehmungs-Mechanismus, dass immer dann, wenn die Abfolge der Zählzeiten nicht als Ganzes als mental einfach empfunden wird, eine Unterteilung in mental einfache Gruppen stattfinden muss, bei mehr als fünfen(5), --- oder zumindest stattfinden kann, bei mehr als dreien(3).
Wir werden nun eine einfache Termsprache entwickeln, die diese Gruppenbildung repräsentiert. Diese dient in vorliegendem Text zur Diskussion des Problems, und soll zur Grundlage unserer eigenen Lösungen werden, sowohl in theoretischer Darstellung als auch in konkreter Implementierung.
Die angesprochene, aus psychischen Mechanismen geforderte Unterteilung "zu großer" Anschlagsgruppen kann umgekehrt auch gesehen werden als hierarchisch geschachtelte, schrittweise erfolgende Zusammenfassung von Grundereignissen. Das ist der Ansatz dem wir hier folgen werden.
Wir gehen aus von erwähnten Grundschlägen, für die eine oder auch mehrere Dauern ausgewählt werden. In den meisten Fällen wird es nur eine(1) Dauer sein. In den meisten Fällen wird dies eine der binär geteilten Grunddauern der CWN sein, also 1/1, 1/2, 1/4, 1/8, etc. Aber nicht immer, siehe die o.e. "mentale" Zählzeit der punktierten Achtel und Viertel, Abschnitt 2.6. Sogar n-olen-Werte können Grundschläge werden, siehe Abschnitt 3.1.4.
Unterhalb dieser ("notationellen", nicht unbedingt "mentalen") Grundschläge beginnt jeweils die Sub-Hierarchie der konventionellerweise implizit immer möglichen Zwei-Teilung. Diese ist aus CWN ubernommen. Soll hingegen auf einer tieferen Ebene eine andere Teilung als durch zwei(2) herrschen, so ist diese explizit anzugeben, und der notationelle Grundschlag muss halt entsprechend eine oder mehrere Ebenen unter den mentalen gelegt werden, s.o. Abschnitt 2.6.
Die Dauer des Grundschlages wird als rationale Zahl notiert.
4
Ist der Zähler gleich eins(1), so kann dieser weggelassen werden.
Ist die konkrete Dauer der Zählzeit in allen Teilen des Graphen
identisch konstant und im momentanen Diskussionskontext irrelevant, oder sogar noch
unbestimmt, ergibt sich z.B. erst
später durch Division der Gesamtdauer des Taktes, so kann diese Angabe auch ganz
weggelassen werden.
Es werden auf einer ersten Ebene
Anschläge dieser Grunddauer zusammengefasst zu mental einfachen Einheiten.
Seien diese Einheiten z.B. drei Gruppen der Längen a, b und c, dann
bezeichnen wir die Gesamtgestalt mit der Formel
a*1/n + b*1/n + c*1/n
oder auch
a*/n + b*/n + c*/n
oder auch
a + b + c
Falls alle Gruppengrößen übereinstimmen, nämlich d Gruppen der Länge e*1/n,
wird dies abgekürzt zu der multiplikativen Schreibweise
d * e * 1/n
oder vereinfacht
d * e * /n oder vereinfacht
d * e
2 2 3 3 3 3 3 3
/ \ / \ / \ / \ / \ / \ / \ / \
x x x x x x x x x x x x x x x x x x x x x x
2*/8+2*/8+3*/8+3*/8 3*/8+3*/8+3*/8+3*/8 = 4*3*1/8
2 + 2 + 3 + 3 3 + 3 + 3 + 3 = 4 * 3
|
Wenden wir auf der so entstandenen Folge von Gruppen ein noch strengeres Kriterium an und nennen "einfache Folgen" nur solche Folge mit nicht mehr als drei(3) Komponenten. 5 Es muss nun durch weitere Zusammenfassung jede nicht-einfache Folge von Anschlagsgruppen überführt werden in eine Folge von einfachen Folgen von Anschlagsgruppen:
2 2 2 2
/ \ / \ / \ / \
2 2 3 3 3 3 3 3
/ \ / \ / \ / \ / \ / \ / \ / \
x x x x x x x x x x x x x x x x x x x x x x
(2+2)+(3+3) = (2*2)+(2*3) (3+3)+(3+3) = (2*3)+(2*3) = 2*2*3
|
Ausgehend von der ursprünglichen, rein additiven Formel
repräsentieren wir diese zweite Hierarchie-Ebene durch runde Klammern:
(a+b+c)+(f+g+h)
Zunächst kann dann innerhalb der Klammenr
wird die vereinfachte multiplikative Schreibweise angebracht werden:
(d*e)+(f+g+h)
Sollten alle Klammerinhalte gleich sein, wird auch auf der
obersten Ebene die additive durch die multiplikative Schreibweise ersetzt:
(d*e)+(d*e) = 2*(d*e) = 2*d*e
Man beachte, das alle Operatoren unserer Termsprache weder kommutativ noch assoziativ sind, und das Klammern explizite Bedeutung tragen, also Operatoren sind. (Dementsprechend gibt es kein "Herausrechnen" des gemeinsamen Faktors bei (2*2)+(2*3), weil die abkürzende Schreibweise nur von unten aufsteigend definiert ist!)
Man lasse sich durch die Operatoren und ihre Anzahl nicht täuschen: die Schreibweisen 2+3+2 und 3*2 stehen beide für zwei Ebenen der Zusammenfassungs-Hierarchie; die Formeln 2*(2+3) und 2*2*3 für deren drei.
Theoretisch muss der Vorgang der Zusammenfassung "bis zur Erschöpfung" fortgesetzt werden, bis also ganz oben eine "mental einfache" Folge steht. Es müssen also die entstehenden Folgen von einfachen Folgen evtl. überführt werden in Folgen von einfachen Folgen von einfachen Folgen. Es ergibt sich allerdings in der Praxis kaum eine Gliederung mit mehr als den in den bisherigen Beispielen notwendigen zwei(2) Schichten von Gruppierungen.
Als Extrembeispiel könnte gelten
2 2
/ \ / \
/ \ / \
2 2 2 2
/ \ / \ / \ / \
3 3 3 3 3 3 3 3
/ \ / \ / \ / \ / \ / \ / \ / \
x x x x x x x x x x x x x x x x x x x x x x x x
((3+3)+(3+3))+((3+3)+(3+3)) = ((2*3)+(2*3)) + ((2*3)+(2*3)) = (2*2*3) + (2*2*3)
= 2*2*2*3
|
Dies wäre zu notieren als "24/16-Takt", und kann auch durchaus praktische Relevanz haben, wie weiter unten beschrieben. Diese drei Ebenen der Gruppierung sind aber allemal das Äußerste bezgl. der praktischen Anwendbarkeit, denn hinter der hier so abstrakt wirkenden mathematischen Gestalt steckt doch allemal die praktische Ausführung durch den ausübenden Musiker, die der fortschreitenden Komplexierung Grenzen setzt.
Im klassisch-romantischen Zweig der CWN sind zweifellos die homogenen, multiplikativ schreibbaren Metriken der Normalfall. Diese multiplikative Schreibweise darf aber nicht davon ablenken, dass der mentale Vorgang der Gruppenbildung (jedenfalls oberhalb der "mentalen Zählzeit") auch da ein additiver ist, nicht ein divisiver.
In anderen Stilen sind heterogene, also nicht multiplikativ schreibbare Taktarten hingegen zumindest gleichberechtigt, z.B. in Volksmusiken unterschiedlichster Provenienz.
Die aufgestellten Regeln für unsere Termsprache erlauben aber Baumstrukturen, die nicht so "ausgewogen" sind wie die Beispiele im vorigen Abschnitt.
Im folgenden versuchen wir die wichtigsten Kategorien von zunehmender Komplizierung herauszuarbeiten.
Ungleich vorhandene Ebenen:
Sobald man den Faktor "eins(1)" zuläßt, sprich: Gruppierungen, die nur eine
Komponente beinhalten, (und unsere Formulierung oben verbietet das mitnichten!)
können die Strukturen unbalanciert werden.
Dann kann z.B der berühmte und häufige "8/8-Takt" auf gleich drei Arten in unserer Termsprache modelliert werden, z.B.
2 2
/ \ / \
3 3 2 3 3 | |
/ \ / \ / \ / \ / \ | |
x x x x x x x x x x x x x x x x
3+3+2 (2*3)+2
|
Man beachte dass die Bedeutung und auch die Berechtigung beider
Terme durchaus vom Interpretationskontext abhängt:
Wenn konkrete physiologisch/mentale Zählprozesse modelliert werden sollen
ist wohl nur die linke Variante eine zutreffende Wiedergabe.
Die rechte Variante zielt auf eine abstrakte Strukturaussage, nämlich soviel
gleichlautende Sub-Terme wie möglich durch multiplikative Schreibweise zu
verdeutlichen. Eine zutreffende
Modellierung konkreter Zählvorgänge wird hier wohl nicht vorliegen.
Folgendes Beispiel hingegen zeigt einen un-balancierten Baum, der anders schwerlich schreibbar wäre, wo also die unterschiedliche Differenzierungstiefe beider Hälften tatsächlich dem musikalischen Empfinden entspricht:
1 3
/ / | \
3 2 2 2
/ \ / \ / \ / \
x x x x x x x x x
(1*3) + (3*2)
|
oder auch
3 3
/ \ / | \
/ | \ 2 2 2
| | | / \ / \ / \
x x x x x x x x x
(3*1) + (3*2)
|
Das dies mitnichten theoretische Ausgeburt ist, sondern durchaus nachvollziebare praktische Metrik, zeige ein Beispiel wie

Taktarten mit mehreren Grunddauern:
Dieses Bespiel bildet auch gleich den Übergang zur nächsten Kategorie. Wir
haben oben in unsere Termsprache die Angabe des Zählers /z eingeführt,
aber bisher nicht benutzen müssen.
In der Tat gibt es durchaus metrische Strukturen, in denen mehrere verschiedene
Grunddauern auftreten.
Vorangehendes Beispiel könnte man in unserer Termsprache ja auch beschreiben als
3/8 + 3/4
NB stellt das, wenn man es als Modellierung der mentalen/physiologischen Vorgänge auffasst, eine etwas andere Art des Zählens dar, als der oben gewählte Term, nämlich ein Wechsel von einzeln, als Grundschlag empfundenen Achteln zu Vierteln, die dann unterteilt werden, statt bei Achteln zu bleiben und diese nur anders zusammenzufassen.
Den Term als Modellierung des psychischen Apparates aufzufassen ist aber mitnichten erforderlich. Als reine Strukturaussage sind sich hingegen die Terme 3/8 + 3*(2/8) und 3/8 + 3/4 sehr ähnlich, da die Unterteilung der Viertel in zwei Achtel eh die "kanonische und ubiquitäre" ist und ohne weitere Deklaration immer latent stattfindet.
Ein weiteres Beispiel sei das Scherzo aus des Verfassers jüngst vollendeten Vierten Sinfonie:

Die Formel für diese Metrik könnte sein
3/4 + 5/8
also ein deutlicher Wechsel der Zählzeit.
Subtraktive Bildung:
Aber diese Formel ist für die praktische Interpretation keinesfalls zutreffend!
Gemeint ist vielmehr (und auch
deutlich ausgedrückt durch Motivik, Harmonik und Kontrapunkt)
eine Verkürzung, also ein "normaler" 6/4 oder 2*(3/4)-Takt, der um sein
allerletztes Achtel beschnitten wird, wo der Folgetakt also "zu früh hineinstolpert".
Dies auszudrücken wäre ein Term adäquat wie
(3/4) + (3/4 - 1/8)
oder
(3/4) + (/4 + /4 + (/4-/8))
Andere Grundwerte, z.B. Triolen:
Damit nicht genug, es gibt durchaus Erweiterungsversuche, auch andere
als die binär geteilten Grunddauern der CWN als Zählzeiten zu verwenden.
(In der Tat kombiniert das weit oben schon angeführte Beispiel des 12/16-Taktes
ja eine "nominelle" Zählzeit von einem Sechzehntel mit einer
"mentalen", die ein punktiertes Achtel dauert!)
Ungewöhnlichere Kombinationen können besonders bestimmt vom
Kontext durchaus sinnvoll sein.
Wenn z.B. in einem Vier-Viertel-Takt eine triolischer Füllung des gesamten
Taktes auftritt, also sechs Triolenviertel,
gefolgt von einem verkürzten Takt, der nur fünf(5) der Triolenviertel
enthalten soll. Dann kann ein "Fünf-Triolenviertel-Takt" genau das richtige
Mittel der Notation sein, besonders wenn es bald danach mit wieder vollständigen
Takten (sechs Triolenviertel, resp. vier Vierteln) weitergeht.
Oder auch innerhalb desselben Taktes:

Zeile eins zeigt die originale Weise wie Leonard Bernsteins
America notiert ist. Reichlich bieder, aber damals galt das
als progressiv. Unsere Formel dafür wäre
(2*3)+(3*2)/8
Zeile zwei ist eine viel aufregendere Variante, ein Rhythmus,
den heutzutage, dank der Erfahrung mit elektronisch produzierter Musik,
jeder bessere Rapper mit Lippen und Gaumen exakt hervorbringen kann,
und den der Verfasser auch immer meint zu empfinden, wenn er
an jenes Opus denkt. Hier tauchen gemischt Triolen-Achtel und Achtel
im selben Takt als Grundwerte auf.
Eine mögliche Formel ist
(2*3/12)+(3/8)
Dass dieser gar nicht sooo weit hergeholt ist zeigt Zeile drei, die ihn
auf ein den größten gemeinsamen Teiler umrechnet.
Eine mögliche Formel ist
(2*3*2)+(3*3)/16.
aber "mentale Zählzeit" sind natürlich nicht die Sechzehntel!
Dieses Beispiel kann aber auch zeigen, dass die Grenze zwischen "Metrik", als einem trotz wechselnden Inhalten gleichbleibenden Raster, welches die Wahrnehmung bewertet und einfärbt, und "Rhythmus", welches diesen Inhalt direkt ausdrückt, sich gegen das Wahrnehmungsraster verhält, aber dieses auch induziert und anstößt, in der praktischen Anwendung weniger deutlich sein kann als die theoretische Begrifskonstruktion es gerne hätte.
Verfasser hat leider keinen Zugriff auf originale Notate von Apocalypse in 9/4 von Genesis, aber er meint prinzipiell folgendes zu hören:

Der im Titel behauptete Neun-Viertel-Takt kommt nur zu Stande durch die
sich verschiebende Überlagerung der Bass-Achtel und der gleichmäßigen
Viertel der Rhythmusgruppe. (Die Oberstimme spielt eine freie Orgel-Melodie und
trägt nicht zur Definition der Metrik bei.)
Hier wäre also zwangsläufig notwendig ein weiterer Operator unserer
Termsprache, nämlich für parallele Komposition.
Ohne diesen kann der Takt zwar als 2*(4+3+2)/8 begriffen werden,
und als 18/8 benannt, es käme aber nie etwas zustande, was man "9/4"
nennen dürfte.
Durch die Überlagerung aber geschieht genau das! Nur die
gesamte Folge von neun Vierteln kann als wiederkehrend empfunden werden, und
nur "9/4" ist die korrekte Benennung, ohne dass
die Viertel selber in irgendeinder Weise
gruppiert werden! Nein, sie schweben halt gegen den Bass und werden nur
dadurch, gleichsam indirekt, umgefärbt.
Diese auf der Ebene der Metrik recht theoretisch klingende Analyse macht
aber im tatsächlichen Vollzug den sensationellen Reiz dieses Satzes aus.
Keine der zuletzt beschriebenen weiterführenden Varianten
erlaubt unsere bis hierhin definierte Termsprache.
Wir wollen sie auch zu diesem Zeitpunkt nicht erweitern! Denn wir vermuten,
dass jede Erweiterung nicht die letzte sein kann, d.h. dass in der
musikalisch/musikantisch/kompositorischen Praxis immer wieder neue metrische
Strukturen entwickelt werden, die von einem geschlossenen System, es sei weit
wie es will, nicht erfasst werden können.
Und das ist gut so!
Die bis hier entwickelte Termsprache ist eine Eigenschaft des
Mittelgrundes. Sie muss, um in konkrete Notation einzufliessen,
in eine Vordergrundgestalt übersetzt werden, also eine
Zeichenfolge, die tatsächlich in den Noten steht und dem Leser
die gemeinte Metrik mitteilt. Diese heißt Taktbezeichnung oder
auch Taktart-Angabe.
Diese Übersetzung ist jedoch "weder rechts- noch linkseindeutig",
und es gibt dafür sehr unterschiedliche Verfahren, je nach Stil, Genre und Epoche.
Die einfachste Methode, die
fast immer geht ist, ist die Schreibweise ähnlich wie ein einfacher "mathematischer
Bruch". Den Nenner bildet der Nenner der kleinsten als Schlag verwendete
Dauer, und der Zähler ist die Länge des Taktes gemessen in dieser Dauer.
(Das geht immer dann, wenn die verwendeten Zählzeiten auf die binär geteilten Gundwerte
der CWN beschränkt bleiben, weil dann deren kürzeste glatter Teiler aller anderen
ist.)
Dies ist die "klassische" Schreibweise von Taktarten, und nun sollte selbstverständlich sein, was ganz zu Beginn erwähnt wurde, dass diese Terme eben keine Brüche sind, und nicht "gekürzt" werden können.
Allerdings läßt sich an einer solchen Bezeichnung u.U. relativ wenig über die interne Struktur der Metrik ablesen, die Methode ist nicht "injektiv". So erzeugen die sehr unterschiedlichen Metriken (3*1/8) + (3*1/4) aus dem "heterogenen" Beispiel oben, und das total homogene 3*3/8 beide die Bezeichnung 9/8.
Im Rahmen von Notationsreformen und -erweiterungen beginnend im Neunzehnten und Zwanzigsten Jahrhundert haben sich auch Taktbezeichnungen entwickelt, die der Termstruktur der Mittelgrund-Darstellung (wie durch unsere kleine Termsprache) mehr oder weniger eng folgen. Damit sind Schreibweisen möglich geworden wie
2 + 3 3 5 2*3 1
----- --- + --- ----- - ---
4 4 8 4 8
|
In einer weiteren Erweiterung dieser Notation kann die Zahl im Nenner dieses "Bruch-ähnlichen" ersetzt werden durch das Notensymbol. Dies ist aber zunächst nur ein Auswechseln der Typographie, die "4" unter dem Strich meint auch schon die Dauer VIERTEL
Eine wirkliche Erweiterung ist, wenn dieses Symbol dann kein Grundsymbol mehr ist, sondern punktiert werden kann, oder unter einer Triolenklammer stehen, etc., also die Zählzeit keine der binären Grunddauern mehr ist.
Es gibt diese Erweiterung auch unter Beibehaltung der numerischen Schreibweise, wie
4 4
----- -----
6 16/3
|
Die erste Taktangabe bedeutet vier Triolen-Viertel pro Takt, die zweite vier punktierte Achtel.
In der Literatur findet man verschiedene Versuche von Übersichten und Zusammenfassungen dieser Erweiterungen. Man sehe besonders die Notationkompendien von Gould und Read, (teilweise auch Stone), wie ausführlich aufgelistet in dem Artikel senza tempo 2012070100 --- Synopsis of Musical Notation Encyclopedias.
Aber alle diese, so löblich und nützlich und wichig sie sind, können unser Bedürfnis nach Systematik in der Behandlung nicht befriedigen, da sie die Vordergrundphänomene besprechen, die Darstellungsebene, ohne die Frage nach einer Semantik, nach einem mathematischen Kalkül als Mittelgrund, auch nur aufzuwerfen.
Bei der musikalischen Interpretation im Rahmen der
konventionellen westlichen Praxis liegt aber der genau inverse
Anwendungsfall vor: Wir sehen eine Taktart-Angabe, und müssen die
nun folgenden Notenfolgen im Sinne der dadurch gemeinten Metrik
interpretieren.
Mehr formal: Wir müssen zumeist aus einer stark
vereinfachenden Bezeichung "z/n", gebildet nach
dem in Abschnitt 2.10
beschriebenen simpelsten Benennungsverfahren,
den Term unserer Metrik-Sprache ableiten, der die gemeinte Taktstruktur
repräsentiert.
Dies genau ist der Übergang von Vordergrundstruktur in (eine mögliche) Mittelgrundstruktur, der in der Fachliteratur so gerne unterschlagen wird.
Bei der konventionellen Angabe "z/n" ist "n" die Bezeichnung einer Grunddauer "1/n", (also 1/1, 1/2, 1/4, 1/8, allgemein 2^(-k)), die als Zählzeit dient. Diese ist, wie oben ausgeführt, relativ beliebig. Man braucht also nur den Zähler "z" zu betrachten.
Dabei gelten u.a. folgende Sätze:
Die erste und eine der letzten Fragestellungen
können auch kombiniert auftreten: nicht-prime Zahl mit einem
Primfaktor größer/gleich fünf, wie "15/8" oder "14/16".
Betrachten wir Frage der Hierarchiedefinition innerhalb des Taktes
zunächst für die einfachsten der historisch etablierten Taktarten.
Diese haben die Gestalt
"2^a*3^b / n",
(mit n=2^(-k), also vernachlässigbar, s.o.),
a=0 und b>0:
Dies ergibt eine Hierarchie von Dreiteilungen, also "perfekte" Teilungen
in der Sprache der älteren Epoche. "9/16" Takte sind durchaus häufig,
"27/x" aber wohl seltene Ausnahmen.
So steht der allerletzte Satz der Beethovenschen Klaviersonaten, das Variationenfinale von Opus-hundertelf, ein Gipfelwerk westlicher Musik schlechthin, der schöne Wiesengrund, fast durchgängig im 27/32 6 ! Und in C-Dur! Apotheose der perfekten Teilung!
a=1 und b=0 und
a=2 und b=0:
Dies sind die "geradesten" Takte wie "2/2" und "4/4".
Inwieweit "4/4" primitiv ist, also
das psychische Empfinden tatsächlich vier(4) Positionen linear hintereinanderstellt,
oder ob eine Hierarchie "zwei mal zwei" empfunden wird, ist wohl von
Inhalt und Stil abhängig; prinzipiell erscheint beides möglich.
a>=3 und b=0:
Dies aber sind gerade
keine geraden Takte mehr! Vielmehr kann eine solche Taktart,
(im Rahmen der konventionellen Methode der Taktartbezeichung), immer nur
additiv gemeint sein, also 8/8 als z.B. (3+3+2)/8. Warum?
Wären bei dem Acht-Achtel-Takt tatsächlich acht gleichmäßig folgende
Ereignisse gemeint, so würde das Empfinden von Hörer und Musiker diese lange Folge
eben nicht gleich-berechtigt, sondern in irgend einer Zweier-Gruppierung
empfinden. Die Taktangabe könnte, ja, müsste entsprechend
"gekürzt" werden, auf entweder "4/4" oder
"2/2". Dass aber "8/8" geschrieben steht kann nur begründet werden
dadurch, dass eben diese "kürzbare" Hierarchie nicht gemeint ist.
Entsprechend stünde z.B. 16/16 für 2*(3+3+2)/16 oder auch (2*3 + 2*2 + 2*3)/16.
a=3 und b=1:
Bei "24/16" gibt es diese Kürzbarkeit dann und nur dann nicht,
wenn die Drei-Teilung ganz unten in der Hierarchie liegt. Dann
ist "24/16" eine
durchaus übliche Bezeichnung für einen "ganz normalen" 4/4 Takt, bei dem
jedes Achtel in drei Sechzehntel-Triolen aufgelöst wird, die man aber ohne
die lästigen Triolenklammern einfach als Sechzehntel hinschreiben möchte.
In unserer Termsprache also (2*2*2*3)/16.
Als Konsequenz muss man dann natürlich alle längeren Grundwerte
punktieren, so dass die mentale Zählzeit hier das punktierte
Viertel oder gar das punktierte Achtel ist, -- dies ist ein in der Praxis
doch oft vorkommendes Beispiel für o.e. Verschiebung der Zählzeit-Grenze.
a>0 und b>0:
Ähnliche Überlegungen führen hier dazu, dass bei allen konventionellen
Taktangaben der CWN, in denen der Zähler die Faktoren zwei und drei mischt, die
Zweierpotenz als ganze vollständig oberhalb der Teilungen durch drei(3) liegt.
Dies deshalb, weil die Möglichkeit der Teilung durch zwei(2) ja den Notendauern
(unterhalb und einschliesslich der Zählzeit) inhärent ist und immer, ohne weitere
Maßnahmen, eh ubiquitar zur Verfügung stünde, also nicht durch eine Metrik-Angabe
gefordert werden muss.
Eine Teilung durch zwei(2) am unteren Ende der
Hierarchie könnte also auf einfachste Weise durch ein Verschieben der Wahl der
Zählzeit auf die nächst höhere Ebene ausgedrückt und mit dem
fundamentalen Mittel der Dauern-Halbierung realisiert werden, im Organisationsbereich
unterhalb der Zählzeit-Grenze.
Das gilt hingegen nicht für die zwei(2), die oberhalb einer durch
die Taktart begründeten Dreier-Gliederung angesiedelt
ist, die also nur multiplikativ realisiert werden kann,
und deshalb in die Taktangabe einfließen muss.
Deshalb werden die Zweier-Faktoren der Taktart-Angabe als derartig oben-liegend
aufgefasst, denn die unten-liegenden bedürfen ja der Taktart nicht!
Es ergeben sich damit z.B. folgende metrische Hierarchien:
9/8 3/4 6/8 12/8
(und nicht etwa 2
3 3 2 3 2
3 3 2 3
xxx xxx xxx x x x xxx xxx xx xx xx) xxx xxx xxx xxx
|
Die metrische Struktur (3*2*3)/16, die also aus drei Sechs-Sechzehntel-Gruppen besteht, kann durchaus sinnvoll sein. Z.B. ein 3/4 Takt, in dem auf jedem Achtel eine Sechzehntel-Triole steht, ist keinesfalls etwas aussergewöhnliches, siehe nur Beethvoen, den langsamen Satz der Klaviersonate op.3 Nr.1, Takt 37 bis 44. Die dort gemeinte Teilung 3-2-3 ist rein im Organisationsbereich der Taktart im CWN-System nicht benennbar. Sie kann nur realisiert werden wenn eine der Grenzen zwischen den Organisationsbereichen mitten durch sie hindurch geht, z.B. durch einen 3/4-Takt mit expliziten Sextolen, wie in genanntem Beispiel, oder durch Dreier-Gruppen von 6/8-Takten.
Das ist eines der ganz zu Beginn dieses Artikels (Abschnitt 1.3, unter "drittens") angekündigten Beispiele, wo eine rein systematisch durchaus einfache mögliche Konstruktion des Mittelgrundes keine Entsprechung in der Vordergrund-Notation hat: Im CWN ist halt aus historischen Gründen eine Zwei-Teilung zwischen zwei Drei-Teilungen nicht vorgesehen.
Die entstehenden "achtzehn Sechzehntel" würden durch eine einfache Angabe wie "18/16" gemäß obiger Regel nämlich als 2-3-3 (von oben nach unten) interpretiert, nicht als 3-2-3, was wir bräuchten:
18/16 wird konventionellerweise aufgefasst als
3 2
2 3
3 3
xxx xxx xxx xxx xxx xxx xxx xxx xxx xxx xxx xxx
|
Dies unterscheidet die auf pragmatisch-tänzerischer Tradition beruhende
metrische Notation von der eher theoretisch-theologisch fundierten
der Mensuralnotation, in der eine vollständig freie Kompositionalität
aller Teilungen galt, s.o.
Auf diese charakteristischen Fehlstelle weist auch Gieseking schon hin
[gieseking, Seite 103].
Mit dieser Zusatzregel ergibt sich für alle Taktart-Angaben der Form "2^a*3^b / z" folglich im Rahmen der Konventionen eine eindeutige Metrik als entsprechende Mittelgrundstruktur.
Treten Primfaktoren größer als drei zusammen mit dem Faktor zwei auf, so kann in Analogie zum vorigen Kapitel festgelegt werden, dass die Zweierpotenzen immer die aller-obersten Teilungsebene bilden sollen. Während dies in den vorhergehenden Fällen (in Verbindung mit dem Faktor drei) durch allerorten verbreitete Konvention begründet ist, wäre diese analoge Anwendung zwar eine "natürliche Erweiterung", aber auch recht beliebig, denn die CWN-Tradition kennt sehr wenige "10/4" Takte und ähnliches.
Ein solcher läßt sich allerdings bequem ohne weitere Maßnahmen konstruieren,
da wir oben bereits festgestellt haben, dass auch eine Fünfer-Teilung
vom Musiker als "einfach" empfunden und realisiert werden kann.
Folglich könnten die Schichtungen 2*5 als auch 5*2
unmittelbar eine Taktart konstruieren.
Die Fünf kann aber auch als "zusammengesetzt" empfunden werden,
und ein 10/8-Takt also auch als (3*2)+(2*2) verstanden,
oder als 2*(2+3), etc.
Anders schon bei größeren Primzahlen, und auch bei größeren nicht-primen. Hier ist mentale Einfachheit unmöglich, und auf mindestens einer Teilungsebene ist eine asymmetrische, additive Organisation wahrscheinlich, --- bei den Primzahlen zwangsläufigerweise, bei den teilbaren, wie acht(8) und neun(9) als Alternative zur "trivialen" multiplikativen Teilung.
So sind folgende Zerlegungen durchaus üblich:
5 = 2 + 3 5 = 3 + 2 5 = 2 + 2 + 1 7 = 2 + 2 + 3 7 = 2 + 3 + 2 7 = 3 + 2 + 2 8 = 3 + 3 + 2 8 = 3 + 2 + 3 8 = 2 + 3 + 3 9 = 4 + 5 9 = 4 + 3 + 2 9 = //etc. |
Im hierarchischen Aufbau des takt-internen Metrik entspricht eine solche Teilung natürlich zwei Ebenen der einfachen multiplikativen Gestaltung. Der Unterschied ist nur, dass auf der unteren der beiden Ebenen halt nicht dieselben, sondern verschiedene Faktoren stehen, der "Plus-Operator" also nicht durch das "Mal" ersetzt werden kann:
|
9 = 3 = 3 | 8 = 3 =
/ | \ * | / | \
3 3 3 3 | 2 3 3 2 + 3 + 3
|
|
Rein theoretisch kann eine solche asymmetrische Zusammenfassung (genau wie zwei multiplikative Ebenen) in einen größeren hierarchischen Aufbaus der internen Takt-Metrik eingebaut werden, siehe obigen 10/8 Takt als 2*(3+2)
Praktischerweise aber ist eine solche Kombinierbarkeit wohl selten gegeben, wenn man die konkrete Ausführung durch menschliche Musiker voraussetzt, die verbietet, dass die reine Anzahl der (mentalen) Zählzeiten pro Takt zu groß wird.
So ist selbstverständlich ein "15/16" vorstellbar als (2*3)+(3*3)/16
oder als (3*3)+(2*3)/16 oder als 5*3/16.
Dabei ist 1/16 die nominelle und 3/16 die mentale Zählzeit, und man zählt
"fünf punktierte Achtel", entweder als "zwei plus drei" oder als
"drei plus zwei", oder gar "einfach".
Dasselbe als "drei-über-fünf" ist auch noch denkbar, allerdings bietet sich
dann wohl an, die obere Grenze der Organisationsbereiche zu verschieben,
und schlicht Drei-Takt-Gruppen von simpleren 5/x-Takten zu notieren.
Theoretisch jedoch fügen sich diese additiven, asymmetrischen Schichten
kanonisch in einen Gesamtaufbau ein.
Im Falle der konventionellen Taktartbezeichnungen ist allerdings nur
eine der hierarchichen Schichten derart additiv, die darunter und
darüber sind wie im multiplikativen Fall homogen. Besonders für die Ebene
darunter, die "x", die durch die additive Formel zusammengefasst werden, gilt,
dass diese untereinander identisch sind, z.B. alles Achtel oder alles Viertel.
Unterhalb von "x" gilt das oben für die regelmäßigen Takte
Gesagte, dass nur eine Teilung größer zwei(2) in die Taktartbezeichnung
einfliesst, weil die Teilung durch zwei eh ubiquitär ist.
Aber auch am oberen Ende der Takthierarachie ist eine "reine zwei" oft
überflüssig und kann einfacher als innerhalb der Metrik
im oberen Organisationbereich realisiert werden,
als Wiederholung von Takten.
Dies alles sind aber Eigenschaften der traditionellen Metriken. Unsere theoretische Termsprache erlaubt hingegen ("frei kompositional") additive Zusammenfassung auf mehreren Ebenen, auch von unterschiedlichen "x".
Im Organisationsbereich oberhalb der Takte erwähnten wir bereits die Bildung von Taktgruppen (explizit durch textuelle Anweisungen oder implizit, durch die Interpretation das Inhaltes) als wichtiges Mittel der Getaltung.
Ebenfalls in diesem Bereich findet statt, als konkreteres und folgenreicheres Mittel, der Wechsel zwischen verschiedenen Metriken. In der zusammenfassenden Literatur (siehe die Übersicht in senza tempo 20120701 00 --- Synopsis of Musical Notation Encyclopedias) gehen allein schon die Benennungen von wechselnden Metren wüst durcheinander, geschweige denn die Begriffe.
Jedoch sind die Gegebenheiten bei taktweise, also höchst-frequent, wechselnden Metriken recht einfach nach folgenden unabhängigen Kriterien zu sortieren:
Je nachdem können sich unterschiedliche Konsequenzen für die Notation ergeben:
Ist die Abfolge regelmäßig, so stellt sich zunächst die Frage, ob die
obere Grenze der Organisationsbereiche nicht nach oben geschoben werden sollte,
also aus der Folge von Metriken eine einzige Metrik konstruiert werden.
So kann eine regelmäßige Abfolge von 3/4 und 4/4 Takt ja durchaus zu einem
7/4-Takt zusammengefasst werden, entsprechend der metrischen Formel
(3+4)/4
Die dadurch verschwindende Taktgrenze kann ja immernoch als punktierter
Taktstrich in der Notation ihre Spur hinterlassen.
Umgekehrtes gilt, wenn die (nominelle)
Taktdauer gleich bleibt. Hier gibt es Notationsformen,
die nur einmal die Menge der zur Auswahl stehenden Metren angibt, z.B.
mit Klammern geschrieben, wie in Nr. XX der Diabelli-Variationen
3/2(6/4)
oder mit Gleichheitszeichen
4/4 = 3+5/8 = 5+3/8
-- danach aber auf jedesmalige Notation des Wechsels der Metrik verzichtet.
Dies ist möglich, da die gleichbleibende Gesamtlänge jede Diskrepanz zwischen (rhythmisiertem) Taktinhalt und Metrik-Angabe niemals "ganz falsch" werden läßt. Besonders wenn in verschiedenen Stimmen eh verschiedene Metriken sich gegenüberstehen, kann ein solch impliziter Wechsel angemessen sein. Die wechselnden Metren können ja meist an der Bebalkung abgelesen werden, oder aber es werden auch hier punktierte Binnen-Taktstriche eingefügt.
Es können sich auch beide Aspekte kombinieren. Eine Notation wie
(3+4)/4 = (4+3)/4
könnte anzeigen, dass eine Folge von gleich-langen sieben-Viertel-Takten folgt,
deren jeder spontan wechselnd ohne weitere Anzeige in beiden Polaritäten stehen kann.
Dies sind aber notabene alles nur Aspekte des Vordergrundes! Im Mittelgrund wird schlicht je Takt (oder gar je Takt und Stimme) die jeweils gültige Metrik bestimmt, egal, wie häufig diese (von "aussen" gesehen) wechselt oder bleibt.
Komplementär zu den wechselnden Metriken spielt sich die Notation von Dauern und Rhythmen (fast) ausschliesslich in den beiden unteren Organisationsbereichen der Metrik ab, also innerhalb eines Taktes, hinabreichend bis (beliebig weit) unterhalb der Zählzeiten. Rhythmen werden in der taktbasierten Notation (bis auf ganz wenige exotische Ausnahmen, s.u.) ausschliesslich innerhalb eines Taktes notiert. Über die Taktgrenzen klingende Ereignisse, deren es sehr viele gibt, werden tatkweise zerlegt und durch "Haltebögen" (s.u. diesen Abschnitt) wieder zusammengefasst. Dies entspricht der gundlegenden Orientierungsfunktion des Taktes in der taktbasierten Notation (und darum heißt diese so !-)
Der Inhalt eines Taktes ist stets, wie erwähnt, eine beliebig gemischte, aber lückenlose Folge von Noten- und Pausen-Ereignissen, deren Summe der Länge des Taktes bei gegebener Taktart entspricht. Seien die Dauern der Ereignisse dieser Folge nun gegeben als von der Notation unabhängig und sollen nun metrisch korrekt für eine bestimmte Taktart notiert werden. Je nach Position eines Ereignisses im Takt muss dessen Dauer auf unterschiedliche Art in Notation übersetzt werden.
Dies ist deshalb problematisch, weil es zur Darstellung einer gegebenen musikalischen Dauer (z.B. kodiert als eine bestimmte rationale Zahl) sehr unterschiedliche Möglichkeiten gibt, unter denen auszuwählen ist. Diese ergeben sich durch die Kombination von
Sei eine darzustellende Dauer als rationale Zahl gegeben, wobei, wie oben erwähnt, "1" für die Ganze Note stehe, "1/4" für eine Viertel, und "1/3" für die Dauer, die dreimal in eine "1" passt (also die herkömmliche "Halbe-Triole"), etc.
Zunächst einmal kann für jede zu notierende Dauer ein Grundsymbol ausgewählt werden. Üblich sind in der metrischen Notation heutzutage noch: "Brevis" mit Wert 2, die "Ganze" mit 1, die "Halbe" mit 1/2, die "Viertel" mit 1/4, und so weiter.
Die Grundsymbole erlauben also Dauern von d1=2^n, wobei meist gilt n<0. Diese Dauern d1 nennen wir auch Grunddauern.
Die graphische Erscheinung der Grundsymbole ist nur teilweise systematisch und ergibt sich durch ihre Ableitung aus den entsprechenden Symbolen der Mensuralnotation, besonders aus der dort über Jahrhunderte sich erstreckenden Tendenz zu immer kürzeren Notenwerten als Bezugsgrößen.
Ihre Systematik 7 ist ...
| Name | Symbol | Wert | Kopf-Form | Kopf-Farbe | Hals | Fahne(/Balken) | Pausensymbol |
| Brevis | | 2 | eckig | hohl | -- | | |
| Ganze | | 1 | rund | hohl | -- | | |
| Halbe | | 1/2 | rund | hohl | ja | 0 | |
| Viertel | | 1/4 | rund | schwarz | ja | 0 | |
| Achtel | | 1/8 | rund | schwarz | ja | 1 | |
| Sechzehntel | | 1/16 | rund | schwarz | ja | 2 | |
| Zweiunddreissigstel | | 1/32 | rund | schwarz | ja | 3 | |
| etc. | 2^(-n-2) | rund | schwarz | ja | n |
Folgen mehrere Noten mit "Fähnchen" aufeinander, so können statt der einzelnen Fähnchen auch durchgehende Balken geschrieben werden. Obwohl sie zunächst nur als eine Vereinfachung des Schreibvorganges entstanden ist, ist diese Notationsform für unser Thema höchlichst relevant: Die zusammenfassende Wirkung der Balkengruppen, wie auch eventuelle Unterteilungen durch Unterbrechung aller oder einiger Balken, müssen nämlich ebenfalls die hierarchische Gliederung der Taktmetrik widerspiegeln. Damit ist das Finden der korrekten Balkensetzung wichtiger Teil unseres Generalthemas.
Durch das Setzen einer n-olen Klammer kann jeder dieser Werte statt in zwei(2) in n Werte der nächst-kleineren Stufe geteilt werden. So kann eine "Halbe Note" in drei(3) "Triolen-Viertel" aufgeteilt werden. 8 Die Dauer eines jeden Triolen-Viertels beträgt (logischerweise) 1/6. Ebenso kann eine ("normale") Viertel in drei Triolen-Achtel unterteilt werden, deren Dauer je 1/12 beträgt.
Ein Triolen-Viertel selbst wird behandelt wie ein "normales" Viertel: Es kann z.B., ohne dass eine weitere notationelle Maßnahme notwendig wird, in zwei Achtel oder vier Sechzehntel zerlegt werden. Deren Dauer ist logischerweise entsprechend kürzer als die der aus "normalen" Vierteln entstandenen, also 1/12 resp. 1/24.
Das Achtel, das durch Halbierung eines Triolen-Viertels entsteht ist also (rein mathematisch, rein nominell) gleichlang wie das Triolen-Achtel, dass durch Dreiteilung eines "normalen" Viertels entsteht. Dennoch sind sie notationell zunächst verschieden. Auch wird ersteres in der Musizier-Praxis nicht in allen Kontexten als "Triolen-Achtel" benannt werden, sondern u.U. ähnlich wie "das zweite Achtel in dem Triolen-Viertel" oder "das vierte Achtel in der Viertel-Triole". Auch können die intra-psychischen Prozesse im Musiker bei ihrer Hervorbringung und die beim Rezipienten ausgelösten Empfindungen in beiden Fällen durchaus unterschiedlich sein. Dies alles ist, wie erwähnt, stark von Kontext, Stil, Gattung und Epoche abhängig. Die Hierarchie der metrischen Teilung ist eben in beiden Fällen eine andere, es ist etwas fundamental anderes, erst durch zwei und dann durch drei zu teilen, oder umgekehrt.
Der rein mathematischer "Dauernwert" der Endresultate hingegen in beiden Fällen identisch, besagtes 1/12.
Meist gilt bei diesen n-olen n=3, Triolen sind die häufigsten n-olen. Aber grundsätzlich sei für n (zunächst) jede ungerade natürliche Zahl möglich. (Gerade Zahlen sind nicht erforderlich, wenn es nur um die Erzeugung von Dauernwerten geht. Sie sind nur in bestimmten metrischen Kontexten sinnvoll: bei sog. "Sextolen" und in Taktarten mit ungeraden Faktoren. Sie werden weiter unten behandelt, Abschnitt 3.1.3).
Somit erweitert sich die Menge der darstellbaren Dauern auf d2= d1 * t1^-1 * t2^-1 * ... *tn^-1, mit tk beliebige ungerade natürliche Zahl größer eins.
Man beachte aber, dass im Rahmen der konventionellen Rhythmusnotation eine Dauer mit einer Dauer d*tk^-1 nicht "eigenständig" notiert werden kann, sondern dass zu ihrer Herleitung eine Note der nächst höheren Teilungsebenen, also der Dauer d in tk Teile zerlegt werden muss. Die konstruierte Dauer wird also im selben Teilungsschritt mit tk-1 "Geschwistern" konstruiert, die im Notat zwangsläufig auftauchen müssen und in irgendeiner Form Verwendung finden müssen zur Notation von vorangehenden oder nachfolgenden Ereignissen. Eine "isolierte Triolenachtel" z.B. ist (in diesem Zusammenhang) ein Widerspruch in sich, wenn sie auch in Aussagen über Musik auftreten kann, oder in avancierteren, eher additiv bestimmten Verfahren der Metrik-Definition, siehe unten Abschnitt 3.1.4.
Zum dritten kann durch eine Punktierung (oder "Verlängerungspunkt" oder "Wertpunkt") die Dauer jeder (nach Schritt eins und zwei bestimmten) Einzelnote um ihre Hälfte verlängert werden, also auf das 1 1/2-fache ihres Grundwertes. Zwei Punkte verlängern auf das 1 3/4-fache, drei auf das 1 7/8 fache. Es kommt also mit jedem Punkt die Hälfte der vorigen Verlängerung dazu.
Diese Notation hat den Sinn, dass die Kombination zweier Noten die im rhythmischen Verhältnis 1:3 (oder 7:1 oder 1:15, etc) stehen, in sehr vielen Stilen, Gattungen und Epochen recht häufig sind, und sich deshalb eine sie unterstützende sparsame Spezialnotation entwickelt hat.
Die durch die Kombination aller drei Mittel darstellbaren Dauern sind also d3 = d2 * (2-2^(-p)), mit p>=0.
Zuletzt können durch Haltebögen (engl. "tie") mehrere Notensymbole zu einem Ereignis additiv zusammengefasst werden. Wichtig ist, dass der Haltebogen einzig auf der Ebene der Dauernberechnung definiert ist, und in der konkreten Ausführung alle nicht-ersten Noten keiner merkbaren Parameteränderung entsprechen. Das unterscheidet den Haltebogen fundamental vom "Bindebogen" (engl. "slur") und vom "Phrasierungsbogen".
Seine rein auf die Dauernberechnung bezogene Semantik wird dadurch verschleiert, dass einige Informationen in alle aneinander angebundenen Notensymbole redundanterweise einkodiert werden müssen: Soll eine Spielereignis mit der Tonhöhe "e-eins" für die Dauer 9/8 notiert werden, so kann dies nur durch Addition von Dauern ausgedrückt werden, z.B. indem eine Ganze und eine Achtel mit einem Haltebogen verbunden werden, oder eine punktierte Halbe und eine punktierte Viertel. In beiden Fällen müssen aber beide Notensymbole nun die Tonhöheninformation "e-eins" ausdrücken. Dies ist redundant, da ja nur ein einziges Spielereignis gemeint ist, aber die CWN erlaubt es halt nicht, Notensymbole überhaupt hinzuschreiben, die nur Längen aber keine Tonhöhen bezeichnen. 9
Die Tatsache, dass das zweite Notensymbol auch die Tonhöhe e-eins bezeichnet, ist aber streng genommen mitnichten eine Tonhöhen-Information! Vielmehr besagt diese Tatsache (in Verbindung damit dass die zweite Note keine weiteren Attribute wie Spielanweisungen etc. trägt) umgekehrt eben nur, dass das graphische Symbol des Bogens tatsächlich ein Halte-Bogen ist (und nicht etwa ein Bindebogen, etc.), dass also von dem graphischen Symbol der zweiten Note nur die Dauer relevant ist, und diese zur Dauer des vorangehenden Notensymboles dazuzurechnen ist, um die Gesamtdauer desjenigen Ereignisses zu bestimmen, dessen übrigen Parameter (Tonhöhe, Lautstärke, Artikulation, etc.) ausschliesslich durch das erste Notensymbol bestimmt werden. Dies ist ein komplizierter, aber typischer und häufiger Fall von Windschiefigkeit zwischen Vordergrundgestalt und Mittelgrundgehalt.
Diese Art der "Überbindung" kann beliebig oft angewandt werden, also auf mehr als nur zwei(2) Noten.
Damit sind alle rationalen Zahlen als Dauernwerte darstellbar.
Beweis:
Sei p/q die darzustellende Dauer, so ist 1/q durch Auswahl eines Grundwertes
(entsprechend der Potenz von 2 in der Primfaktorzerlegung von q)
und durch geschachtelte n-olen Klammern (entsprechend den anderen Faktoren darin)
darstellbar. Davon können nun p aufeinanderfolgende Exemplare
ganz schematisch durch Haltebögen addiert werden.
Dass die so erzeugte Notationsform in den meisten Fällen nicht praktikabel ist, leuchtet ein; dies genau ist ja unser Grundproblem der adäquaten Notierung.
Die Mehrheit der konventionellen Kompendien musikalischer Notation stellt n-olen nur als Variante zur Notation von Rhythmen dar. Gieseking weist zumindest darauf hin, dass sie unser Ausgangsproblem erheblich erschweren können, dass sein und Byrds Algorithmus damit nur partiell umgehen kann, und dass sie am besten durch Wechsel in ein "temporäres lokales 'Untermetrum'" zu behandeln wären.
Ausgehend von der oben aufgestellten Definition der drei Organisationbereiche läßt sich das Auftreten von n-olen und die Abschätzung der Konsequenzen auf die Metrik aber durchaus präziser verorten:
Am wenigsten kritisch sind die n-olen, die sich im unteren Organisationsbereich befinden, also unterhalb der Zählzeit. Dort sind sie scheinbar ein "rein rhythmisches" Phänomen. Bei genauerer Betrachtung wird auch dort eine "lokale Metrik" instantiiert, diese kann aber mit dem gewichtsbasierten Algorithmus (in der Ausbauform durch Gieseking) behandelt werden.
Dann aber können n-olen auch im mittleren Organisationsbereich auftreten und so die metrische Hierarchie in eine konsequenzenreich andersartige überführen. Dies ist im Falle von synkopiert einsetzenden n-olen von diesen Algorithmen nicht mehr adäquat auflösbar, siehe das Beispiel bei [gieseking, S. 112].
Zuletzt können sie sogar in bestimmten Notationsstilen Taktgrenzen überschreiten, somit zwei Takte zu einer neuen (lokalen) Metrik kombinieren und also gar im obersten Organisationsbereich angesiedelt sein.
Vordergrundrepräsentation und Semantik der n-olen haben sich historisch entwickelt, und führen zu bestimmten Widersprüchen, die wir hier zunächst deutlich herausarbeiten müssen, um dann eine Lösung vorzuschlagen. Ihr Grundprinzip ist zunächst einfach und scheint eindeutig, und dieses und die konfligierenden Konsequenzen sollen an einfachen Beispielen dargestellt werden.
Wie bereits ausgeführt sind die einfachsten n-olen die Triolen.
Im einfachsten Falle wird
eine gut als solche erkennbare Gruppe von drei gleichlangen Notenwerten
über ihrer mittleren Note mit einer kleinen Ziffer "3" bezeichnet.
Das soll bedeuten, dass in der Gesamt-Hierarchie der Notendauern auf genau
der Teilungsebene, die die Gesamtdauer der Gruppe in die Dauer der Einzelnoten
überführt, der übliche Faktor zwei durch den Faktor drei ersetzt wird.
Die Erkennbarkeit der Gruppe ergibt sich entweder schon durch ihre
Bebalkung, oder wird durch eine zusätzliche eckige Klammer (älterer Usus: runder Bogen)
hergestellt.
Der historische Entwicklungsprozess bringt nun die Forderung hervor,
dass diese Konstruktion in mehreren Dimensionen
völlig frei kompositional eingebettet werden könne.
Zum einen (a) sind statt der drei auch beliebig andere Faktoren erlaubt anzugeben,
und zum andern (b) können alle Methoden der Dauernkonstruktion- und Notation,
wie im vorigen Abschnitt beschrieben, also Unterteilung, n-olen, Punktierung
und Überbindung, auf die Einzelnoten der Gruppe angewandt werden,
genau wie auf beliebige "normale" Noten ausserhalb einer solchen.
Einziger Unterschied sind die sich ergebenden Dauernwerte,
bei denen halt eine "Verkürzung um den Faktor 2/3" stattgefunden hat.
Statt alle Einzelnoten der Gruppe zu erzeugen, wie oben formuliert, kann statt
mehrerer solcher auch ein(1) entsprechend längeres Notensymbol
verwendet werden, siehe nächstes Beispiel. Man kann sich das auch
erklären durch eine neu hinzutretende, bisher nicht nötige Operation,
(c) die Verschmelzung von einer echter Untermenge der erzeugten Einzelnoten.
Die Kombination dieser Verfahren jedoch führt relativ schnell zu Widersprüchen
in dem Sinne, dass die Vordergrundgestalt der Notation links- oder gar
recht-uneindeutig wird.
Dies ist aber lediglich eine technische Frage der Notation, und
neuere Verfahren haben dieses Problem behoben und tatsächlich volle Kompositionalität
erzielt.
Da der historische Vorgang bis zur endgültigen Klärung des Problems aber so
typisch ist, soll er hier in Kürze dargestellt werden.
Zunächst einmal erscheint kein Problem:
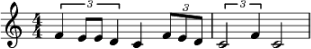
Die erste Gruppe nennt man "Viertel-Triole", die drei darin auftretenden
Dauernwerte "Triolen-Viertel" (oder ungenau auch "Viertel-Triole").
Drei "Viertelnoten-Symbole" nehmen die eigentlich für nur
zwei davon zur Verfügung stehende Dauer ein.
Es sind also "Sechstelnoten", ihre rechnerische Dauer beträgt 1/6.
Die mittlere Viertel wird durch das ubiquitäre Mittel der Zweiteilung in
Achtel aufgespalten, der Länge 1/12.
Die zweite Gruppe ist entsprechend eine "Achtel-Triole".
Die Achtel sind alle gleich lang, nämlich 1/12. Es ist für die berechnete
Dauer ja egal, auf welcher Ebene der Dauern-Hierarchie der Faktor zwei durch
die drei ersetzt wird. (Für das "feeling" des Interpreten, die Art des
Zählens und Messens, können u.U. aber beide Varianten etwas
fundamental anderes hevorrufen, wie oben erwähnt.)
Die dritte Triole zeigt eine Viertel-Triole, bei der die ersten beiden der durch die Triolierung enstandenene drei Viertel zu einer Halben zusammengefasst sind, gemäß obiger Operation (c) "Verschmelzung".
Unterhalb der Triolierung können, nach Forderung (b), alle Maßnahmen der Dauernableitung angewandt werden, was die Notation u.U. schwer zu lesen macht, und die Klammer um die Gesamtgruppe durchaus erforderlich:

Es ist aber auffällig, dass der Divisor des Proportionsfaktors explizit als kleine Ziffer im Text auftaucht, der Dividend allerdings aus der Länge der "überklammerten" Gruppe gefolgert werden muss. Das führt schnell zu Problemen:

In der ersten Hälfte des obersten Taktes werden, folgend dem Gebot der Kompositionalität (b) die Triolen-Viertel ihrerseits in Triolen-Achtel aufgelöst; in der zweiten Hälfte, folgend der anderen Forderung nach kanonischer Erweiterung (a), die vier Achtel durch fünf "Quintolen-Achtel" ersetzt, die nach demselben Prinzip konstruiert sind, also leicht beschleunigt sind und die Dauer der ursprünglichen vier Achtel einnehmen.
Die zweite Zeile zeigt zur Orientierung die unbeeinflusste Standard-Abfolge der Dauernwerte.
Die dritte Zeile zeigt aber, dass die neun Anschläge von ganz oben viel näher an den (unbeeinflussten) acht Sechzehnteln liegen, als an den vier Achteln. Obwohl die Schreibweise als neun Achtel, durch zweimaliges "Triolieren", systematisch (syntaktisch und semantisch) absolut korrekt und eindeutig ist, ist es die als neun Sechzehntel-Nonolen (analog zu den fünf Achtel-Quintolen von oben!) ebenfalls. Das führt dazu, dass Achtel- und Sechzehntel-Symbole, die sich eigentlich immer um den Faktor zwei in ihrer Dauer unterscheiden, nun gleich lang erklingen!
Berühmtes Beispiel für dieses Paradox ist der Anfang der "instrumentalen Durchführung" im Finale des Liedes von der Erde von Gustav Mahler. Da notiert der Meister ab Zf. 36:

... und das ist falsch!
Es müssten natürlich Viertel-(Doppel-)Triolen sein, oder Achtel-Nonolen!
Dank einer in frühen zwanzigsten Jahrhundert eingeführten Neuerung wird die Konsistenz von Vordergrund und Mittelgrund wieder hergestellt. Dabei wird der Beschleunigungsfaktor explizit angegeben, resp. der Kehrwert des Dauernfaktors. Der Dividend wird also genauso explizit gemacht wie der Divisor:

5:4 liest man als "fünf zu vier", was heissen soll: es werden fünf von der Sorte X auf die Zeit verteilt wo sonst nur vier derselben Sorte stehen. Der Multiplikator für die Dauern ist dann 4/5, unabhängig von der Wahl von X. Diese Schreibweise ist folglich die unversellste und allemal vorzuziehen.
Mit ihr wird der Widerspruch in der ersten Takthälfte des Beispieles (X9) aufgehoben:
Auf die Achtel wird eben der Faktor 2/3 zweimal angewandt, also 4/9, auf
die Sechzehntel hingegen der Faktor 8/9. Verrechnet mit dem
Verhältnis der originalen Dauernsymbole ergibt beides die identische Dauer:
1/8 * 2/3 * 2/3 = 1/18 = 1/16 * 8/9
Die letzten beiden Notenzeilen zeigen, dass nun beide Schreibweisen
mit derselben Berechtigung und Konsistenz angewandt werden können:
4/9 * 1/8 = 1/18
Derartige "Proportionen" waren, wie oben erwähnt, in der Mensuralnotation der Renaissance tägliches Brot; ihre Kenntnis und die Fahigkeit im Umgang mit ihnen dann aber verlorengegangen. Ihr frühestes Wieder-Auftreten in der Moderne scheint uns im Zweiten Akt Siegfried: beim Auftreten des Waldvogels setzt der Komponist die Formel "9=6" dazu und braucht einen mehrzeiligen Text, um genau zu erklären, wie dies denn ausgeführt werden soll.
Wie man sieht löst diese Darstellungsweise auch ein typisches "Häufelproblem":

Ab wann wird aus einer Triole eine Sextole? (Dieses Problem auch bei [gieseking, S. 112]) Alle obigen Schreibweisen sind üblich, aber widersprüchlich! Mit der Proportionalnotation braucht man das nicht zu entscheiden, denn für rationale Zahlen gilt halt 2/3 = 4/6.
Eine andere in neuerer Zeit vorgeschlagene Notationsform ist eine n-olen Klammer, die den gesamten notierten Inhalt der n-ole überspannt, und in deren Mitte das Symbol der Dauer der Orignialmetrik steht, auf das dieser Inhalt verteilt werden soll.
Der Vorteil dieser Notation ist, dass man sofort erkennt, wie der Inhalt der n-ole als Ganzer sich in den Rest des Taktes einbettet. Der Nachteil ist, dass die herrschende Proportion erst durch explizites Aufaddieren des notierten Inhaltes und In-Beziehung-Setzen zu jenem Notensymbol errechnet werden muß.
Eine leider sehr weit verbreitete
Variante davon setzt das Zeichen der Gesamtdauer nicht alleine, sondern
nach unten in eine bruch-ähnliche Konstruktion. Oben steht dann eine einfache Zahl.
Dies ist aber eine sehr dumme Notationsform, denn diese Zahl hat keinerlei Bedeutung.
Die n-olen bisher fügen sich in den Kontext der metrischen Hierarchie ein und ersetzen nur den Teilungsfaktor genau einer Ebene lokal durch eine anderen.
Foglich gibt es im selben Sinne Duolen, und allgemeiner, n-olen mit n=2^k, wenn der ersetzte originale Teilungsfaktor eben keine Zweierpotenz ist. (Die Schreibweise als punktierte Dauer hat fast immer allerdings dasselbe rechnerische Ergebnis.)

Als nächste Komplexierungsstufe kann die n-olen Schreibweise aber auch
querständig zur Ausgangshierarchie angewandt werden.
Dabei werden also die gruppierten n Dauern der n-ole auf eine Folge
von Zählzeiten verteilt, die in der originalen Metrik nicht zusammengefasst
werden.
Dabei kann sogar eine Taktgrenze überquert werden.
(Die oberste Zeile dient nur zur Orientierung:)

In den letzten beiden Zeilen hat die zusammengefassten Folge von Dauern, auf die die drei Viertelnoten verteilt werden sollen, eine Länge von 5/8. Das aber ist keine Grunddauer, und auch keine durch Punktierung oder n-olierung erzeugbare Dauer. Nur additiv, durch Haltebögen ist diese Dauer erzeugbar, nach der Formel 1/8+1/2 oder 1/8+1/4+1/4.
(Von den in unserem Übersichtsartikel senza tempo 2012070100 --- Synopsis of Musical Notation Encyclopedias aufgelisteten Autorn weist übrigens nur E. Gould auf diese Möglichkeit hin, die aber andererseits die "synkopisch verschobenen" n-olen ausläßt. Es ist eh bemerkenswert, wie unterschiedlich die Auswahl der besprochenen Aspekte von n-olen bei den verschiedenen Autoren ist, siehe unsere Synopsen-Matrix.)
Gerade für einen solchen Fall wird manchmal die o.e. Notationsweise
"Anzahl zu Dauernsymbol" empfohlen, obwohl sie hier nicht besser ist als
oben beschrieben.
Vielmehr sollte auch hier ganz einfach die Proportion bestimmt werden, nämlich,
wie oben beschrieben, "3:2.5", d.h. die
Dauer von zweieinhalb Vierteln wird verwendet für drei Viertel.
Das Programm lilyond [lilyPond], mit dem wir die Beispiele erzeugen, kann das aber nicht verarbeiten, sondern braucht die erweiterte Form "5/6", was dieses Programm dann nur mit dem Nenner ausdruckt (die "6" in der Mitte der Klammer). Falsch ist es nicht, aber auch nicht eindeutig.
Unser Metrik-Baum kann selbstverständlich alle diese rhythmischen Phänomene als Metriken ausdrücken:
Man glaube nun nicht, dass derartige Konstrukte nur Hirngeburten avantgardistischer Theoretiker sind. Nein, gerade in romantischer Produktion können derartig querständige n-olen im Sinne einer "auskomponierten Agogik" zur Steigerung der Expressivität herangezogen werden. So in des Verfassers op. 13, Über die Dinge -- vier Lieder nach Rilke:
Der Tod ist grosz,
Wir sind die seinen,
Lachenden Mund's.
Wenn wir uns mitten im Leben meinen,

Im Rahmen der modernen Fortentwicklung der rhythmischen Möglichkeiten, sei es
in Jazz, Neuer Musik oder Elektro, können nun n-olen durchaus als eigenständige
Dauernbestimmungen verwendet werden:
Im Gegensatz zu ihrer Entstehung im Kontext von CWN, wo immer nur
z.B. drei(3) Triolen quasi "gleichzeitig" das Licht der Welt erblicken können,
indem sie zwei normale Viertel ersetzen, kann man eine einzelne Viertel-Triole
einfach als Wert "1/6" = "ein Sechstel" betrachten und ohne die Notwendigkeit einer
Dreiergruppe additiv in einen Takt einbauen.
Auf der psychischen Ebene der Produktion kann man z.B. einen Takt wie "Drei Viertel plus zwei Sechstel" relativ natürlich empfinden als "drei Viertel plus eine Viertel-Triole, deren letzes Viertel rausgeschnitten, ge-break-t, wird."
Als Taktangabe wären möglich:
3 2 9 4 13 --- + --- = --- + --- = ---- 4 6 12 12 12 |
Unabhängig von der Schreibweise ist die Mittelgrund-Struktur, gegeben als Metrik-Formel und als Baum-Diagaram ...
3*1/4 + 2*1/6
/ \
/ \
/ \
/|\ /\
/ | \ / \
1 1 1 1 1
- - - - -
4 4 4 6 6
|
Man überzeugt sich leicht das eine "rein lokale" Verwendung der Triolenproportion "3:2" auch über einer einzelnen Note genau dieselbe Bedeutung hat wie über jeder beliebig großen geklammerten Gruppen, nämlich Dauernverkürzung mit dem Faktor "2/3":

Die letzte Zeile soll, wie oben schon bei den verschiedenen Bernstein-Varianten (Abschnitt 2.9), wieder zeigen, dass die Konstruktion keinesfalls übermäßig exotisch ist: Durch Wechsel der Bezugsgröße, kompensiert durch Wechsel des Tempos, erreicht man eine viel konventionellere Notation derselben Verhältnisse.
Fassen wir unsere Ausgangsfrage und das bis hierhin Erarbeitete zusammen:
Das Problem in seiner allgemeinsten Gestalt besteht darin, eine abstrakt gegebene Folge von Ereignis- und Pausendauern (z.B. codiert als rationale Zahlen) in die korrekte Folge musikalischer Symbole zu übersetzen.
Eine bezogen auf eine gegebene Taktmetrik
sinnvolle Schreibweise einer rhythmischen Ereignisfolge ist
eine solche, die die hierarchischen Ebenen, die innerhalb des
Taktes herrschen, möglichst deutlich zum Ausdruck bringt. Dies unterstützt
das korrekte Notenlesen und Musizieren, da in metrischen Kontexten das
Zeitgefühl sich viel mehr an den metrischen Hierarchien orientiert
als an der abstrakten "berechneten" Dauer eines Ereignisses.
Diese Ausführung sollte die Notation weitgehend unterstützen.
Kriterium für die Notation ist also die metrische Hierarchie wie in
den vorangehenden Abschnitten entwickelt.
Eine mathematische Formulierung dieser Lösung ist zweckmäßig um (a) das Problem einer Rechenmaschine übergeben zu können, und (b) Diskussionen über und Vergleiche von Notationsstilen auf eine exaktere Grundlage zu stellen.
Welcher Art können nun derartige mathematische Funktionen sein? Es gibt da verschiedene, von einander weitgehend unabhängige Achsen:
Zunächst einmal kann man, ganz losgelöst von unserem konkreten Anwendungsfall, meist unterscheiden zwischen operationalen Lösungen, also Algorithmen, Rechenanweisungen, die Schritt für Schritt ausgeführt das Ergebnis liefern, und denotationellen, die als Funktion oder Logik-Formel das Übersetzungsergebnis eindeutig beschreiben, ohne eine Rezept zu dessen Konstruktion zu liefern. Letztere sind i.A. besser lesbar und verständlicher, bedienen also besser den Zweck (b), selten aber den Zweck (a).
Eine Lösung des Notationsproblems heiße lokal, wenn für eine gegebene metrische Hierarchie für jedes musikalische Ereignis (Ton oder Pause) allein aus seiner taktrelativen Anfangsposition und seiner Dauer die zu wählende Notation eindeutig bestimmt ist. Hingegen ist ein Lösung kontext-sensitiv, die darüber hinaus mehr oder weniger Information über den Inhalt des Taktes ausserhalb des zu notierenden Ereignisses kennen muss.
Ein Algorithmus ist tabellarisch, wenn für alle denkbaren Anwendungsfälle die möglichen Lösungen in Tabellen fest abgelegt, "vorverdrahtet" sind. Seine Flexibilität erhält ein solcher Algorithmus dadurch, dass der Anwender für neue Spezialfälle neue Tabellen erstellen und hinzufügen kann. Vereinfacht gesprochen kann man als Gegenentwurf dazu die regel-basierten Algorithmen sehen.
Algorithmen sind mehr oder weniger stark parametrisierbar, d.h. in ihren Entscheidungen konfigurierbar durch Einstellungen des Benutzers. Diese können durch verschiedene technische Mittel geschehen, z.B. in dem der Benutzers Ja-Nein-Schalter umlegt, oder skalare Parameter adjustiert, oder ganze Gewichtungsfunktionen definiert.
Umgekehrt kann aber auch ein automatischer Algorithmus in einem konkreten technischen Kontext Teil einer Pipeline sein, die dem Benutzer erlaubt, punktuelle Festlegungen vor Start des Algorithmus' zu treffen, oder nach dessen Lauf das Ergebnis punktuell zu überschreiben und anzupassen. Obwohl dies eine eher technologische Bestimmungsachse ist, und eher dem "tool" Kontext zugehörig, hat sie doch Einfluss auf die Flexibilität der Anwendung des Algorithmus und sollte in jede Betrachtung eingehen.
Die letzte Konsequenz in dieser Richtung löst den Algorithmus selber auf in eine Kette von Transformationen, bei denen viele kleine Schritte hintereinandergeschaltet sind, und die sogar flexibel und gemischt mit Eingriffen des Benutzers als solche konfigurierbar ist.
Mit dem nochmaligen Hinweis, dass all diese Achsen (evtl. leicht verallgemeinert) für Algorithmen im Allgemeinen gelten, weit über unsere konkrete Anwendung hinaus, wenden wir uns nun den konkret existierenden Lösungen zu:
Die zu Beginn erwähnten Algorithmen von Byrd in [byrd] und Gieseking in [gieseking] basieren auf der Definition eines "metrischen Gewichtes" (bei ersterem "rhythmic strength"), welches allen rationalen Zeitpunkten relativ zur Taktdauer zugeordnet wird.
Die Notationssoftware lilyond [lilyPond] beinhaltet einen tabellen-basierten Algorithmus zur Balkensetzung.
Diese Lösungen werden nun genauer dargestellt, diskutiert und kritisiert.
Beide gewichtsbasierten Algorithmen gehen aus vom rezeptionspsychologischen
Modell von Metrik als überlagerten Rhythmen:
Demzufolge werden beim Ablauf des musikalischen Inhaltes eines Taktes
die ineinander geschachtelten Teilungsebenen
der Metrik, wie oben entwickelt, als
parallel ablaufende, gleichsam "intern-polyphone" Ereignisfolgen oder
Schwingungen empfunden.
Jeder Zeitpunkt des Taktes, repräsentiert durch eine rationale Zahl,
erhält als Gewichtsmaß die Anzahl derartiger Raster zugeordnet, in denen er auftritt.
In Beispiel eines konventionellen 12/8 Taktes also
1/1 x
1/2 x x
1/4 x x x x
1/12 x x x x x x x x x x x x
Gewicht:
4 1 1 2 1 1 3 1 1 2 1 1
Zeitpunkt:| | | | | | | | | | | |
0 | | | 1/3 | | 2/3 | | |
1/12 | 5/12| | 3/4 |
1/6| 1/2 5/6
1/4 7/12 11/12
|
Ausgehend von dieser Gewichtsfunktion 10 werden nun Regeln definiert für
"(Notationelle) Zerlegung" bedeutet dabei die Bestimmung aller takt-relativen Zeitpunkte, an denen für das Klang- oder Pausen-Ereignis (gegeben durch takt-relativen Startpunkt und Dauer) ein neues Notensymbol erscheinen soll. Im Falle eines Klang-Ereignisses wird dieses an das Vorgänger-Symbol mit einem Haltebogen angebunden. Dadurch sind unmittelbar auch die Dauern der einzelnen zu setzenden Symbole festgelegt.
Die Regeln für die Zerlegung von Dauernwerten klingender Ereignisse sind bei beiden Autoren weitgehend identisch:
Diese Regeln werden rekursiv angewandt, d.h. eine "Zerlegung" erzeugt zwei Dauernwerte, deren erster allemal notiert wird und mit dem Folgewert mit einem Haltebogen (s.o. Abschnitt 3.1) verbunden wird. Der zweite hingegen wird wieder nach diesen Regeln auf Zerlegung überprüft.
Die letzte dieser Regel ist schwer zu finden, aber unverzichtbar, und ihre Herausarbeitung die wichtigste Leistung in diesem Abschnitt von [gieseking]. Man beachte, dass sie als einzige nach obiger Definition nicht lokal ist!
Zerlegung von Pausen wird nur von Gieseking explizit behandelt. Seine Regeln lauten ...
Zusätzlich führt Gieseking eine Regel an, die auf dem Endergebnis der rekursiven Anwendung dieser Schritte arbeitet und zerlegte Pausen wieder verschmilzt:
Wir halten diese Regeln und ihre Konsequenzen für durchaus diskussionswürdig
in dem Sinne, dass hier parametrisierbare Regeln die
praktische Wirklichkeit besser abbilden würden.
Obige Version erlaubt z.B. keinerlei punktierte Pausen, ausser zur Auffüllung einer
vollständigen Dreier-Einheit der expliziten Taktmetrik (also im
von uns so genannten "mittleren Organisationsbereich").
Für diesen Kontext ist auch die Regeln Nr. 2 gedacht. Gieseking
meint entdeckt zu haben, dass Viertelpausen im Sechs-Achtel-Takt
oder Halbepausen im Sechs-Viertel-Takt generell verboten sein sollen, und dazu
soll diese Regel dienen.
(Sie ist allerdings unvollständig, da sie auch dazu führt, dass in einem
Vier-Viertel-Takt eine Achtelpause auf der Eins zerlegt wird in zwei Sechzehntel !-)
Die Partitur des Rheingold z.B. verfährt hingegen genau entgegengesetzt:
Pausiert die ganze erste Hälfte des Sechs-Achtel-Taktes, so steht dort eine
Viertel gefolgt von einer Achtel-Pause, also genau jene Zweier-Zusammenfassung
die Gieseking ausschließt. Nie aber steht dort eine punktierte Viertel!

Der Verfasser hingegen liebt es, Pausen zu punktieren, und tut dies zwar mit mehr Zurückhaltung als mit klingenden Noten, prinzipiell aber sowohl als Bestandteil von positiven wie von negativen Punktierungen.
Die Formulierung der Pausen-Regeln ist also in der Tat komplexer als man meint, es existiert keine eindeutige Lösung, und die Formulierung der verschiedenen Alternativen scheint sich durchaus aufwendig zu gestalten. Umso erstaunlicher, dass dieses Thema "in keiner der gängigen Allgemeinen Musiklehren behandelt wird" [gieseking, S. 115].
Balkensetzung wird ebenfalls nur in [gieseking] explizit behandelt. [byrd] bringt nur einen aufwendigen Algorithmus zur Bestimmung der Richtung von Teil-Balken ("Balkenstückchen"), basierend auf metrischen Gewichten, den der spätere Autor aber als überflüssig bezeichnet.
Dort findet sich stattdessen eine einfache Regel für die Richtung der Teil-Balken, und ein Algorithmus zur Abtrennung von Balkengruppen.
Die explizit aufgelisteten und inferierbaren Eigenschaften von dessen Ausgabe sind eine wertvolle Checkliste, und Katalog für mögliche Parametrisierung:
Diese Regeln sind durchaus kritisch zu sehen. So bringen sie die erste Zeile des folgenden Beispiels hervor, obwohl in vielen Stilen die Schreibweise der zweiten Zeile die bessere wäre:

Auch weist der Autor darauf hin, dass die Forderung nach mindestens zwei "leichteren" Anschlägen pro Balkengruppe zu-kleine Gruppen vermeiden soll, wie die ersten beiden Zeilen des folgenden Beispiels zeigen, dass aber evtl. die kleinere Gruppengröße genau die gewünschte sein kann, wenn die Binnenstruktur wechselt, siehe Zeile drei. Diese Differenzierung bedürfte wieder einer typischen nicht-lokalen Regel!

Teil-Balken am Rande der Balkengruppe sollen immer nach "innen" zeigen. Alle innenliegenden nach links, wenn eine schwerere Zählzeit folgt, sonst nach rechts.
Diese einfache Regel gälte aber nicht mehr in modernerem Bebalkungs-Stil, wenn nämlich Pausen in die Bebalkung integriert werden, sei es durch Verlängerung der Balken extra für eine Pause, oder auch nur durch Überbalkung im Falle einer von Ereignissen umrahmten Pause. Eine Achtel- gefolgt von einer Sechzehntel-Note gefolgt von einer Sechzehntel-Pause könnte dann mit zwei Teil-Balken enden, die beide nach aussen zeigen, auf die Pause hin, und diese so virtuell in die Balkengruppe inkludieren:

Alle strategischen Entscheidungen zur Pausen-Integration müssten eh Gegenstand von Parametrisierung sein.
Würdigung und Vergleich beider Arbeiten:
Die besprochenen Kapitel beider Arbeiten sind wertvolle Beiträge, in denen grundlegende Fragen der musikalischen Orthographie zum ersten Male einer stärker mathematisch orientierten Modellierung unterworfen wurden. Dass sie wie alle Pionierarbeiten unvollständig und verbesserungswürdig sind, scheint notwendig.
Für unsere eigene Forschungs- und Programmiertätigkeit bilden sie wertvolle Vorarbeiten, die u.a. ein genaues Verorten von Varianten, Entscheidungen und Parametrisierungen sehr vereinfachen.
Zumeist sind die Erweiterungen Giesekings gegenüber Byrd
durchaus richtig und wichtig, besonders die letzte Regel zur Synkopenspaltung,
s.o.
Manche Modifikationen sind allerdings Verschlimmbesserungen:
Bei Byrd ist das metrische Gewicht für eine gegebenen Taktart einmal
festgelegt.
Gieseking meint nun das ursprüngliche Verfahren zu verbessern,
indem er dieses induktiv herleitet (S. 104):
Er bildet die größte gemeinsame Dauer aller irgendwo im Takt auftretender
n-olen, und definiert das metrische Gewicht durch die Überlagerung aller sich
derart ergebender möglicher Raster.
Darüber hinaus ersetzt er die ursprünglich von null an abwärts gehende
Zählweise durch positive Zählung.
Dies erscheint uns eine Verschlechterung: Die ursprünglich rein lokale Entscheidung wird ersetzt durch eine stärker kontext-sensitive: Treten im zweiten Viertel (wie in seinem Beispiel) Quintolensechzehntel auf, so werden die in die ("globale") Gewichtsfunktioni des gesamten Taktes erst eingerechnet, fallen aber bei all den Takt-Teilen, in denen sie im Rhyhthmus garnicht präsent sind, durch o.e. Regeln wieder heraus.
Man könnte argumentieren, dann sei doch kein Schaden entstanden.
Aber ein Algorithmus, der zwar das richtige Ergebnis liefert, aber dabei
die kausalen Strukturen der anzuwendenden Begrifflichkeiten
nicht abbildet, bleibt philosophisch doch unbefriedigend.
Die Konstruktionsregel, diese n-olen nach abnehmendem Teilungsfaktor
geordnet in das metrische Gewicht einzuarbeiten ist z.B. eine
völlig beliebige.
Ebenso beliebig ist es, den Takt (in seiner Rolle als Dauer)
überhaupt zum Regulator dieser Zusammenfassung zu machen.
Grundlage jedoch all dieser Verschlechterungen ist es, dass der Sinn
der negativen Zählrichtung nicht respektiert wurde: Sie nämlich macht die
o.e. Regelsammlung bei Byrd zu einer jederzeit
lokal transparent erweiterbaren, ohne dass zunächst
ein Takt als ganzer erst vollständig durchgerechnet sein müsste.
Mangel beider Verfahren ist, dass zwar "korrekte Zerlegungen"
bereits notierter Dauern behandelt werden, nicht aber das viel
allgemeinere Problem, einen ganz ohne Notation gegebenen Dauernwert
des Mittelgrundes (z.B. codiert als rationale Zahl)
überhaupt erst in eine Notation zu übersetzen.
Dem entspricht vice versa, dass zwar von "eventuell nicht
darstellbaren Rest-Dauern"
und "maximalen Wertpunkten" geredet wird, deren Problematik aber
von der der metrisch korrekten Darstellung abgetrennt
und in Nebensätzen als trivial lösbar behauptet wird.
13
Das ist falsch.
Dass eine 15/16 nicht als dreifach punktierte Halbe dargestellt wird, ist
über den eindimensionalen Parameter "maximal erlaubte Punktierung" einstellbar.
Ob aber eine punktierte Halbe mit angebundender punktierter Achtel
die bessere Darstellung als eine Halbe mit doppelt punktierter Viertel ist,
wagen wir ohne Kenntnis der gemeinten Metrik nicht zu beurteilen.
Die Notensatz-Software lilypond ist "open source", so dass ihre Algorithmen nachvollziehbar und teilweise auch als solche dokumentiert sind.
Das Programm (in der Version 2.14.xx) besitzt keinerlei Funktion zur automatischen Zerlegung oder Darstellung von Dauernwerten. Vielmehr gibt der Benutzer explizit die Folgen der Dauernwerte an, einschliesslich Haltebögen, etc. Hingegen verfügt es über Automatismen zur Bebalkung, die durchaus betrachtenswert sind.
Zunächst einmal kann durch Anhängen der eckigen Klammern an
Notenwerte der Anfang und das Ende einer Balkengruppe explizit
definiert werden, oder durch ein Kommando \noBeam die Fähnchen-Darstellung
erzwungen. Beides nennt sich "manual beams".
Nur diese können Pausen überspannen, resp. anschliessen.
Darüberhinaus kann für jeden Notenhals die Anzahl der links und rechts
ansetzenden Balken explizit überschrieben werden.
Gleichzeitig gilt aber dennoch eine Teil-Automatik: Die Anzahl der Balken
wird aus der Dauer der Noten errechnet. Eventuelle Unterteilungen
durch Unterbrechungen der Bebalkung orientieren sich an der Dauer des
"beats" (i.e. Zählzeit) und sind explizit an- und abschaltbar.
% ...
\set subdivideBeams = ##t
\set baseMoment = #(ly:make-moment 1 8)
c'16[ c' c' c' c'32 c' c'16 c' c'32 c']
% ...
|
...liefert an der Achtelgrenze geteilte Balkengruppen...
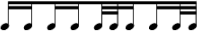
Demgegenüber sind "automatic beams" errechnet aufgrund eines mehrstufigen Parametrisierungsmechanismus. Grundlage sind die Werte baseMoment und beatStructure, die ungefähr unserer nominellen und mentalen Zählzeit entsprechen. Letztere ist eine Liste von natürlichen Zahlen, welche unmittelbar die zu bebalkenden Gruppen angeben, gemessen in der ersteren.
Weiterhin kann mit beatExceptions eine Abbildung von "Dauer zu Zeitpunktliste" angegeben werden, die für alle Gruppen, welche genau diese Dauer als kürzeste enthalten, angeben, an welcher taktrelativen Position diese Gruppe zu enden hat. Damit kann das in [gieseking] durch dynamische Regeln angestrebte Ergebnis auf tabellarischem Wege erreicht werden. So kann z.B. festgesetzt werden, dass "Nur-Achtel" in Vierergruppen verbalkt werden, Sechzehntelgruppen aber in kleineren. Folgendes Beispiel ist artifiziell, als es letztere in beiden Takthälften unterschiedlich behandelt:
% ...
\time 4/4
%% dies stellt die DEFAULTS her, danach überschreiben:
\set Timing.beamExceptions =
#'(
(end .
(
((1 . 8) . (4 4))
((1 . 16) . (4 4 8))
)))
c'8 c' c' c' c' c' c' c'
| c'8 c'16 c'16 c'8 c'16 c'16 c'8 c'16 c'16 c'8 c'16 c'16 |
% ...
|
...liefert diese Balkengruppen...

Für jede "Taktart-Angabe" können diese drei verschiendenen Einstellgrößen vordefiniert sein; wann immer die Taktart frisch angewählt wird, werden diese zu den aktuellen gemacht, bis sie explizit überschrieben werden.
Interesssant, wie flexibel und ausdrucksfähig diese einfache tabellarische Methode ist.
Während verständlicherweise weitestgehende Lokalität (im Sinner der Definition oben in Abschnitt 3.2) bei jedem Lösungsvorschlag anzustreben ist, gibt es wenige Notationsprobleme, die durchaus nicht-lokaler Natur sind, die also nicht entschieden werden können ohne sich größere Kontexte anzusehen.
Gieseking konstruiert folgendes Beispiel, nach den Angaben von Chlapik, [chlapik, S. 52]:
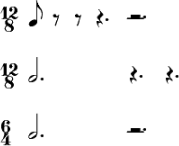
In der ersten Zeile kann die zweite Hälfte des Takts problemlos durch eine
einzige Pause dargestellt werden.
Um das Metrum des Taktes zu klären, dass also auf einen Blick
sichtbar ist, dass es sich um 12/8 und nicht um 6/4 handelt, reicht
die erste Takthälfte.
In der zweiten hingegen muss die Pause zu genau
demselbem Zwecke aufgelöst werden!
(Der Vergleich mit Zeile drei zeigt, dass die hierarchische Schichtung
der Teilungen sonst nicht erkennbar wäre.)
Ein anderes Beispiel: Die erste Zeile zeigt Takt 137 f. der ersten Violinen aus dem Adagio von Bruckners Dritter in der ersten Fassung, so wie in der Gesamtausgabe Band III/1 tatsächlich gestochen!

Die die Taktmitte synkopisch überspannenden Achtelnoten b' und ges'' werden also (vom hochprofessionellen Notenstecher dieser Ausgabe und von den wissenschaftlichen Herausgebern!) als gut lesbar angesehen, wenn sie Bestandteil einer durchgehenden synkopischen Folge sind.
Hingegen, wie die zweite Zeile zeigt, sind dieselben Noten von Pausen umgegeben orthographisch allemal ungewöhnlich, wenn nicht gar als falsch zu bezeichnen.
Zeile drei zeigt, dass die Pausen sogar so bleiben könnten, wenn nur die Synkope, die ja die alleroberste Taktteilung betrifft, explizit gemacht wird.
Um all diese Beschränkungen aufzuheben, und um mit lokalen, taktübergreifenden, und spontan definierten Metriken die Menge des Behandelbaren, zumindest potentiell, deutlich zu erweitern, planen wir im Rahmen von tScore einen andersartigen Algorithmus, basierend auf Muster-Suche in Graphen.
Die anzuwendenden Grundregeln sind hingegen selbstverständlicherweise sehr ähnlich zu denen der zitierten Autoren, deren Bedeutung für unsere Arbeit nicht zu überschätzen ist. Andererseis soll unser Algorithmus deutlich über das oben Vorgestellte hinausgehen, als die Graphen, die die Metriken repräsentieren, "selbst-modifizierend" agieren können, wenn spontan auftretende "krumme" Werte lokale Metriken erfordern, ein Problem dass die Vorgängerautoren ausklammern mussten.
|
[musixtex]
und und MusiXTEX Using TeX to write polyphonic or instrumental music the web, 2002 http:///ftp.gwdg.de/pub/ctan/macros/musixtex/doc/musixdoc.pdf |
|
[mggprisma]
Notation Anderas Jaschinski(Hrsg.) Bärenreiter, Kassel, 2001 ISBN 3-7618-1625-1 |
|
[byrd]
Music Notation By Computer Indiana University, Bloomington, 1984 |
|
[wanske]
Musiknotation -- Von der Syntax der Notenstichs zum EDV-gesteuerten Notensatz Schott, Mainz,, 1988 ISBN 3-7957-2886-X |
|
[chlapik]
Die Praxis des Notengrafikers Doblinger, Wien, München, 1987 ISBN 3-9000-035-96-2 |
|
[gieseking]
Code-basierte Generierung interaktiver Notengraphik Universität Osnabrück, Osnabrück, 2000 ISBN 3-923486-30-8 |
1 So ist z.B. ein ärgerlicher Entwurfsfehler in lilypond, dass die Dauer von unvollständigen Takten (mittels "\partial") und von ganztaktigen Pausen (mittels "R") mit der Vordergrund-Struktur der Notendauer (also als evtl. punktierte Noten-Grunddauer) anzugeben ist. Benötigt würde aber eine Angabe als Rationale Zahl, aus dem Mittelgrund; einzig dies ermöglicht dort Dauern wie 5/8!
2 Wobei Notation ja immer bedeutet nicht nur ein System des Aufschreibens, sondern auch, ja vielmehr noch, eines des Denkens!
3 Selbst dieser fundamentale Satz ist einzuschränken wegen der "Brahms-Punktierung". Aber auch ohne diese bezieht er sich stets auf die Mittelgrundstruktur und gilt nicht unbedingt in der sichtbaren Vordergrundgestalt dieser "Stimme", wegen möglicher "unsichtbarer" und "gemeinsamer" Pausensymbole.
4 Im Zusammenhang mit komplexeren Metriken mit wechselnden Grundschlägen ist zu beachten dass die hier auf unterster Ebene auftretenden rationalen Zahlen pure quantitative Angabe der Dauer sind, und keine Strukturaussagen! Ein Grundschlag wie "3/16" oder gar "5/32" würde also implizit, wie jeder andere, wie erwähnt immer nur durch zwei(2) geteilt, also in 3/32, 3/64, etc., resp. 5/64, 5/128, etc.
5 Wir werden in Kürze allerdings auch "5*3" ausnahmsweise als "einfache Folge" zulassen!
6 Benannt allerdings als "9/16" mit weggelassener Triolen-Klammer.
7 Um die Notensymbole anzuzeigen muss ein Darstellungs-Font installiert sein für den Unicodebereich U1D180 ff.
8 Meist wird der Aufteilungs-Vorgang selber, oder die aus drei aufeinander folgenden "Triolen-Vierteln" bestehende Gesamtstruktur als "Viertel-Triole" bezeichnet. Die Benennung "Viertel-Triole" ist aber auch für ein einzelnes "Triolen-Viertel" durchaus üblich.
9 Es gibt allerdings moderen Erweiterungen von CWN, die das durchaus ermöglichen.
10 Es findet bei beiden Autoren noch eine Nach-Modifikation statt. Zur Verstärkung der Trennwirkung von Dreiergruppierungen, so sie in der Taktart benannt sind, wird deren "eins" doppelt gezählt. Im obigen Beispiel hieße die Gewichtsfolge also 5 1 1 3 1 1 4 1 1 3 1 1. Dies wird allerdings für Pausen nicht angewandt.
11 Dieses "andernfalls" vermuten wir nur als anzuwendenden Konjunktion, denn keiner der beiden Autoren äußerst sich präzise zu der Priorisierung der Regelsammlung!
12 Deshalb, weil es heisse "vier gleichwertige Pausen können in einem Takte niemals nebeneinander stehen", bei Hader, 1948, welches uns aber leider nicht vorliegt.
13 Gieseking behauptet, dass seine Abbildung 4.5, ein veraltetes Flußdiagramm mit globalen, nicht deklarierten und kaum lesbaren Variablen, sei "ein kleiner Algorithmus, der den Zähler eines beliebigen Notenwertes gemäß maximal erlaubter Punktierung in kleinere Summanden zerlegt." Derartiges ist nur geeignet, Leser, die nicht wissen, was ein sauber geschriebener Algorithmus ist, zu beeindrucken, und alle anderen abzuschrecken. Überhaupt sind viele seiner Formeln mehr "for show" hingeschrieben, als dass sie wirklich etwas bedeuteten oder gar fehlerfrei wären. Schade.
©
senzatempo.de
markuslepper.eu
2019-12-20_20h44


produced with
eu.bandm.metatools.d2d
and XSLT
music typesetting by musixTeX
and LilyPond