Fraktalität ist eine Eigenschaft von mathematischen Objekten, welche Ende des vor-vorigen Jahrhunderts entdeckt wurde, und in den Sechziger/Siebziger Jahren des vorigen zu wirklicher Populärität gelangte.

Im Zuge dessen fanden fraktale Gestaltungsprinzipien auch Eingang in bildende Kunst, Musik, ja, Literatur.

Dieser Artikel soll nur so knapp wie möglich einen Eindruck vom Grundprinzip vermitteln, --- es gibt eine Fülle von auch allgemeinverständlicher Darstellungen, die hier keinesfalls vermehrt werden soll. (Dieses Erklärungsmuster wurden dem Verfasser zuerst präsentiert durch einen ausgezeichneten, anschaulichen, gut nachvollziehbaren und sehr unterhaltsamen Vortrag von Dr. Heinz-Josef Florian, 19950126 als Gastvortrag an seiner damaligen Hochschule. Diesem gebührt also die eigentliche Verfasserschaft an den folgenden Inhalten und alles Lob für deren Darstellung !-)

Fraktalität wird oft mit "Selbstähnlichkeit" gleichgesetzt. Dabei soll Selbstähnlichkeit bedeuten, dass ein Ganzes "ähnlich" ist wie die Teile, aus denen es zusammengesetzt ist. Es muss aber zur einfachen Selbstähnlichkeit etwas hinzukommen, damit von Fraktalität im engeren Sinne geredet werden kann. Dieses, was hinzukommen muss, ist durchaus substantiell, und genau davon soll im folgenden ein wenn auch oberflächlicher so doch präziser Eindruck verschafft werden.

Nehmen wir eine beliebige geometrische Figur, z.B. eine Strecke einer bestimmten Länge L, wie in Abbildung (A). Verkleinern wir diese um einen Faktor f, errechnen die neue Länge also zu L*(1/f).

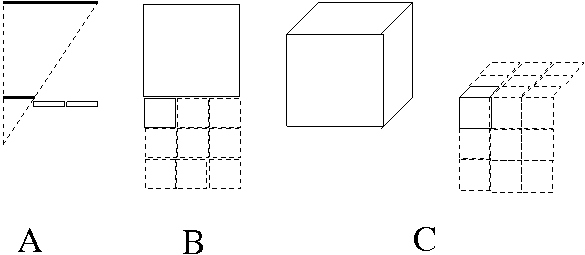
Fasst man die kleinere Strecke als einen Bestandteil der größeren auf, so gilt in diesem Verhältnis zweifellos "Selbstähnlichkeit" wie oben beschrieben: die lange Strecke sieht genauso aus wie die kurze, nur verkleinert, und besteht aus mehreren Abschnitten, die als Kopien der kurzen Strecke aufgefasst werden können.

Fragen wir uns dann, wieviel Male das Verkleinerte in das Original hineinpasst, und nennen diese Zahl n, so gilt hier offensichtlich n=f, das dreifach verkleinerte passt dreimal in das Original. Genauso würde das fünffach verkleinerte fünfmal hineinpassen.

Bei einem Quadrat (Abbildung B) ist das schon anders: das zweifach verkleinerte passt viermal hinein, das dreifach verkleinerte neunmal, das vierfach verkleinerte sechzehnmal, etc.

Ein doppelt verkleinerter Würfel (Abbildung C) passt acht Mal in den Originalwürfel. ein dreifach verkleinerter siebenundzwanzig Mal.

Es gilt also allgemein
n = f ^ d.
Im ersten Fall gilt d=1, im zweiten d=2, im dritten d=3. Die Zahl d nennt man in diesem Zusammenhang Dimension. ¹

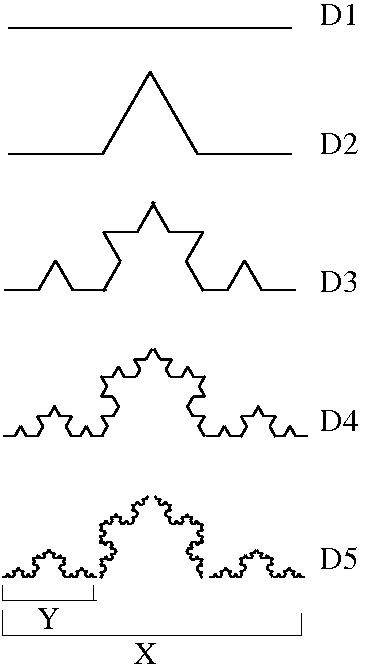
Konstruieren wir nun eine andere Figur wir folgt: Wir nehmen eine Strecke einer bestimmten Länge (Abbildung D1). Das mittlere Drittel entfernen wir und ersetzen es durch eine "Zacke", die genau zwei Stecken dieser Länge einfügt. (Wir erhalten also vier Strecken von der Länge eines Drittels der Anfangsstrecke, Abbildung D2)

Genau dasselbe machen wir nun mit jeder dieser vier Strecken, und erhalten Abbildung D3.
Es ergeben sich sechzehn Strecken, auf die wir wiederum diese Transformation anwenden.
Und das tun wir wiederum auf das Ergebnis, und zwar unendlich oft.
(Was immer das auch heißen soll. Es wird aber im folgenden unverzichtbar, dass dies "unendlich oft" geschieht!-)

Vergleichen wir "danach" (also nach den unendlich vielen Konstruktionsschritten!-) das sich ergebende Gesamtgebilde X mit dem, was aus dem ersten Drittel der Anfangsstrecke geworden ist Y. Dann ist der Verkleinerungsfaktor von X nach Y zweifellos gleich drei. Das kleinere Gebilde passt aber VIER-mal in das Gesamtgebilde hinein. Was gilt nun für die Dimension, die in diesem Falle D heißen möge? Behalten wir die allgemeinen Definitionen von oben bei, setzen die konkreten Zahlenwerte dieses Beispiels ein, und formen um, mit Hilfe von Logarithmen:
f=3
n=4
n = f ^ d
4 = 3 ^ D
ln 4 = ln (3^D) = (ln 3)*D
D = ln 4 / ln 3 = 1.3862944.. / 1.0986123.. = 1.2618595..

Für die Dimensionalität (wie oben definiert) unseres Gebildes erhalten wir keine ganze Zahl, sondern einen unendlichen, nichtperiodischen Bruch, eine "Fraktion". Deshalb der Name "Fraktal" für die oben konstruierte Gestalt, und alle ähnlichen.

Es ist übrigens entscheidend, dass der Konstruktionsprozess "unendlich oft" durchgeführt würde. Nehmen wir an, wir würden es nur tausend Mal machen. Dann hätte die Gestamtgestalt X tausend Ebenen dieser Zacken-Vorsprünge, und also auch ihre Verkleinerung.
Das aus dem ersten Drittel der Ursprungsstrecke hervorgegangenen Teilstück der Gesamtgestalt Y hätte aber nur neunhundertneunundneunzig. Also wäre es mitnichten eine Verkleinerung der Gesamtgestalt, und schon die einfache Selbstähnlichkeit wäre garnicht gegeben. Es ist also fundamental, dass der Konstruktionsprozess "beliebig oft" abläuft, oder auch "unendlich oft".

(Deshalb kann man das Ergebnis auch nicht zeichnen! Nur Annäherungen an das Ergebnis können gezeichnet werden, um die wirkliche fraktale Struktur auch auf dem Papier zu konstruieren bräuchte man -- unendlich lange !-)

Besonders popularisiert wurden Fraktale in den Siebziger Jahren durch Benoît B. Mandelbrot [mandelbrot].

Die Pionierarbeit wurde von ca. 1890 bis 1930 durchgeführt, und i.A. nennt man Weierstrass, Cantor, Hausdorff, Bolzano, Koch (der Erfinder unserer obigen Kurvenkonstruktion, der "Kochschen Schneeflocke), Sierpiński, und andere "Giganten" (Mandelbrot!-)

Seitdem gibt es wunderschöne Visualisierungen, besonders seit der Weiterentwicklung der Computertechnik in den Achtzigen, und auf "YouTube" etc. finden sich heutzutage viele Beispiele von "Julia-Mengen", Kamerfahrten tief in ihre Unendlichkeit, bunt gefärbte Schneeflocken etc. Wie immer sind die deutsch- und englischsprachigen Wikipedia-Artikel ein guter Startpunkt, so dass sich weitere Quellenangaben hier erübrigen.

¹ Die auf diese Art definierte Dimension heißt "Haussdorff-Dimension" . FIXME

© senzatempo.de     markuslepper.eu       2019-10-26_20h43          
produced with eu.bandm.metatools.d2d    and   XSLT
music typesetting by musixTeX    and   LilyPond