^phaenomen

Der Goldene Schnitt

Natürliche Grenze und immanente Grenzüberschreitung

1 Der Goldene Schnitt als Algebraisches und Geometrisches Phänomen

1.1 Definition und Berechnung

Wenn auch das "Überdauern des Schlußstriches" im Werke J.S. Baches selten so explizit komponiert wird, wie für die cis-moll-Fuge/WKI nachweisbar (siehe senza tempo 1.1), so ist es doch fast allen Sätzen Bachs immanent durch die gewöhnlich anzutreffende metrische Gliederung im Verhältnis des Goldenen Schnittes (im folgenden kurz "GS").

Auch dort, wo andere Proportionen die konstitutive, hauptsächlich wirksame und wahrnehmbare Gliederung bilden, wird sich auf sekundärer oder tertiärer Ebene stets der GS nachweisen lassen.

Der GS ist bekanntlich die Teilung einer gegebenen Größe in zwei, so, daß der größere Teil $b$ zum kleineren $a$ sich verhält wie das Ganze $(a + b)$ zum größeren $b$ .

Setzen wir $a = 1$ , so erhalten wir als $b$ den "Vergrößerungssfaktor" des GS, welchen wir im folgenden $beta$ nennen, durch die Gleichungen

\begin{matrix} es gilt & b / a & = & (a + b) / b \\ oder auch & beta / 1 & = & (1 + beta) / beta \\ ergo & {beta}^{2} & = & 1 + beta \\ ergo & {beta}^{2} - beta & = & 1 \\ ergo & {beta}^{2} - beta + 1 / 4 & = & 5 / 4 \\ ergo & {(beta - 1 / 2)}^{2} & = & 5 / 4 \\ ergo & beta - 1 / 2 & = & \sqrt{5 / 4} \\ ergo & beta & = & \sqrt{5 / 4} + 1 / 2 \\ ergo & beta & = & \sqrt{5} / 2 + 1 / 2 \\ ergo & beta & = & 1.618034 ... \end{matrix}

Diese irrationale Zahl ist die gesuchte Proportion.

1.2 Geometrische Konstruktion

Nennen wir das gegebene Ganze $c$ , so ergibt sich eine einfache geometrische Konstruktion seiner Teilung durch den Ansatz ...

\begin{matrix} b / c & = & (c - b) / b \\ ergo & b^{2} & = & c^{2} - b c \\ ergo & b^{2} + b c + {(c / 2)}^{2} & = & c^{2} + {(c / 2)}^{2} \\ ergo & {(b + c / 2)}^{2} & = & c^{2} + {(c / 2)}^{2} \end{matrix}

was eine schöne "rückwärtsgerichtete" Anwendung des berühmten "Satzes des Pythagoras" erlaubt:
geometrische Konstruktion des Goldenen Schnittes

Eine zweite, direkt aus dieser Abbildung folgende Konstruktionmethode ist diese:

Man stelle sich in die Mitte eines kreisrunden Platzes.
Man denke sich ein darin eingeschriebenes Yin-und-Yang-Symbol und entscheide sich für einen der beiden Halbkreise.
Man bestimme den Punkt "x", wo der die beiden Halbkreise trennende Durchmesser des Platzes dessen Peripherie trifft, auf der Seite des gewählten Halbkreises.
Nun gehe man seinem Halbkreis nach.
Sobald man genau zwischen dessen Mittelpunkt "m" und jenem Punkt x ist, teilt man diese Strecke im G.S.

Konstruktion des Goldenen Schnittes mittels Yin und Yang

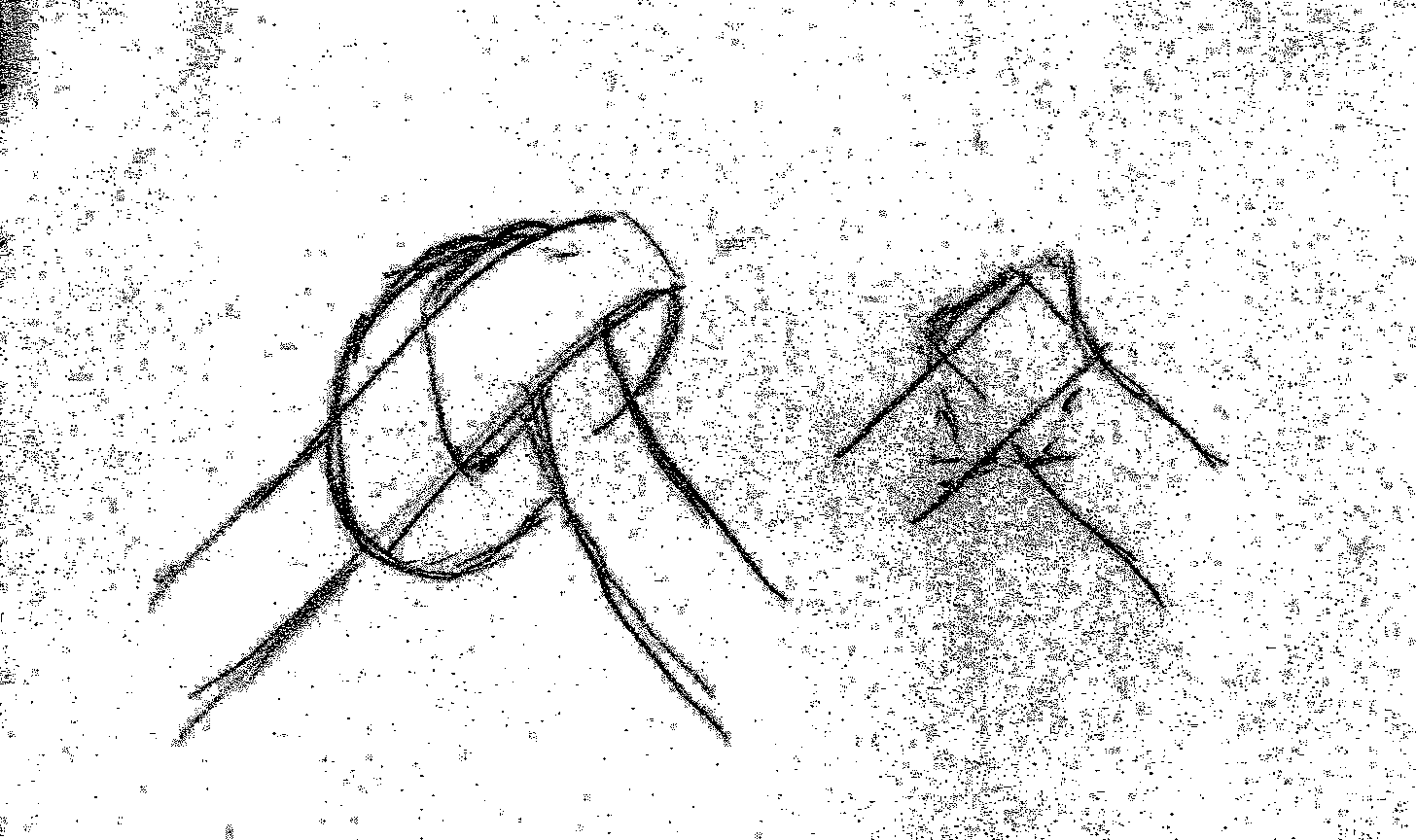
Oder etwas einfacher: Man mache einen Knoten in ein flaches Papierband: Konstruktion des Goldenen Schnittes mittels Knoten

1.3 Die grundsätzlich unbegrenzte Fortsetzbarkeit

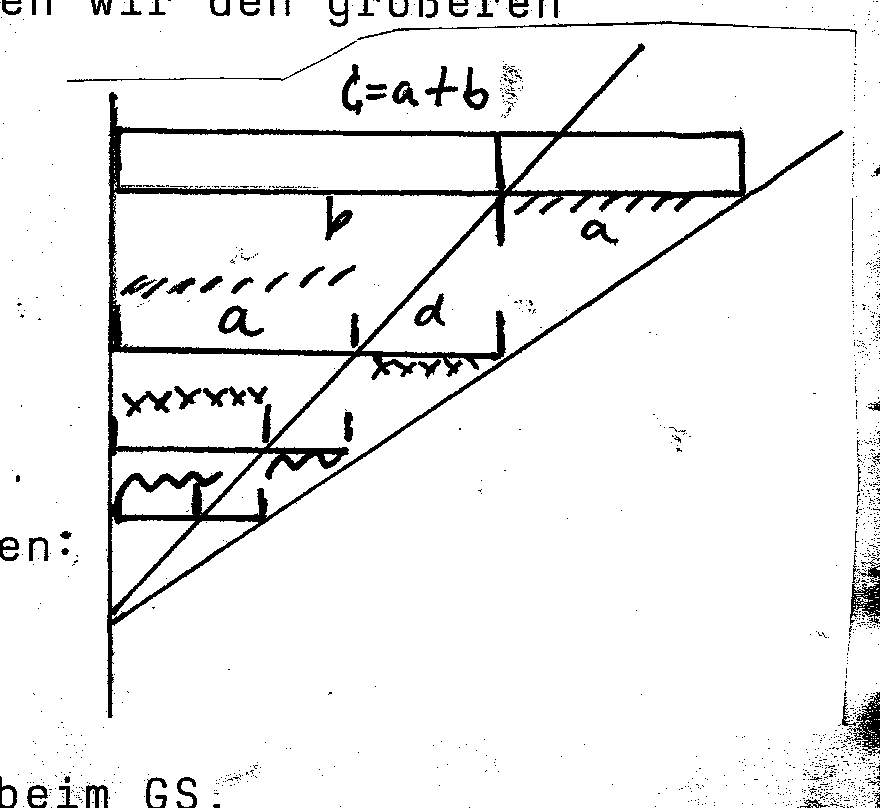
Da nun das Verhältnis des größeren Teiles $b$ zum kleineren Teil $b$ (laut Definition!) dem des Ganzen zum größeren entspricht, also eben auch $= beta$ ist, so können wir den größeren Teil $b$ seinerseits zusammengesetzt aus dem kleineren $a$ und einem Rest $d$ betrachten.
Was eben "Innenverhältnis" $b / a$ war, ist nun Außenverhältnis $(a + d) / a$ .
Auch dies "neue" Außenverhältnis entspricht der Proportion $beta / 1$ : Lt. Definition des GS. gilt dies nun auch für das neue Innenverhältnis.
Wir falten die Proportion quasi nach innen:

\frac{d}{a} = \frac{b - a}{a} = \frac{a}{b} = \frac{b}{a + b}

Punktrechnung und Strichrechnung fallen beim GS. zusammen:

beta - 1 = 1 / beta

Fortsetzung der Teilung im Goldenen Schnitt nach innen

1.4 Annäherung durch die Fibonacci-Folge

Eine ganzzahlige Annäherung des GS bietet die FIBONACCI-Folge) bei der jede Zahl die Summe ihrer beiden Vorgänger ist :

1   
    2 
1 + 2 = 3 
    2 + 3 = 5 
        3 + 5 = 8 
            5 + 8 = 13 
                8 + 13 = 21 
                         ... 34 55 89 144 233 etc.

Die Verhältnisse zweier Glieder dieser unendlichen Folge nähern sich dem GS zunehmend an.
Z.B. ist 233 / 144 = 1.6180556~ß.
Die Fibonacci-Folge spielt in der Musik von jeher, in allen Stilen und Epochen, eine große Rolle.
Man betrachte z.B. folgende Tonhöhenstrukturen.
Deren erste, die sog. "ballistische Kurve" beschreibt interessanterweise zwei verschiedene Dominantseptakkorde, G7 und (man lese h als ces) Des7:

2 Exkurs zu Pentagramm und Pentagon

Seite und Diagonale des regelmässigen Fünfecks verhalten sich zueinander im Goldenen Schnitt.

Der Beweis dieses Satzes ist eine interessante Demonstration "geometrischer Evidenz"; seine Anwendung ermöglicht eine anschauliche Darstellung der Irrationalität des GS-Faktors ß.

2.1 Der Goldene Schnitt in den Seitenverhältnissen von Pentagramm und Pentagon

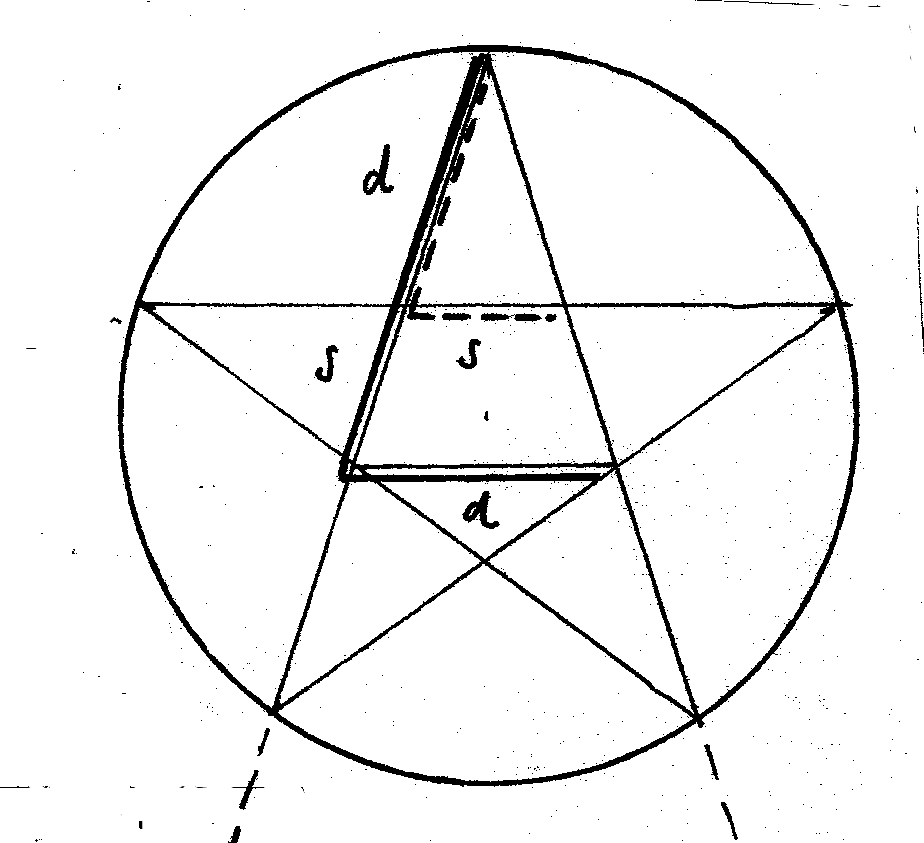
Nehmen wir ein Fünfeck (Pentagon), einen darin eingeschriebenen Fünfstern (Pentagramm), und das sich in dessem Inneren ergebende kleinere Fünfeck:
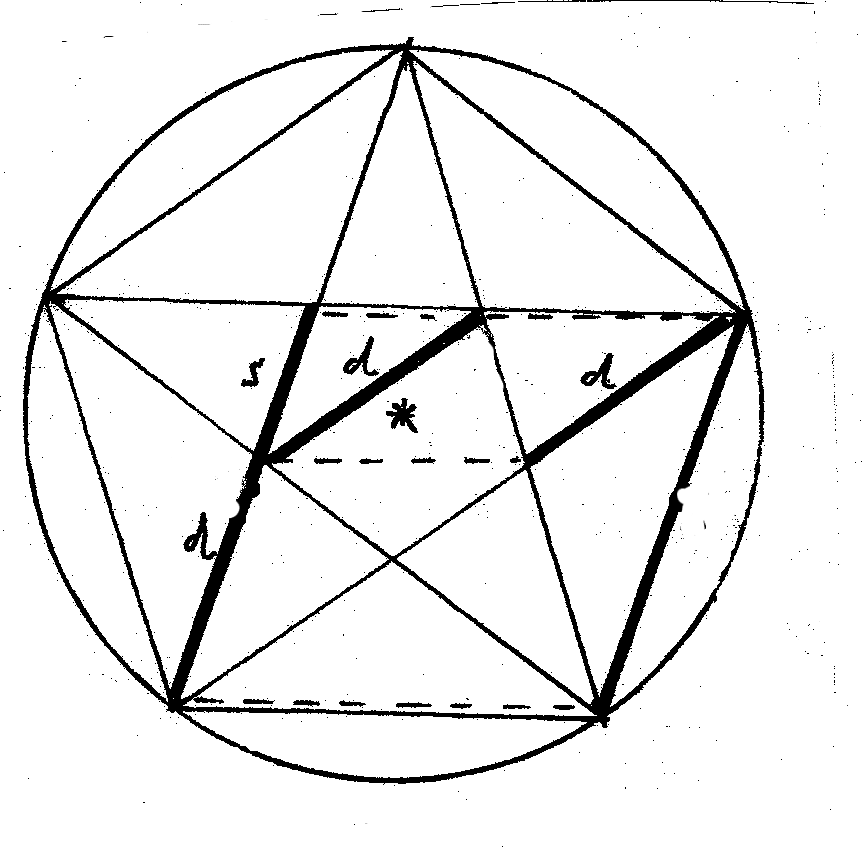
Pentagon und Pentagramm
Aus der Symmetrie des regelmäßigen Fünfecks folgt anschaulicherweise die Parallelität von Seite und gegenüberliegender Diagonale. Denn beide schneiden die Symmetrieachse im rechten Winkel, sind also parallel.
Daraus folgt auch die Parallelität der entsprechenden Diagonalen von äußerem und innerem Fünfecks.
Aus dieser Eigenschaft folgt ein Parallelogramm, das zeigt, daß die "Zackenlänge" des Pentagramms der Diagonale des inneren Pentagons gleich ist. ( $d = d$ ).

Aus der Anwendung des Zweiten Strahlensatzes (siehe Anhang) folgt aus der nächsten Zeichnung unmittelbar
d/s = (d+s) / d
q.e.d. !

Goldener Schnitt im Pentagramm"

2.2 Die Irrationalität des Goldenen Schnittes

"Irrational" ist das Verhältnis zweier Größen, die kein "gemeinsames Maß" haben.
Das seit ca. 400 vor Chr. belegte Verfahren zum Auffinden des gemeinsamen Maßes ist die "Wechselwegnahme", welche (vereinfacht!) so funktioniert:
Man ziehe von der größeren die kleinere ab und betrachte die kleinere und den entstehenden Rest.
Sind diese beiden Größen gleich, so entsprechen diese dem gesuchten gemeinsamen Maß der Ausgangsgrößen.
Bei Ungleichheit ziehe man wiederum die nun kleinere von der nun größeren ab und setze das Verfahren bis zum Erfolge fort.

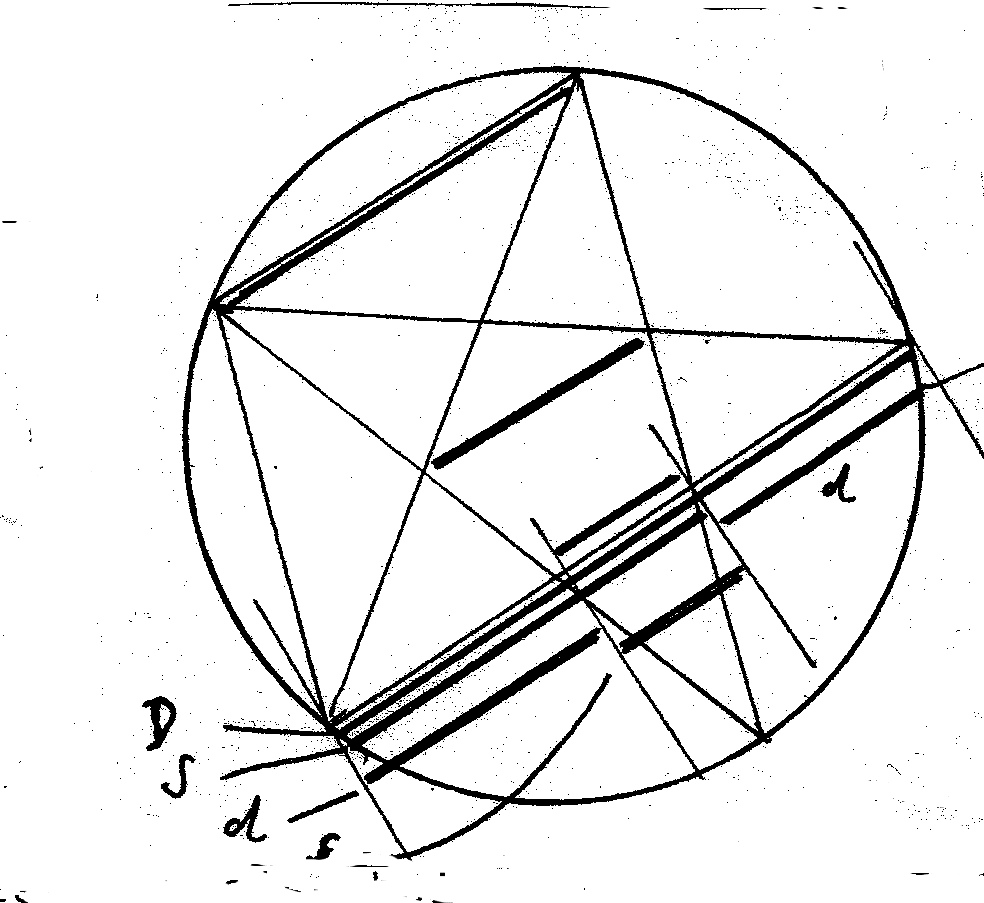
Nimmt man nun aber von der großen Diagonale D (siehe folgendes Bild) die große Seite S weg, so erhält man die Zackenlänge d. Nimmt man diese wiederum von der Seite weg (S-d), so erhält man die Seite des kleinen Fünfecks (s).

Nach zwei Schritten der Wechselwegnahme sind wir also bei zwei Größen angekommen (Zackenlänge=Diagonale des kleinen Fünfecks=d, und Seite des kleinen Fünfecks=s), die (natürlich verkleinert) in genau demselben Verhältnis stehen wie die Ausgangsgrößen (d/s = D/S) !

Niemals bei beliebig häufiger Fortsetzung werden wir deshalb zwei gleiche Größen und damit ein gemeinsames Maß finden, der GS ist also irrational!

Wechselwegnahme im Pentagramm q.e.d. !

2.3 Symbolfunktion des Pentagramms

Obwohl auch Kreis und Quadrat irrationale, "nicht-aufschreibbare", "über-zählbare" Proportionen beinhalten, ist gerade das Pentagramm oft abergläubischerweise mit dem Zauberkräftigen und Bösen identifiziert worden.

Kulturdruck und Triebangst haben das Grenzenlose mit dem Bösen identifiziert.

Das Pentagramm nun zeichnet sich Kreis und Quadrat gegenüber dadurch aus, daß, hat man das Irrationale einmal erkannt, es einen bei jeder Betrachtung erneut förmlich anspringt.

3 Unendliche Folge von Verkleinerungen und ihre Summe

Setzen wir ausgehend von einer Größe "e" das Verkleinern im Verhältnis des GS. (also das Abziehen des Kleineren vom Größeren) immer weiter fort, so erhalten wir eine unendliche geometrische (exponentielle) Folge, welche beliebig klein werden kann.
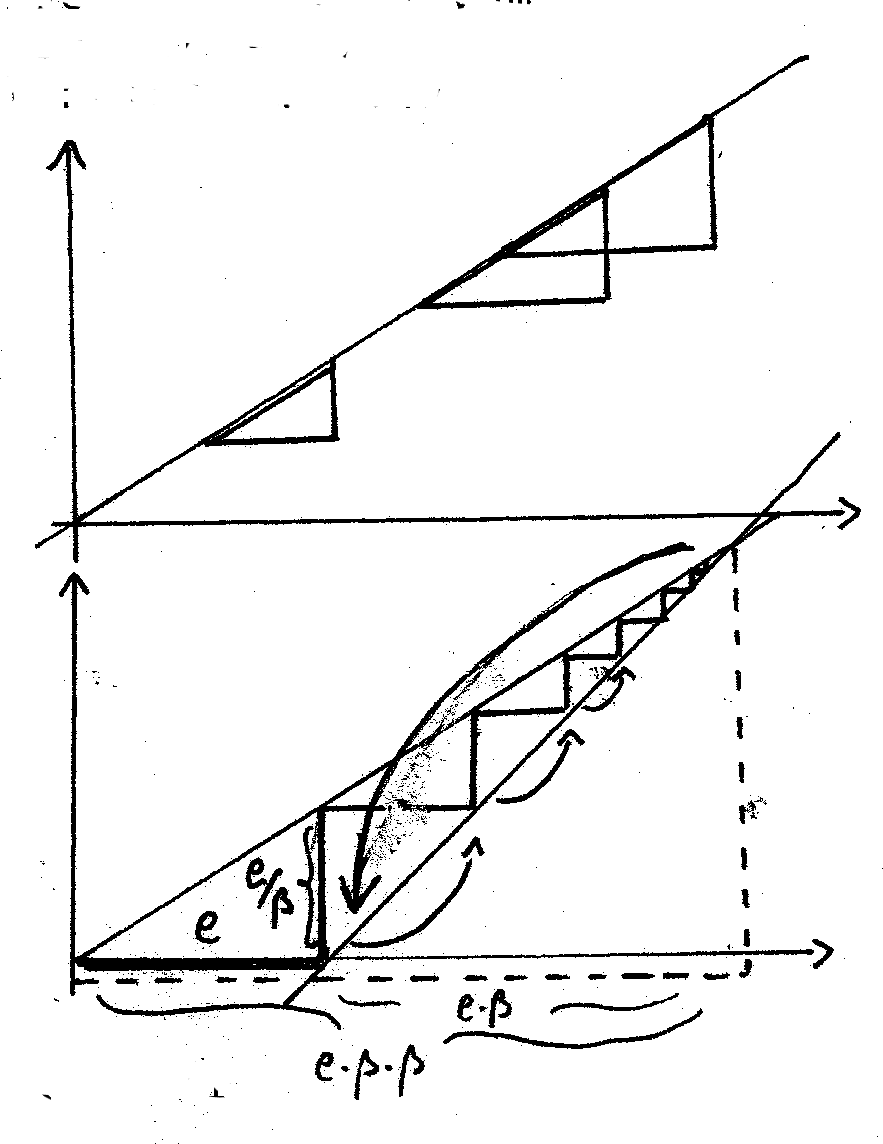
Die durch den Ursprung gehende Grade in der nächsten Zeichnung repräsentiert die Funktion y=(l/ß)x.
Die zu den Achsen parallelen Katheten aller Dreiecke, deren Hypothenuse auf dieser Geraden liegen, stehen also im Verhältnis des GS.
Gehen wir nun aus von unserem "e", so finden wir mittels eines solchen Dreiecks den Wert (l/ß)*e. Mit Hilfe einer zweiten Geraden (y = x-e) klappen wir diese Strecke zurück in die Horizontale und suchen wiederum den G.S., also (1/ß)*(1/ß)*e.

Wiederholen wir dies unendlich oft, so erreichen wir den Schnittpunkt beider Geraden, welcher also die Summe unserer unendlichen Folge von kleiner werdenden Werten darstellt.

Da auch das gestrichelte "Summendreieck" dem G:S.folgen muß, sehen wir:
Die Summe aller Verkleinerungen von e im G.S.-Verhältnis ist gleich der Vergrößerung im G.S.-Verhältnis!
Unendliche Folge und Summe davon

Dasselbe ergebnis gibt sich auch durch die algebraische Formel für die Summe von geometrischen Reihen, wenn der Faktor kleiner als eins ist:

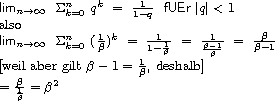
Die Summenformel der fortgesetzten Teilung im Goldenen Schnitt

4 Bedeutung des G.S. in der Musik

4.1 Gegengewicht zu den "Kleinen Ganzen Zahlen"

Bedeutung hat die Verwendung des GS im Werke Bachs (und anderer!) zunächst einmal auf der Ebene des Materials, dann aber auch im Gehalt:

Im Material bedeutet das irrationale Verhältnis des GS zunächst ein dringend benötigtes Gegengewicht zu der auf der Additions (und Division) kleiner ganzer Zahlen beruhenden Gestaltung auf rhythmischer und metrischer Ebene.
Zwar können irrationale Verhältnisse im rationalen System musikalischer Metrik immer nur annäherungsweise repräsentiert werden, sie verweisen aber auf eine Regeldefinition, die ihrem Wesen nach auf Irrationalität beruht (natürlich nur im mathematischen Wortgebrauch!) und damit das Mechanisch-Abzählbare transzendiert zum organisch-Wuchernden.

Dies ist in gewisser Weise auch eine Parallele zu den verschiedenen Stimmungssystemen, die Bach ja durchaus voraussetzte, und die endlich bis zur "12ten Wurzel aus 2" sich differenzierten.

4.2 Transzendierender Formteilrhythmus

Für den trans-musikalischen Gehalt müssen wir etwas weiter ausholen:
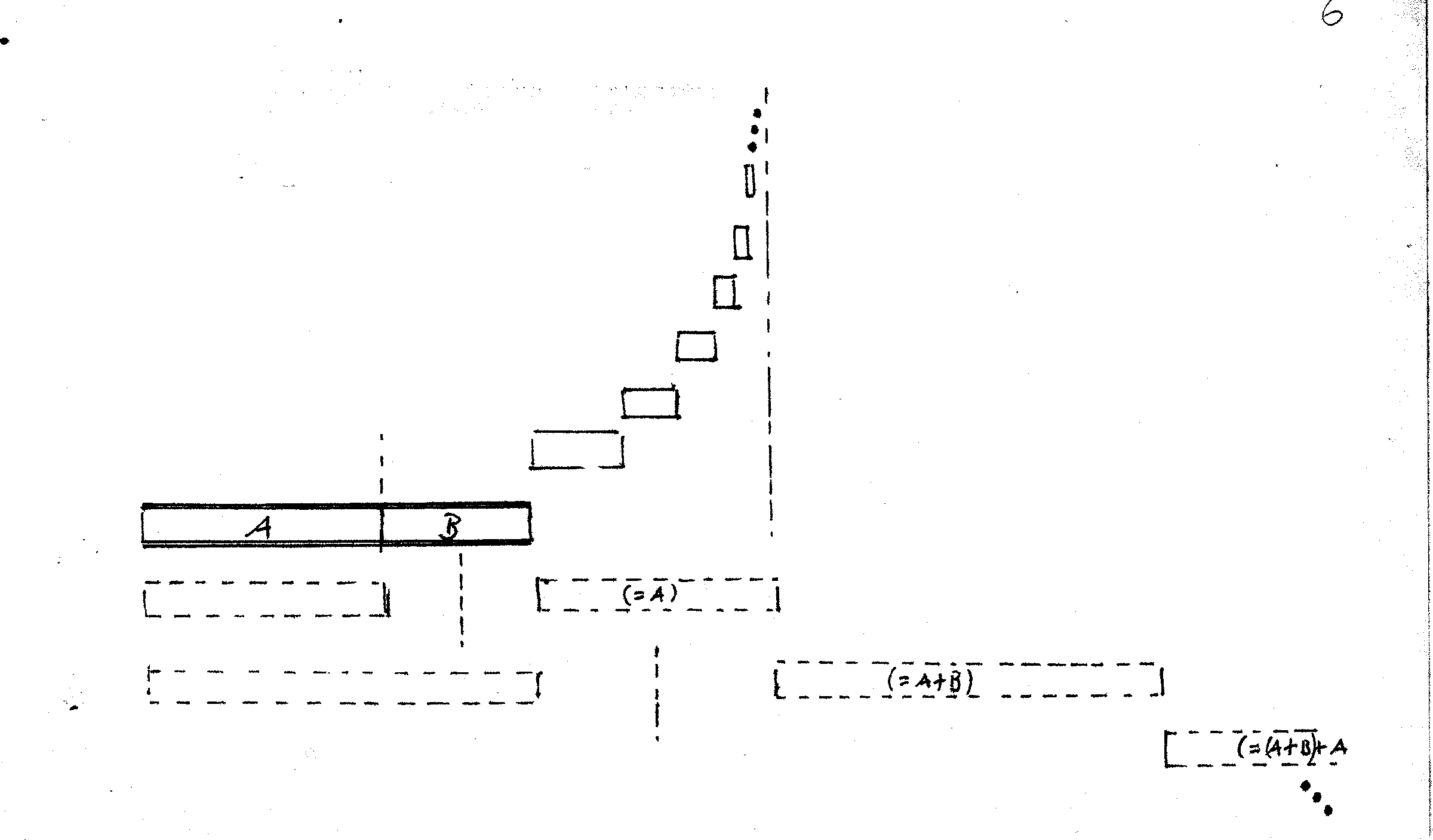
Einer Bach'schen Fuge wie jedem anderen Werk, welches im Verhältnis des GS. in zwei Teile (A+B) gegliedert ist, wobei A der längere, ist das "Mitkomponieren der Nachzeit" allemal immanent:
Das Nachschwingen im Hörer induziert nämlich (kann induzieren) eine unendliche Welle von immer kürzer werdenden Dauernempfindungen. Diese nähern sich einer (zugleich konkreten wie imaginären) Grenze zunehmend an, ohne sie je zu erreichen.

Die Gesamtdauer dieser sich verkleinernden Welle wiederum entspricht (nach dem oben zur Summe des Grenzwertes Gesagtem, und wie sichtbar in folgender Zeichnung) der des ersten Formteils (A), so daß (quasi aus dem Rücklauf der Proportionen) eine zweite unendliche Welle entsteht, - diese sich im GS. vergrößernd bis in alle Ewigkeit.

Die zuvörderst erkennbare Bedeutung ist eine rein naturphilosophische:
Das in dieser Interpretation aufscheinende Weltbild ist das eines "allüberall verknüpften Kosmos" .
Ein Musikstück ist ein Stein, den ich in den Teich der Welt werfe; die Wellen, die er verursacht, mögen sich bis Unkenntlichkeit stetig verkleinern, - aufhören werden sie nie. Keine Tat ist reversibel; wenn sie auch (auf der Ebene der Modellbildung) nicht mehr "Ursache" sein kann, so ist sie doch dem "Ding" zugefügt und damit auf ewig eigen.
Unendliches Nachklingen eines Musikstücks

Noch weitergehend könnte man die sich exponentiell verkürzenden Dauernfolgen als eine Veranschaulichung ("Veranhörlichung") des ewigen Lebens auffassen:
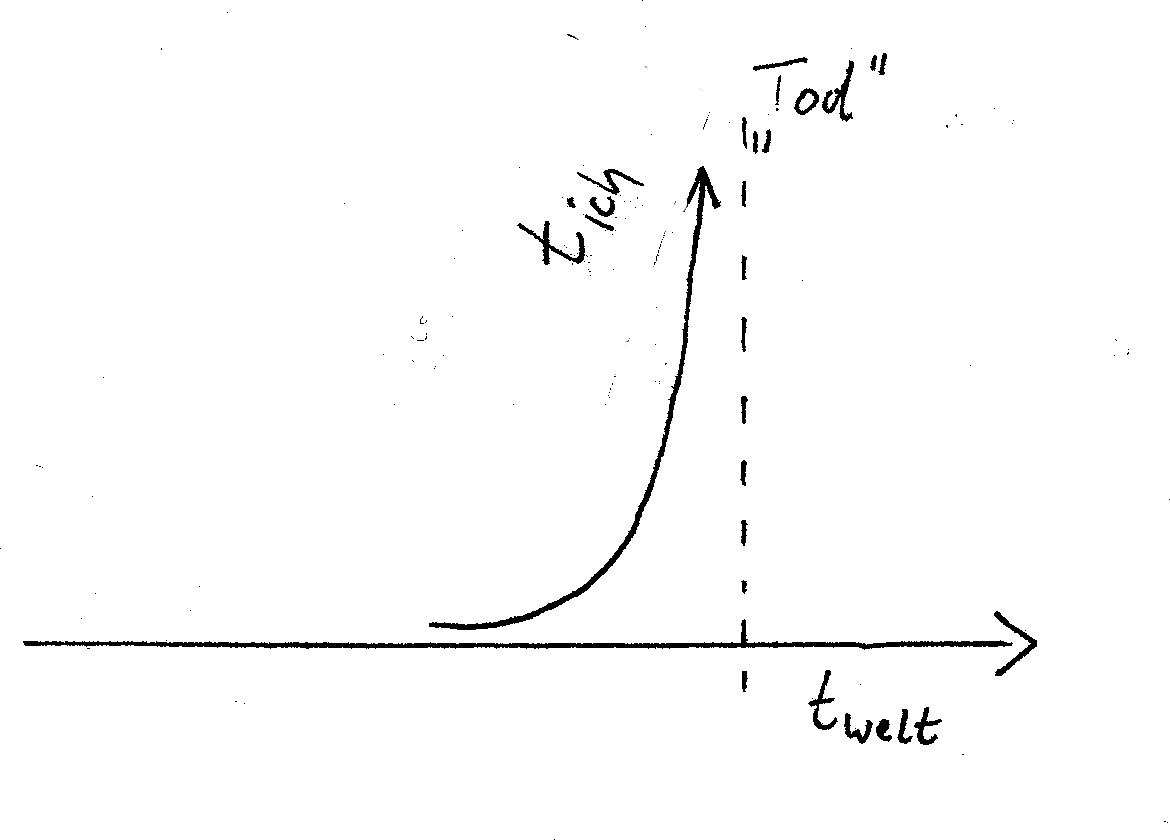
Die wirk-liche Zeit des Individuums (t_Ich) koppelt sich im Vorgang des Sterbens ab von der Zeit der anderen (t_Welt), um in ihre eigene Ewigkeit einzugehen. Die Asymptote meiner eigenen Zeit ist das, was von außen betrachtet scheinbar der Tod ("Hirntod" ?) ist.
Der zurückbleibenden Welt aber bleibt die Aufgabe, in immer größeren Schritten ihrem eschatologischen Ziel zuzustreben.
Trennung der Zeit von Ich und Welt

Volute

5 ANHANG --- Zur Auffrischung: die Strahlensätze

Seien d, e, und f Geraden, die durch einen gemeinsamen Punkt P gehen, und g und h zueinander parallele Geraden, die beide diese Geraden schneiden. So gelten für die verschiedenen entstehenden Abschnitte (k bis r) verschiedene Verhältnisgleichungen.

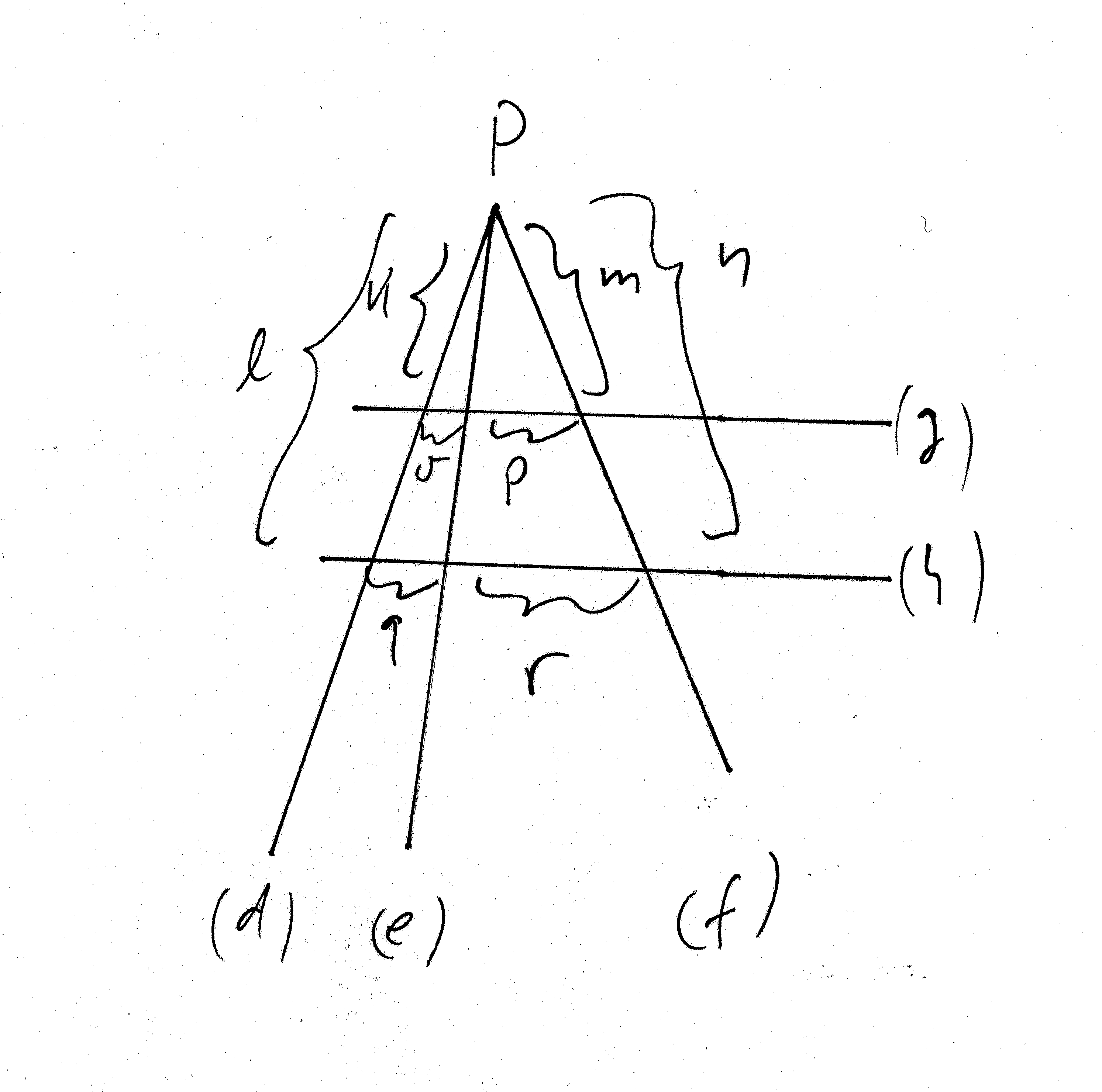
Die drei Strahlensätze und ihre Anwendung auf diese Zeichnung lauten:
"Erster Strahlensatz" :
Die Abschnitte auf den Strahlen stehen in gleichem Verhältnis:
k/l = m/n, also auch k/m = l/n
"Zweiter Strahlensatz"
Die Abschnitte auf den Parallelen verhalten sich wie die auf den Strahlen:
o/q = k/l, also auch o/k = q/l
"Dritter Strahlensatz"
Die Abschnitte auf den Parallelen verhalten sich gleich
o/p = q/r, also auch o/q = p/r

Das klingt nach dröger Mittelstufengeometrie. Tatsächlich aber sind es nur allgemeine Formulierungen alltäglicher Schlußfolgerungen, die unserer Vernunft als unbedingt notwendig sofort einleuchten. Mehr noch, sie werden von unserem Verstand (beides entnommen der Schopenhauerschen Sprachregelung) täglich dutzendfach angewandt, ohne daß wirs unbedingt merken.

Und nicht nur von uns! Schon der Verstand des Tieres weiß, daß ein ferner Feind zwar klein aussieht, aber gefährlich schnell näher kommen kann und dabei größer wird, und das eine ferne Beute nicht weniger nahrhaft ist, nur weil sie kleiner aussieht!

© senzatempo.de     markuslepper.eu        2016-03-08_10h31
produced with eu.bandm.metatools.d2d    and    XSLT
music typesetting by musixTeX    and    LilyPond